马氏体相变及形状记忆合金.ppt

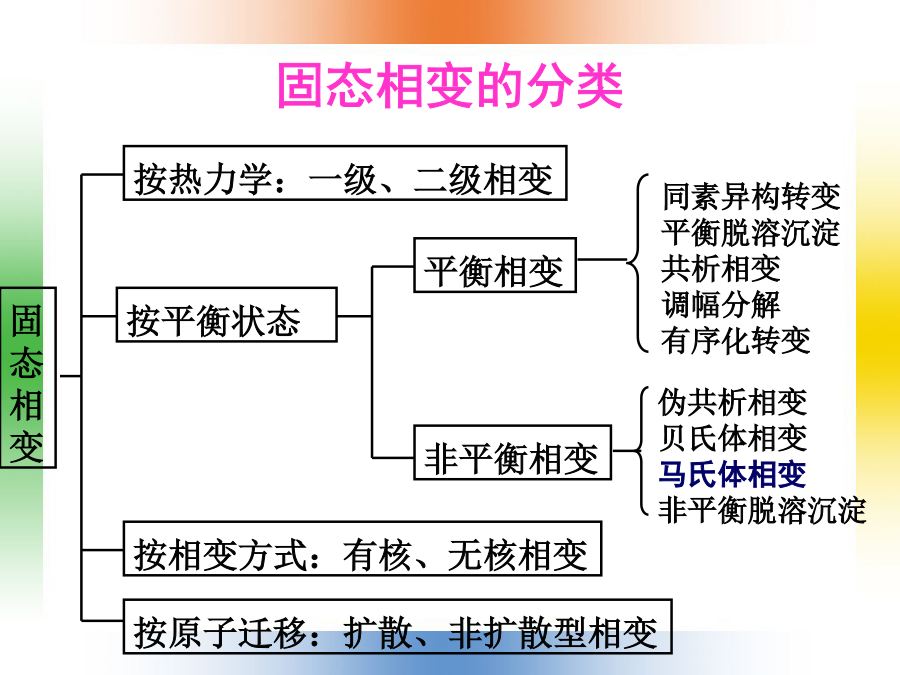
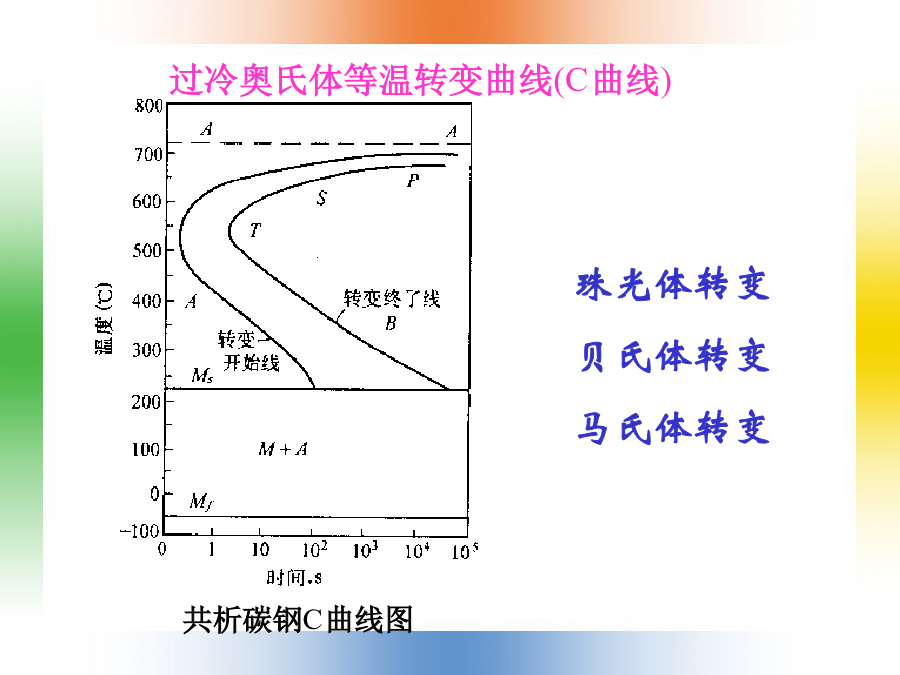
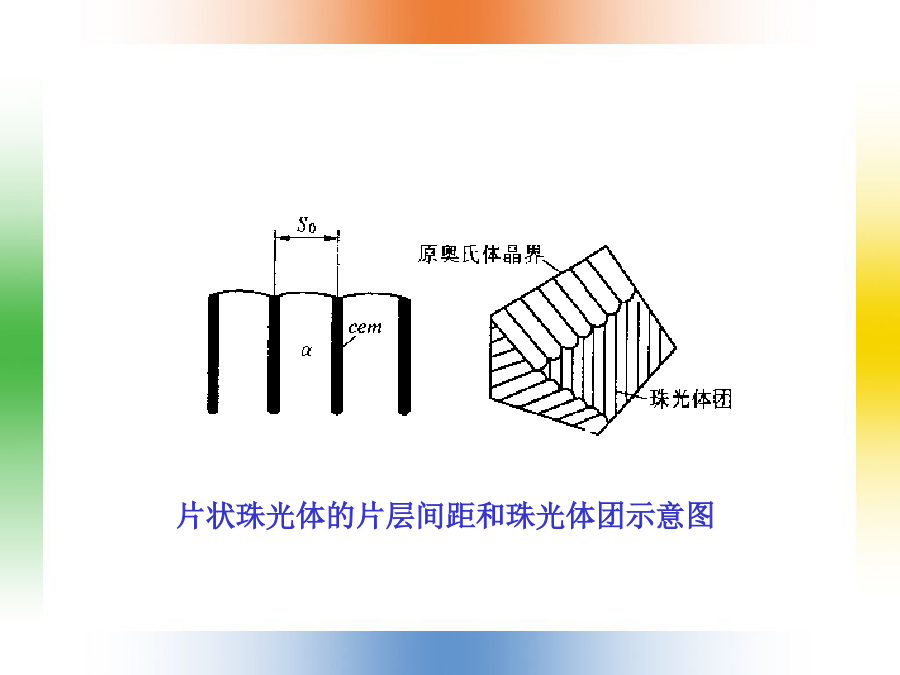
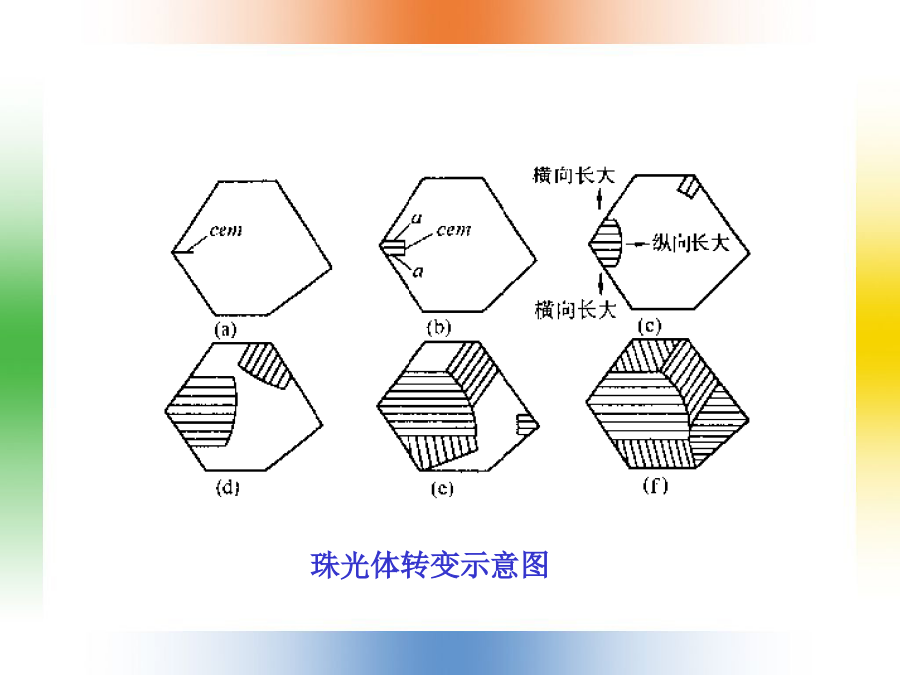
内容固态相变的分类4.1马氏体相变钢：含碳量小于2％并含有某些其他元素的铁碳合金。
合金：指由两种或两种以上的金属或金属与非金属经熔炼、烧结或其他方法组合而成并具有金属特性的物质。组成合金的基本的独立的物质称为组元。组元可以是金属和非金属元素，也可以是化合物。固态下所形成的合金相基本上可分为固溶体和中间相两大类。
固溶体：是以某一组元为溶剂，在其晶体点阵中溶人其他组元原子（溶质原子）所形成的均匀混合的固态溶体，它保持着溶剂的晶体结构类型。分为置换固溶体和间隙固溶体两种。铁的两种晶体结构：
体心立方结构（存在于两个温度范围内，912℃以上称α铁，1394℃以上称δ铁）；
面心立方结构（存在于912～1394℃之间，称γ铁）
碳在钢中的两种主要存在形式：
溶入铁中与铁形成固溶体；
另一是与铁形成铁碳化合物，称渗碳体（Fe3C）。
碳溶于α铁中形成的固溶体称铁素体；溶于γ铁中形成的固溶体称奥氏体，其最大溶解度为2.11％。共析碳钢C曲线图共析转变（珠光体转变）片状珠光体的片层间距和珠光体团示意图珠光体转变示意图马氏体转变的发展过程十九世纪未到二十世纪初主要局限于研究钢中的马氏体转变及转变所得产物—马氏体。
二十世纪三十年代，人们用X射线结构分析的方法测得钢中马氏体是碳溶于α-Fe而形成的过饱和固溶体，马氏体中的固溶碳即原奥氏体中的固溶碳，因此，曾一度认为“所谓马氏体即碳在α-Fe中的过饱和固溶”。
曾经有人认为“马氏体转变与其它转变不同，是一个由快冷造成的内应力场所引起的切变过程”。
四十年代前后，在Fe-Ni、Fe-Mn合金以及许多有色金属及合金中也发现了马氏体转变。不仅观察到冷却过程中发生的马氏体转变；同时也观察到了在加热过程中所发生的马氏体转变。由于这一新的发现，人们不得不把马氏体的定义修定为：“在冷却过程中所发生马氏体转变所得产物统称为马氏体”。把以晶格畸变为主的位移型无扩散相变统称为马氏体相变。马氏体转变的主要特性
（一）马氏体转变的非恒温性
马氏体转变有一上限温度，这一温度称为马氏体转变的开始温度，也称为马氏体点，Ms表示。不同的材料Ms是不同的。
马氏体转变还有一个下限温度，用Mf，当奥氏体过冷到Mf以下时转变也不能再进行了。称为马氏体转变的下限温度或马氏体终了点。也就是说马氏体转变是在Ms—Mf之间进行的。
一般钢材的Mf都低于室温，在生产中为了获得更多的马氏体，常采用深冷到室温以下的处理工艺，这种工艺方法称为冷处理。（二）马氏体转变的切变共格和表面浮凸现象
马氏体转变时能在预先磨光的试样表面上形成有规则的表面浮凸。这说明马氏体的形成与母相奥氏体的宏观切变密切相关。下图是三种不变平面应变，图中的C既有膨胀又有切变，钢中马氏体转变即属于这一种。（三）马氏体转变的无扩散性
马氏体转变只有点阵改组而无成份变化，转变时原子做有规律的整体迁移，每个原子移动的距离不超过一个原子间距，且原子之间的相对位置不发生变化。
1、一些具有有序结构的合金发生马氏体转变后有序结构不发生变化；
2、Fe-C合金奥氏体向马氏体转变后，C原子的间隙位置保持不变；
3、马氏体转变可以在相当低的温度范围内进行，且转变速度极快。例如：Fe-C、Fe-Ni合金，在-20~-196℃之间一片马氏体形成的时间约5×10-5─5×10-7秒。（四）马氏体转变的位向关系及惯习面
奥氏体转变为马氏体时，新旧两相之间保持着严格的晶体学位向关系，马氏体的不变平面被称为马氏体的惯习面，以平行于此面的母相的晶面指数表示。
（五）马氏体转变的可逆性
冷却时高温相可以转变为马氏体，加热时马氏体可以逆转变为高温相，而且转变都是以马氏体转变方式进行的。与Ms—Mf相对应，逆转变有As—Af分别表示逆转变的开始和终了温度。马氏体转变的切变模型
M转变的无扩散性及在低温下仍以很高的速度进行等事实，都说明在相变过程中点阵的重组是由原子集体的、有规律的、近程迁动完成的，而无成份变化。因此，可以把M转变看作为晶体由一种结构通过切变转变为另一种结构过程。
自从1942年以来，由Bain开始，人们便根据M相变的特征，设想了各种相变机制。因为相变时母相发生明显的切变，所以早期提出的机制常常是从简单的切变过程推导出来的，企图通过简单的切变便可以得到与实验事实相符合的M。1、贝茵（Bain）模型
早在1942年Bain就注意到可以把面心立方点阵看成是轴比为c/a=1.41(即21/2:1)的体心正方点阵。同样，也可以把稳定的体心立方的铁素体看成是体心正方点阵，其轴比等于1。Bain模型给出了点阵变化的清淅的模型，但不能解释宏观切变和惯习面的存在，也不能解释M内部的亚结构。2、K—S切变模型
库尔久莫夫和萨克斯测出含C为1.4%的碳钢中M与A存在的位向关系，即K—S关系，为了满足这一取向关系必须有点阵的