可微函数类上的极值和最优恢复问题-豆柴文库

可微函数类上的极值和最优恢复问题.pptx

2024-10-06

20金币

329KB

24页

快乐****蜜蜂

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共24页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

可微函数类上的极值和最优恢复问题.pptx

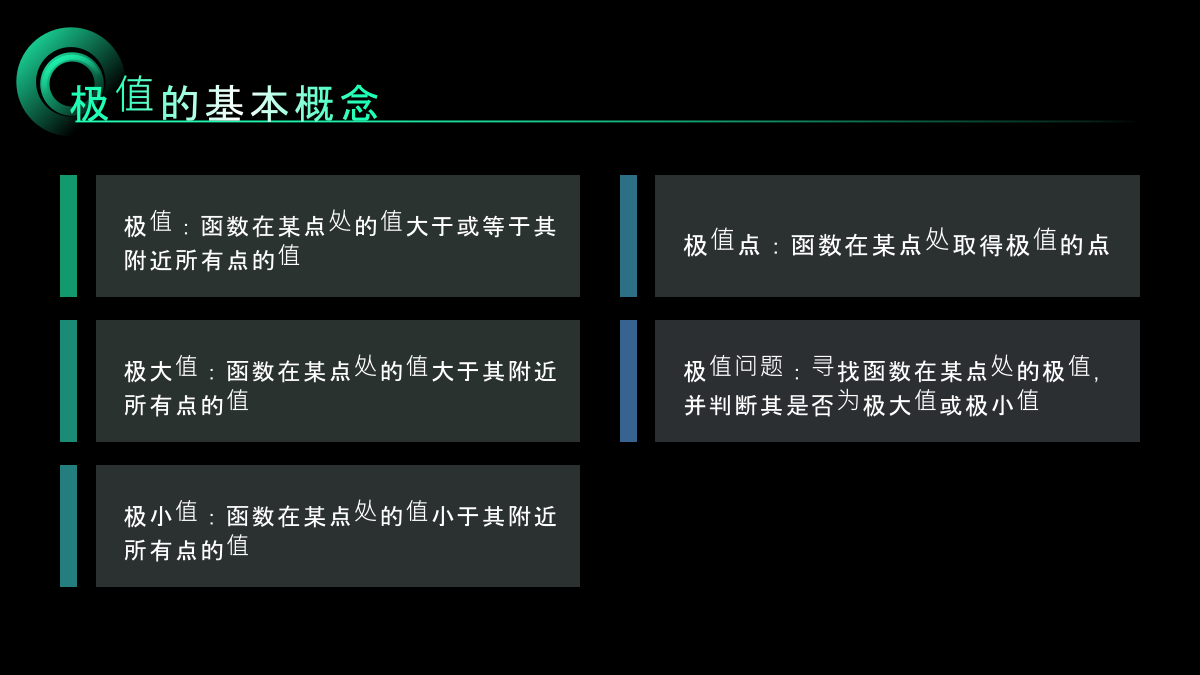
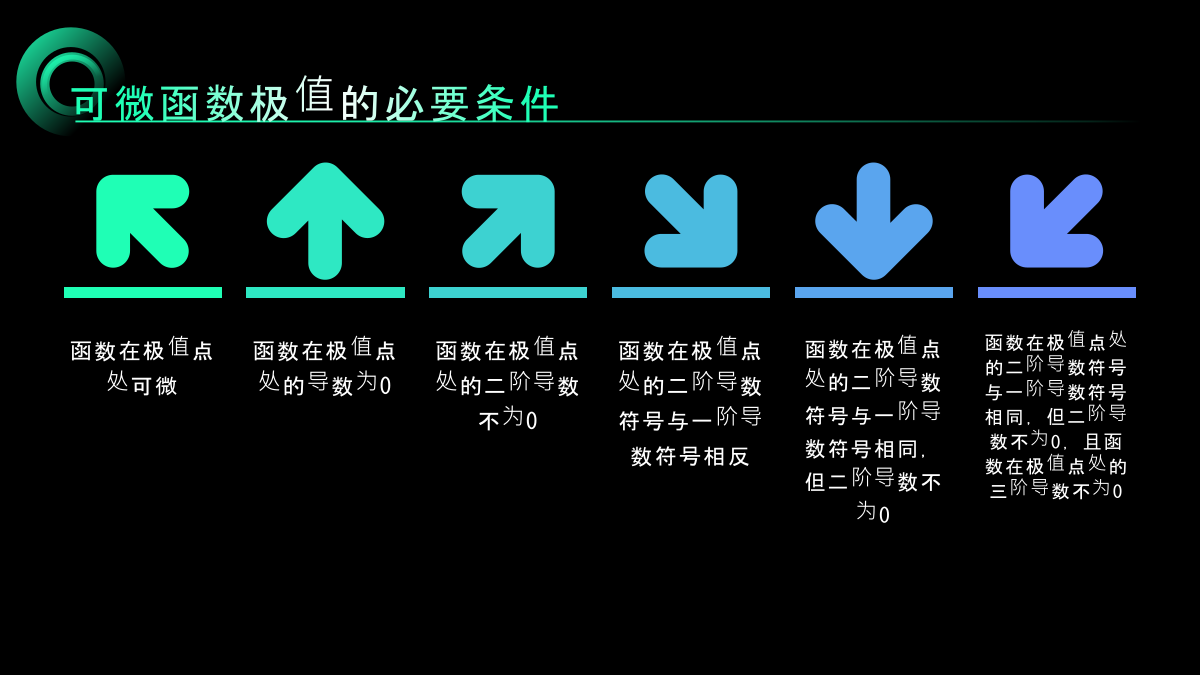
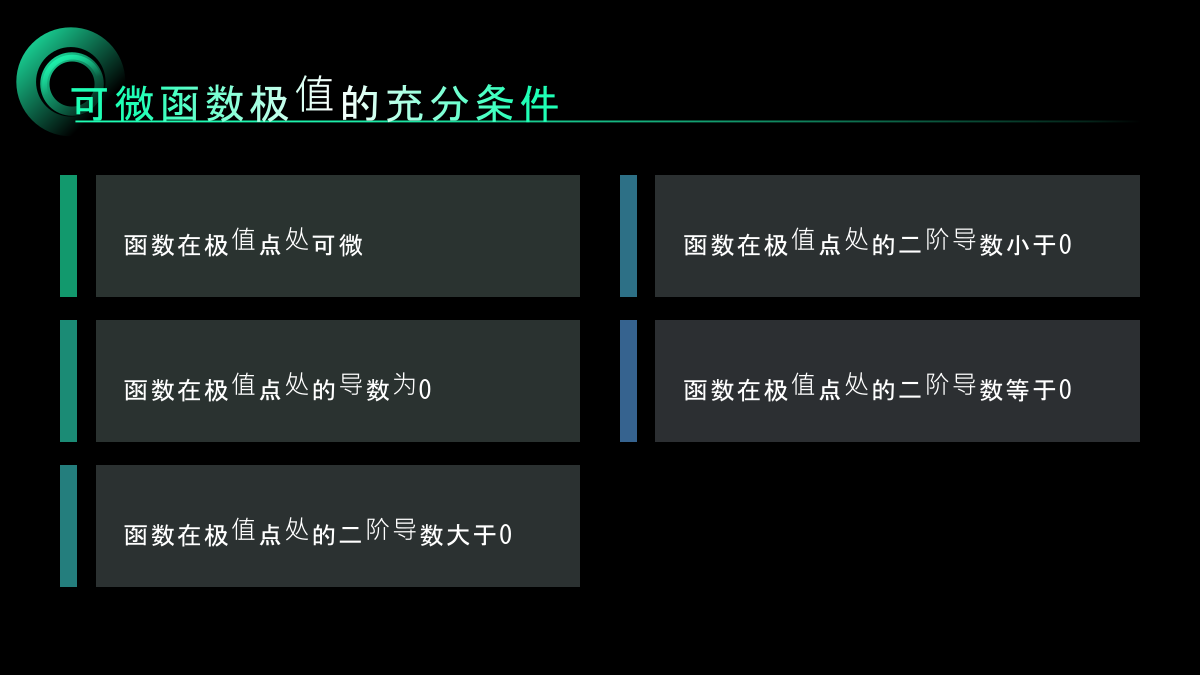
汇报人：CONTENTSPARTONEPARTTWO极值的基本概念可微函数极值的必要条件可微函数极值的充分条件极值的应用PARTTHREE最优恢复问题的定义和分类最优恢复问题的求解方法最优恢复问题的应用场景最优恢复问题的研究现状和未来发展PARTFOUR可微函数类上的极值和最优恢复问题的联系可微函数类上的极值和最优恢复问题的差异可微函数类上的极值和最优恢复问题在优化算法中的应用可微函数类上的极值和最优恢复问题在机器学习中的应用PARTFIVE可微函数类上的极值和最优恢复问题的研究难点和挑战可微函数类上的极

2024-10-06

329KB

α阶Lipschitz函数类上的最优恢复问题.docx

α阶Lipschitz函数类上的最优恢复问题标题:α阶Lipschitz函数类上的最优恢复问题摘要:最优恢复问题是在噪声影响下恢复原始信号的过程，他在统计和机器学习领域中具有重要的应用。本论文讨论α阶Lipschitz函数类上的最优恢复问题。首先介绍了最优恢复问题的定义和背景，接着给出α阶Lipschitz函数的定义和性质。然后，提出了一种能够有效解决α阶Lipschitz函数类上最优恢复问题的优化算法，并通过实验结果验证了算法的性能。1.引言最优恢复问题是恢复原始信号的过程，即通过观测数据和一些先验知识

2024-10-16

11KB

解析函数空间上的极值问题的开题报告.docx

解析函数空间上的极值问题的开题报告题目：解析函数空间上的极值问题一、选题背景解析函数是数学中的一类重要函数，具有很多优越的性质，比如连续、可导、可积等等。因此，在实际问题中，我们经常需要研究解析函数的性质，包括其在给定区域上的极值问题。在解析函数空间上的极值问题中，我们的目标是研究给定区域上解析函数的极值点和极值值。这是解析函数研究中的一个重要问题，对于许多应用都具有重要意义。二、研究内容和意义本课题研究内容涵盖如下几点：1.解析函数的基本概念和性质2.解析函数在有限点和无穷远处的极值问题3.解析函数在闭

2024-09-16

11KB

利用导数研究函数的极值和最值问题.docx

利用导数研究函数的极值和最值问题１．利用导数研究函数的极值的一般步骤：（１）确定函数的定义域．（２）求．（３）①若求极值，则先求方程的全部实根，再检验在方程根的左右两侧值的符号，求出极值．（当根中有参数时，要注意讨论根是否在定义域内）②若已知极值大小或存在情况，则转化为已知方程的根的大小或存在情况，从而求解．２．求连续函数在上的最大值与最小值的步骤：（１）求函数在内的极值；（２）将函数的各极值与端点处的函数值，比较，其中最大的一个是最大值，最小的一个是最小值.例1.(2018北京,18,13分)设函数.(

2024-11-04

140KB

一类生产函数的最优化问题.docx

一类生产函数的最优化问题标题：最优化问题：关于一类生产函数的研究引言：经济发展是一个重要的课题，而生产函数作为经济增长理论的基础，对于经济学家和政策制定者来说具有重要的意义。生产函数描述了输入和输出之间的关系，研究最优化问题可以帮助我们找到生产要素的最佳配置，从而实现经济的高效和可持续发展。本文旨在探讨一类生产函数的最优化问题，并分析其在实际经济中的应用。第一章：最优化理论的基本概念和方法本章主要介绍最优化理论的基本概念和方法，包括目标函数、约束条件、最优化问题的分类等。引入拉格朗日乘数法、线性规划等常用

2024-10-18

10KB