【数学】222《用样本的数字特征估计总体的数字特征2》课件(新人教B版必修3).ppt

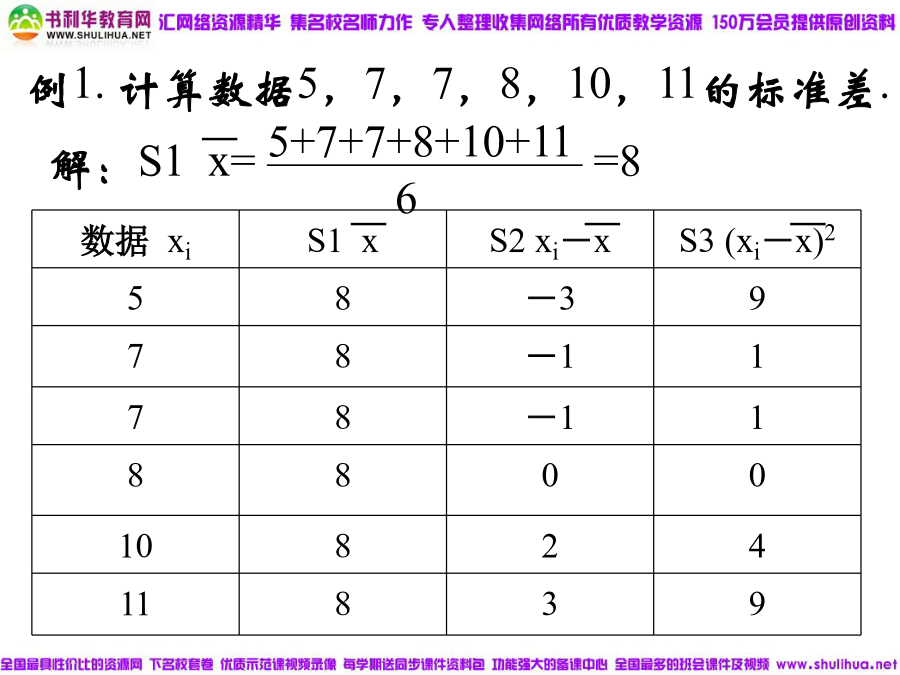
2.2.2用样本的数字特征估计总体的数字特征（二）二、用样本的标准差估计总体的标准差（1）方差：设在一组数据，x1，x2，…，xn中，各数据与它们的平均数x的差的平方分别是（2）标准差：我们把数据的方差的算术平方根叫做这组数据的标准差，它也是一个用来衡量一组数据的波动大小的重要的量。S3算出（i=1，2，…，n）；例1.计算数据5，7，7，8，10，11的标准差.S4s2=———————=4；例2.从某灯泡厂生产的一批灯泡中随机地抽取10只进行寿命测试，得数据如下（单位：h）:
1458，1395，1562，1614，1351，1490，1478，1382，1536，1496
使用函数型计算器或计算机的Excel软件求样本的平均数x和样本的标准差。解：按键解2：打开Excel工作表，在一列输入数据，如将10个数据输入A1到A10单元格中.
（1）利用求和∑计算它们的和；
（2）用函数AVERAGE(A1:A10)求它们的平均数；
（3）用函数VARPA(A1:A10)求它们的方差；
（4）用开方函数Sqrt(方差)计算它们的标准差.例3.计算数据89，93，88，91，94，90，88，87的方差和标准差。（标准差结果精确到0.1）例4.从甲、乙两名学生中选拔一人乘积射击比赛，对他们的射击水平进行测试，两人在相同的条件下各射击10次，命中环数如下﹕
甲﹕7，8，6，8，6，5，8，10，7，4；
乙﹕9，5，7，8，7，6，8，6，7，7.
（1）计算甲、乙两人射击命中环数的平均数和标准差；
（2）比较两人的成绩，然后决定选择哪一人参赛.解：（1）计算得x甲=7，x乙=7；
s甲=1.73，s乙=1.10.（3）标准差和频率直方图的关系再看钢管内径尺寸的例子，它的样本平均数是25.401，样本标准差是0.056，再直方图中用虚线标出平均数所在的位置，并画出距平均数两侧各一倍标准差和两倍标准差的区间。可以看到大约有70%的钢管内径尺寸落在距平均数两侧各一倍标准差的区间内，即(x－s,x+s)
大约有95%的钢管内径尺寸落在距平均数两侧各两倍标准差的区间内，即(x－2s,x+2s)。s的平均数为，练习：A（7）在一次歌手大奖赛上，七位评委为歌手打出的分数如下：9.4，8.4，9.4，9.9，9.6，9.4，9.7，去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为________1．甲、乙两种水稻试验品种连续5年的平均单位面积产量如下（单位：t/hm2），试根据这组数据估计哪一种水稻品种的产量比较稳定。乙品种的样本平均数也为10，样本方差为[(9.4－10)2+(10.3－10)2+(10.8－10)2+(9.7－10)2+(9.8－10)2]÷5=0.24.
因为0.24>0.02，
所以，由这组数据可以认为甲种水稻的产量比较稳定。2．为了保护学生的视力，教室内的日光灯在使用一段时间后必须更换。已知某校使用的100只日光灯在必须换掉前的使用天数如下，试估计这种日光灯的平均使用寿命和标准差。解：各组中值分别为165，195，225，285，315，345，375，由此算得平均数约为故所求的标准差约（天）