张量分解学习.ppt

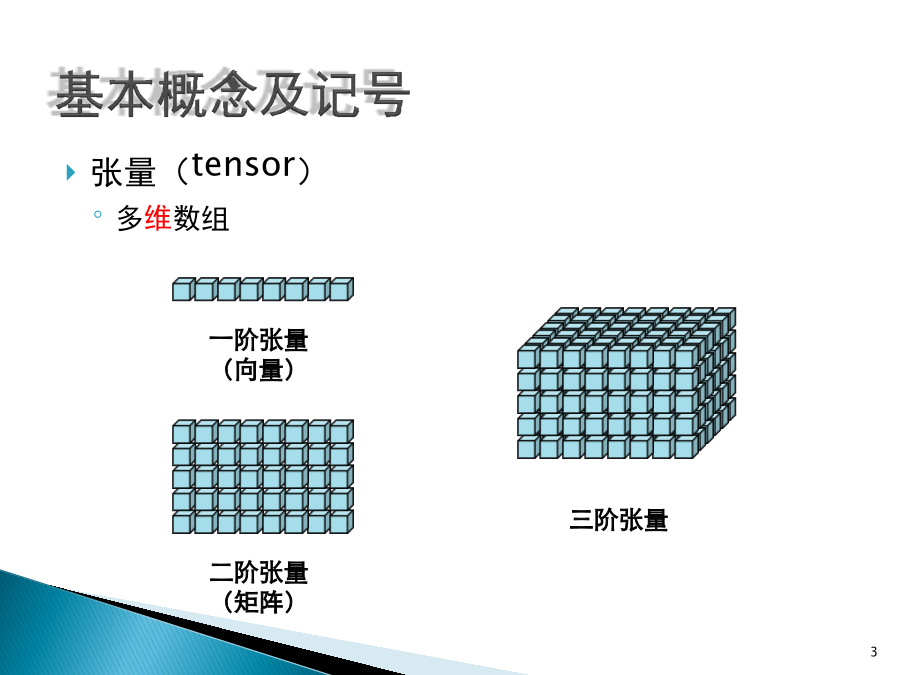
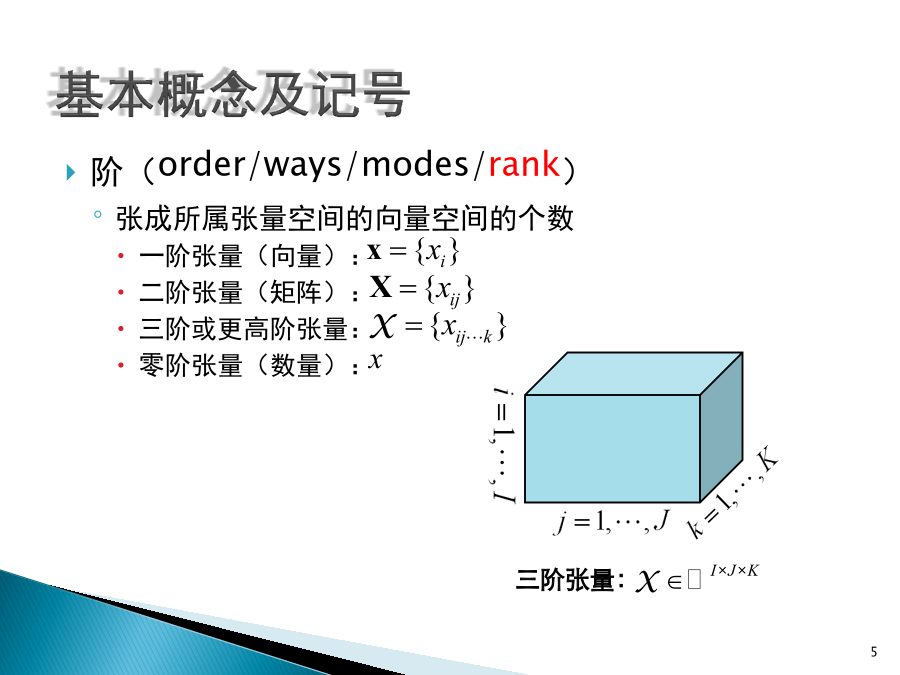
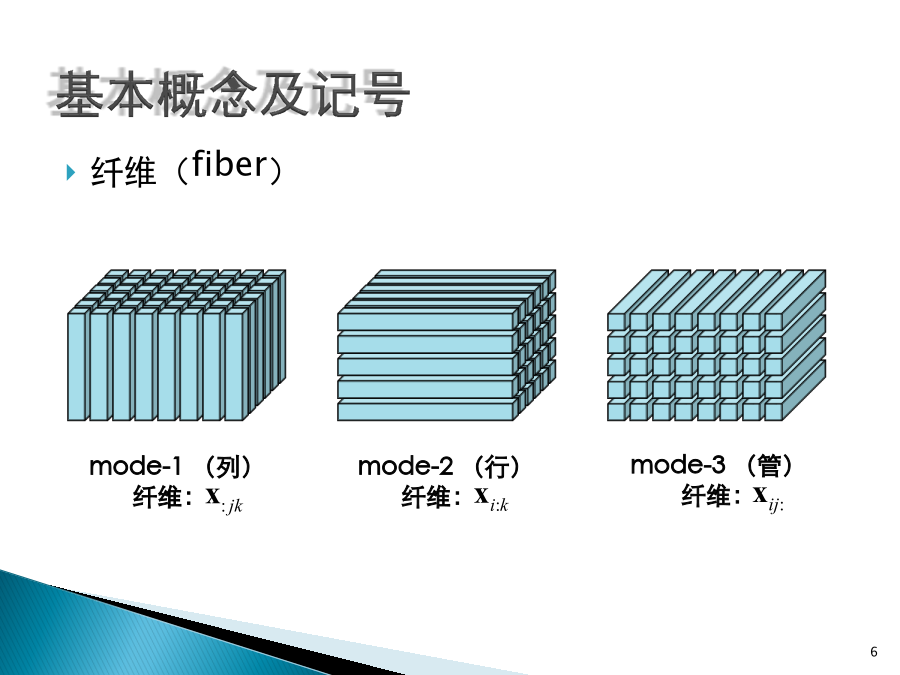
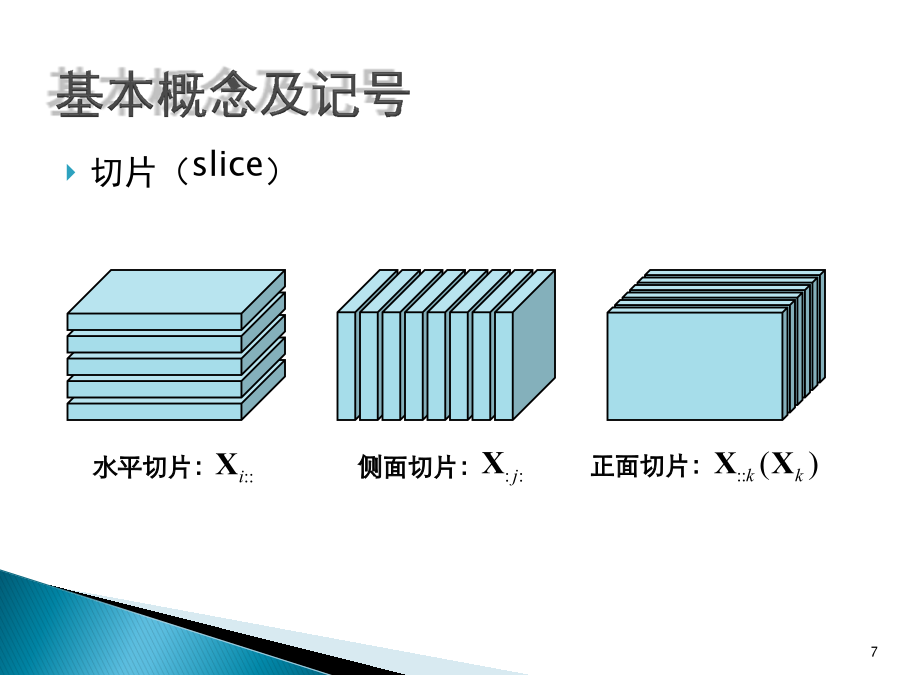
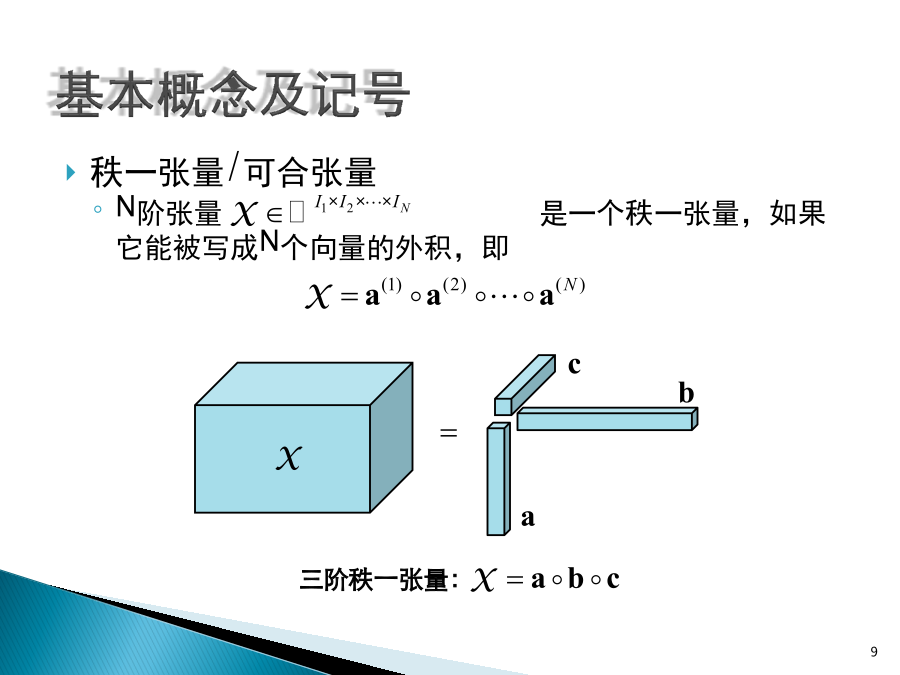
张量分解基本概念及记号
张量（tensor）
多维数组张量空间
由若干个向量空间中的基底的外积张成的空间阶（order/ways/modes/rank）
张成所属张量空间的向量空间的个数
一阶张量（向量）：
二阶张量（矩阵）：
三阶或更高阶张量：
零阶张量（数量）：纤维（fiber）切片（slice）内积和范数
设
内积：

（Frobenius）范数：秩一张量/可合张量
N阶张量是一个秩一张量，如果它能被写成N个向量的外积，即（超）对称和（超）对角
立方张量：各个mode的长度相等
对称：一个立方张量是对称的，如果其元素在下标的任意排列下是常数。如一个三阶立方张量是超对称的，如果

对角：仅当时，
展开（matricization/unfolding/flattening）
将N阶张量沿mode-n展开成一个矩阵n-mode（矩阵）乘积
一个张量和一个矩阵的n-mode乘积，其元素定义为

这个定义可以写成沿mode-n展开的形式

性质：n-mode（向量）乘积
一个张量和一个向量的n-mode乘积，其元素定义为

性质：

矩阵的Kronecker乘积
，则

性质：矩阵的Kronecker乘积
矩阵的Kronecker积还和张量和矩阵的n-mode乘积有如下关系矩阵的Khatri-Rao乘积
，则

性质：
矩阵的Hadamard乘积
，则

性质：CP分解
CP分解的其他名字
PolyadicFormofaTensor,Hitchcock,1927
PARAFAC(ParallelFactors),Harshman,1970
CANDECOMP/CAND(Canonicaldecomposition),Carroll&Chang,1970
TopographicComponentsModel,Möcks,1988
CP(CANDECOMP/PARAFAC),Kiers,2000CP分解的张量形式
将一个张量表示成有限个秩一张量之和，比如一个三阶张量可以分解为CP分解的矩阵形式
因子矩阵：秩一张量中对应的向量组成的矩阵，如

利用因子矩阵，一个三阶张量的CP分解可以写成展开形式带权CP分解
为了计算方便，通常假设因子矩阵的列是单位长度的，从而需要引入一个权重向量，使CP分解变为

对于高阶张量，有

其展开形式为张量的秩和秩分解
张量的秩定义为用秩一张量之和来精确表示所需要的秩一张量的最少个数，记为

秩分解：

可见秩分解是一个特殊的CP分解，对应于矩阵的SVD

目前还没有方法能够直接求解一个任意给定张量的秩，这被证明是一个NP-hard问题
张量的秩
不同于矩阵的秩，高阶张量的秩在实数域和复数域上不一定相同。例如一个三阶张量

在实数域内进行秩分解得到的因子矩阵为

而在复数域内进行分解得到的因子矩阵为张量的低秩近似
相对于矩阵的SVD来说，高阶张量的秩分解唯一性不需要正交性条件保证，只需满足：

这里表示矩阵的k-秩：任意k列都线性无关的最大的k张量的低秩近似
然而在低秩近似方面，高阶张量的性质比矩阵SVD差
Kolda给出了一个例子，一个立方张量的最佳秩-1近似并不包括在其最佳秩-2近似中，这说明张量的秩-k近似无法渐进地得到
下面的例子说明，张量的“最佳”秩-k近似甚至不一定存在张量的低秩近似
退化：如果一个张量能够被一系列的低秩张量任意逼近
边缘秩（borderrank）：能够任意逼近一个张量的最少的成分个数CP分解的计算
分解成多少个秩一张量（成分）之和？
通常的做法是从1开始尝试，知道碰到一个“好”的结果为止
如果有较强的应用背景和先验信息，可以预先指定

对于给定的成分数目，怎么求解CP分解？
目前仍然没有一个完美的解决方案
从效果来看，交替最小二乘（AlternatingLeastSquare）是一类比较有效的算法CP分解的计算
以一个三阶张量为例，假定成分个数已知，目标为

作为ALS的一个子问题，固定和，求解

得

再通过归一化分别求出和CP分解的计算
ALS算法并不能保证收敛到一个极小点，甚至不一定能收敛到稳定点，它只能找到一个目标函数不再下降的点

算法的初始化可以是随机的，也可以将因子矩阵初始化为对应展开的奇异向量，如将初始化为的前个左奇异向量CP分解的应用
计量心理学
语音分析
化学计量学
独立成分分析
神经科学
数据挖掘
高维算子近似
随即偏微分方程
…………Tucker分解
Tucker分解的其他名字
Three-modefactoranalysis(3MFA/Tucker3),Tucker,1966
Three-modeprincipalcomponentanalysis(3MPCA),Kroonenber