离散事件动态系统仿真.ppt

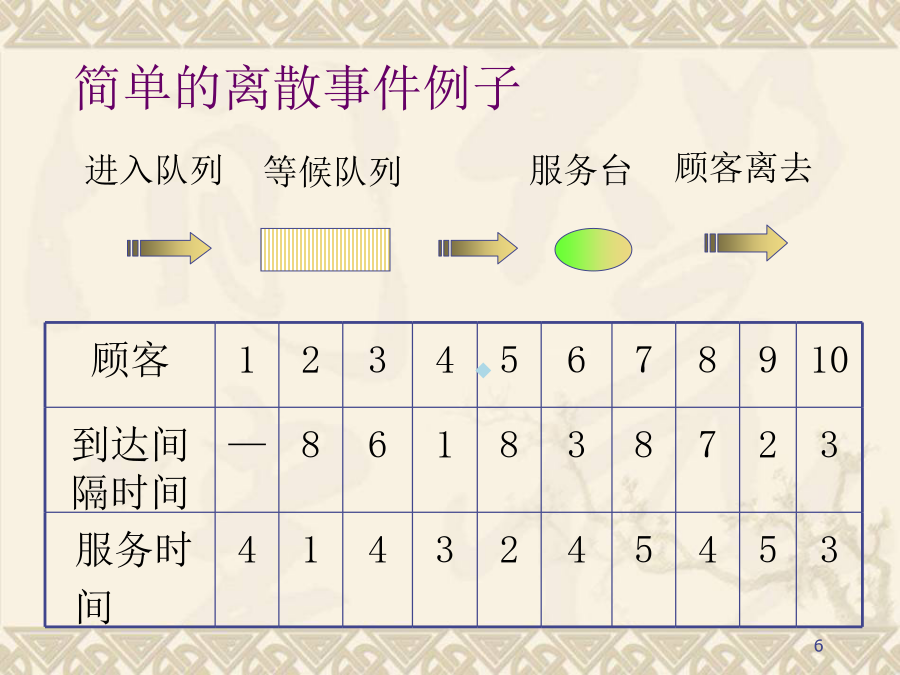
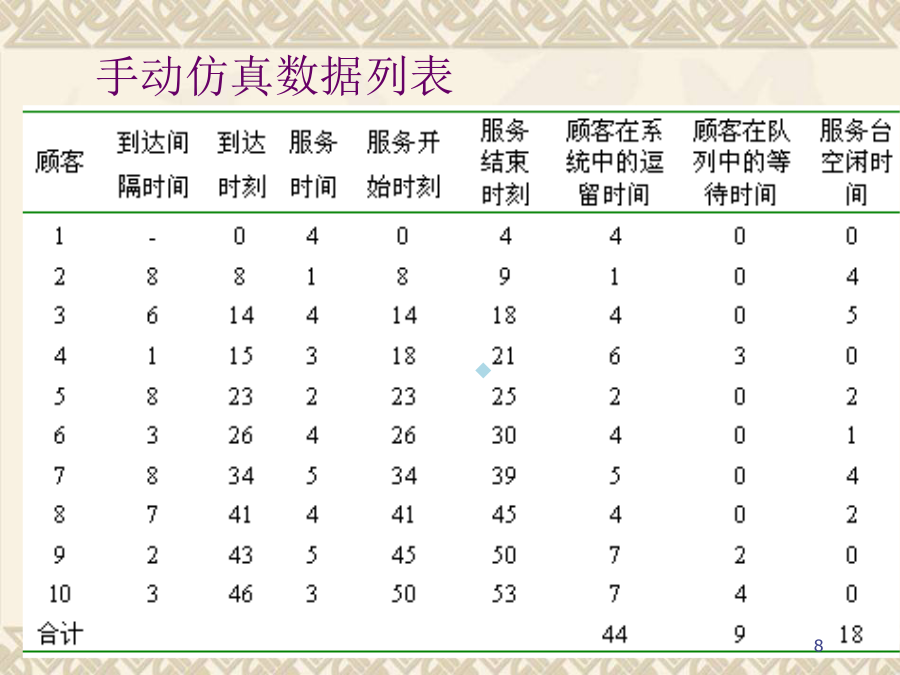
第4章离散事件动态系统仿真4.1离散事件系统与模型基本概念
4.3离散事件系统仿真策略
4.4排队系统仿真离散事件系统简介离散事件系统简介简单的离散事件例子简单的离散事件例子基本数据及手动仿真手动仿真数据列表离散事件仿真系统评价指标离散事件仿真系统评价指标离散事件动态系统所研究的主要问题离散事件动态系统所研究的主要问题4.1离散事件系统与模型离散事件动态系统DEDS（DistributedEventDynamicSystem)4.1.1描述离散事件系统的基本要素离散事件仿真的基本要素活动（Activity）：任何使系统状态发生某种变化的过程或行为。一般活动具有一定的持续时间，如顾客在银行中接受出纳员服务的过程称为服务活动；
事件（Event）：改变系统状态的某一瞬时事变称为事件。事件通常发生在活动的开始或结束时刻；
进程（Process）：实体的进程是由若干个该实体若干事件及活动构成的，它包含了这些事件和活动的逻辑关系和时序关系，例如，顾客的到达，排队、再经过出纳员服务到离去构成了一个进程。事件、活动及进程的概念4.3离散事件系统仿真模型和策略仿真程序的流程管理仿真程序的流程管理仿真程序的流程管理仿真程序的流程管理4.3离散事件系统仿真模型和策略4.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略2024/10/24.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略4.3.2离散事件系统仿真策略4.4排队系统仿真4.4排队系统仿真4.4排队系统仿真单服务台排队系统离散事件仿真模型的设计与实现2．面向事件的仿真方法
仿真时钟每次推进到系统中下一事件将要发生的时刻。因为两个事件的发生间隔通常是非固定的，并大多具有随机性，因此每次时钟推进的时间间隔是不同的。
由于面向时间间隔的仿真方法中，在每一时间间隔内发生的事件都被当作在该时间间隔的末端发生来处理，这为仿真带来了误差。该方法的另一个缺点是当两个相邻事件间的时间相差比所给定的时间间隔大很多时，仿真器可能要连续推进多个时间间隔，但并不会产生任何影响，系统的状态也不会产生任何改变，无疑这会降低仿真系统运行的效率。因此，当今离散事件仿真多采用面向事件的仿真方法。面向时间间隔的仿真方法适用于系统中状态变量很多时的场合。3．仿真模型的设计事件调度法事件调度法程序框图排队系统基本知识—先到先服务(FIFO)顾客按到达先后次序接受服务，是最通常的情形；
-—后到先服务(LIFO)后到的顾客首先接受服务，如仓库中堆积货物等；
-—随机服务(SIRO)服务台空闲时，随机地选取一名顾客进行服务；
—最短服务时间先服务(SPT)服务台空闲时，选服务时间最短的顾客。排队系统可用符号GI/G/s来表示，其中:
·GI为到达模式，用M表示马尔科夫过程，若为确定性时间间隔，用D表示;
G为服务时间分布，分布函数的符号与GI相同;
S为单队多服务台的数目，且按FIFO方式服务。
例如一个具有指数分布到达间隔时间与服务时间，且按FIFO规则服务的单服务台单队列排队系统可记为M/M/1对排队系统常用的性能指标有如下几种：应用事件调度法对排队系统进行仿真
系统的各要素如下：
·实体顾客及服务台，其中顾客是临时实体，服务台是永久实体；
·事件系统中共有两类事件，即顾客到达事件(A)和服务结束事件(D)；
·状态系统的状态为队列中的顾客数及服务台忙闲(忙=1;空闲=0)；
活动到达间隔时间与服务时间见下表。
到达事件及服务结束事件的执行过程见下页图1及图2。在事件调度法模型中FEL最多含有两个事件，下页的表在FEL中的事件写成(事件类型，事件时间，顾客号)的形式，此处加入顾客号(第I个顾客用Ci表示)是为了对顾客进行跟踪。如(D，4，C1)的含义为顾客1将在4时刻结束服务并离开系统。为了考查各顾客在系统中的逗留时间及排队时间，需知道各顾客的到达时间，这是通过(顾客号，该顾客到达时间)来记录的，如(C2，8)表示第2个顾客是在第8时刻到达的。仿真中将收集以下4个累计统计量：
顾客在系统中总的逗留时间；
顾客在系统中总的等待时间；
服务台总的空闲时间；
需等待的顾客总数。
例如一个具有指数分布到达间隔时间与服务时间，且按FIFO规则服务的单服务台单队列排队系统可记为M/M/1。
下页是上述事件调度法仿真的模拟表。随机数与随机变量的产生2．常用的随机数产生方法，线性同余法
线性同余法1951年Lehmer由提出，随机数序列中的数是由下面递推公式产生
初始值称为该随机数发生器的种子，常数称为乘子，常数称为增量，而常数m称为模数。显然，根据上式有即得到的随机数均在[0，m-1]之间。为了得到[0,1