
方差分析SPSS操作流程.pptx

骑着****猪猪









亲,该文档总共77页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

方差分析-SPSS操作流程.ppt
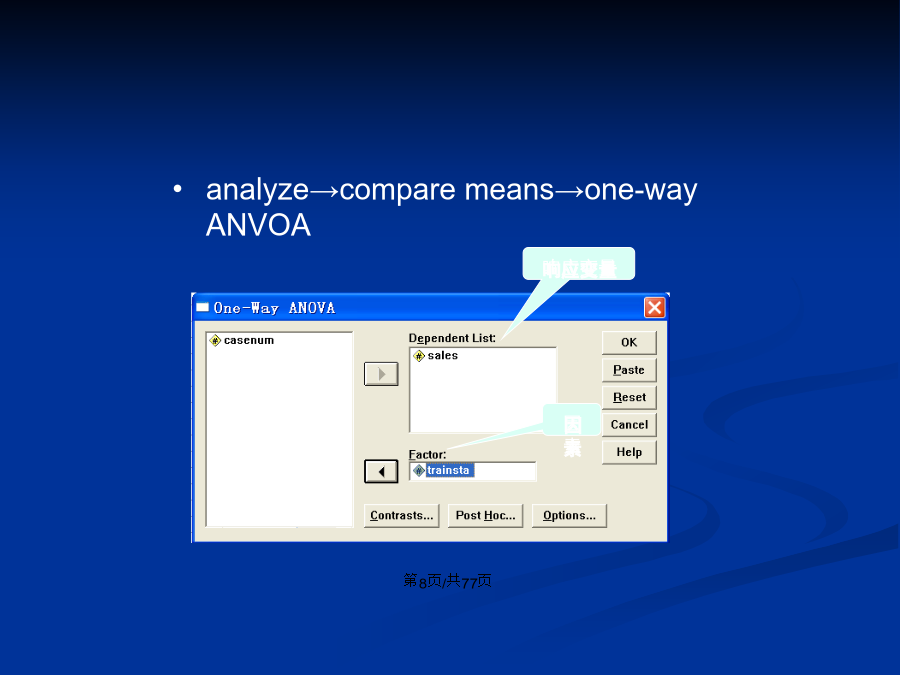
SPSS操作—方差分析方差分析由英国统计学家R.A.Fisher在1923年提出,为纪念Fisher,以F命名,故方差分析又称F检验。三种变异方差分析中的多重比较实例-多重比较方差分析的思路:将全部观测值的总变异按影响结果的诸因素分解为相应的若干部分变异,构造出反映各部分变异作用的统计量,在此基础上,构建假设检验统计量,以实现对总体参数的推断。单因素方差分析One-Way过程analyze→comparemeans→one-wayANVOAContrasts:线性组合比较。是参数或统计量的线性函数,用于检

方差分析SPSS操作流程.pptx
会计学方差分析由英国统计学家在1923年提出,为纪念Fisher,以F命名,故方差分析又称F检验。三种变异方差分析中的多重比较实例-多重比较方差分析的思路:将全部观测值的总变异按影响结果的诸因素分解为相应的若干部分变异,构造出反映各部分变异作用的统计量,在此基础上,构建假设检验统计量,以实现对总体参数的推断。单因素方差分析One-Way过程analyze→comparemeans→one-wayANVOAContrasts:线性组合比较。是参数或统计量的线性函数,用于检验均数间的关系,除了比较差异外,还包

方差分析SPSS操作流程PPT课件.ppt
SPSS操作—方差分析方差分析由英国统计学家R.A.Fisher在1923年提出,为纪念Fisher,以F命名,故方差分析又称F检验。三种变异方差分析中的多重比较实例-多重比较方差分析的思路:将全部观测值的总变异按影响结果的诸因素分解为相应的若干部分变异,构造出反映各部分变异作用的统计量,在此基础上,构建假设检验统计量,以实现对总体参数的推断。单因素方差分析One-Way过程analyze→comparemeans→one-wayANVOAContrasts:线性组合比较。是参数或统计量的线性函数,用于检

方差分析-SPSS操作流程PPT课件.pptx
SPSS操作—方差分析方差分析由英国统计学家R.A.Fisher在1923年提出,为纪念Fisher,以F命名,故方差分析又称F检验。三种变异方差分析中的多重比较实例-多重比较方差分析的思路:将全部观测值的总变异按影响结果的诸因素分解为相应的若干部分变异,构造出反映各部分变异作用的统计量,在此基础上,构建假设检验统计量,以实现对总体参数的推断。单因素方差分析One-Way过程analyze→comparemeans→one-wayANVOAContrasts:线性组合比较。是参数或统计量的线性函数,用于检

方差分析的SPSS操作-方差分析.doc
方差分析的SPSS操作-方差分析11.数据采用本章第二节所用的例1中的数据,在数据中定义一个group变量来表示五个不同的组,变量math表示学生的数学成绩。数据输入格式如图6-3(为了节省空间,只显示部分数据的输入):图6-3单因素方差分析数据输入将上述数据文件保存为“6-6-1.sav”。2.理论分析要比较不同组学生成绩平均值之间是否存在显著性差异,从上面数据来看,总共分了5个组,也就是说要解决比较多个组(两组以上)的平均数是否有显著的问题。从要分析的数据来看,不同组学生成绩之间可看作相互独立,学生的
