
钢筋溷凝土受弯构正截面承载力计算PPT课件.ppt

13****95








亲,该文档总共93页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

钢筋溷凝土受弯构正截面承载力计算PPT课件.ppt
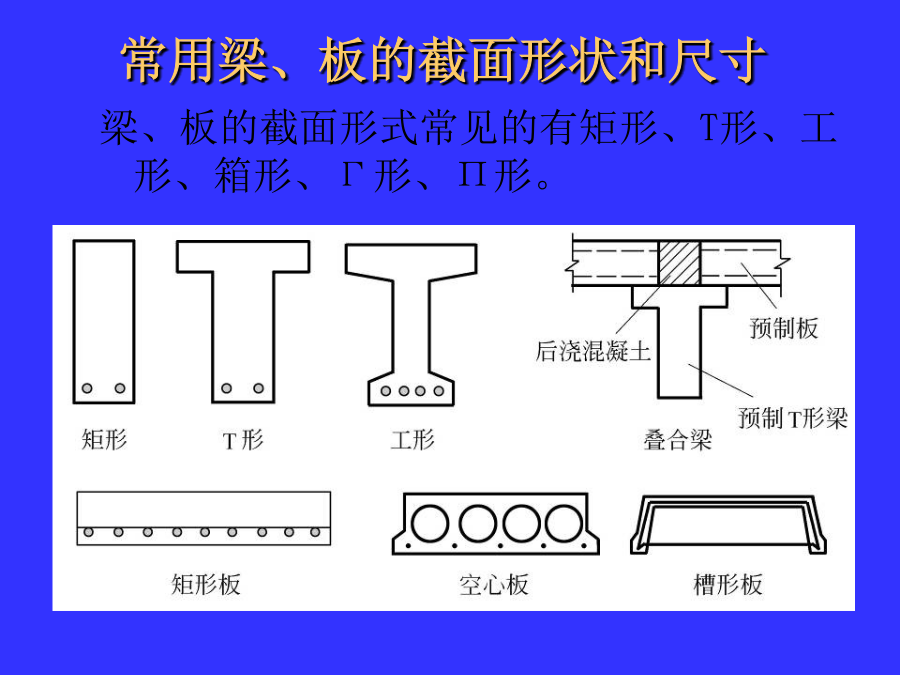
第4章钢筋混凝土受弯构件正截面承载力计算本章主要内容4.1概述4.混凝土保护层厚度:纵向受力钢筋的外表面到截面边缘的垂直距离。用c表示。为保证钢筋混凝土结构的耐久性、防火性以及钢筋与混凝土的粘结性能,钢筋的混凝土保护层厚度一般不小于25mm;5、配筋率用下述公式表示公式中各符号含义:As为受拉钢筋截面面积;b为梁宽;h0为梁的有效高度,h0=h-as;as为所有受拉钢筋重心到梁底面的距离,单排钢筋as=35mm,双排钢筋as=55~60mm。梁、板的截面形式常见的有矩形、T形、工形、箱形、Γ形、Π形。预应

钢筋溷凝土受弯构件修课件学习.pptx
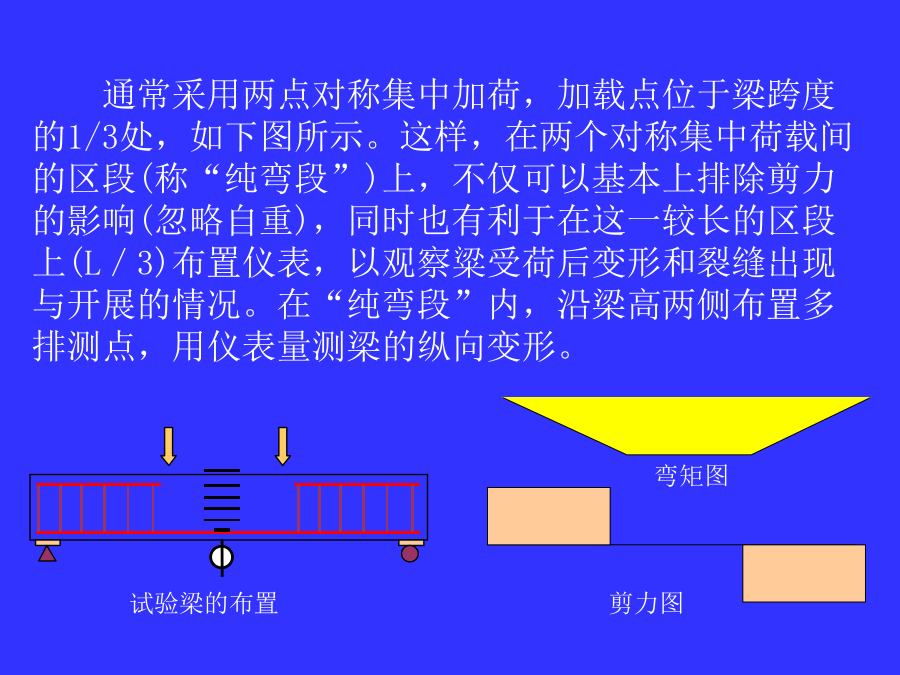
会计学第一节钢筋混凝土受弯构件的一般构造规定第二节受弯构件正截面性能的试验研究第三节受弯构件正截面承载力计算第四节受弯构件正截面受弯承载力的设计第五节受弯构件剪弯段的受力特点及斜截面受剪承载力第六节受弯构件斜截面的受剪承载力计算第七节受弯构件斜截面受弯承载力及有关构造要求第一节钢筋混凝土受弯构件的一般构造规定第二节受弯构件正截面性能的试验研究/二、梁的正截面破坏特征(一)配筋率:=As/(bh0)(二)适筋破坏:受拉钢筋先屈服,受压区混凝土后压碎;破坏前有预兆,属延性破坏。(三)少筋破坏:受拉区混凝土一

钢筋溷凝土受弯构件学习.pptx
会计学梁板结构第二节钢筋混凝土受弯构件

混凝土受弯构-斜截面承载力计算ppt课件.ppt
课堂小结第五章受弯构件斜截面承载力计算研究构件在剪力作用下斜截面的受力特点、破坏形式及其影响因素,并据此提出了受弯构件斜截面承载力的计算公式及其适用条件。给出了一些常用的防止斜截面破坏的构造措施。无腹筋梁斜截面破坏的形式;影响斜截面承载力的主要因素。纵向钢筋的弯起与截断。§5-1概述一、基本概念1、斜截面破坏:在受弯构件的剪压区,由于剪力和弯矩的共同作用,在主拉应力和主压应力的共同作用下,构件截面处于拉压复合受力状态,产生斜向裂缝而破坏。斜截面破坏具有脆性性质,工程中不允许出现。2、腹筋:为了抵抗些裂缝的

第3章-钢筋溷凝土轴心受力构件正截面承载力计算.ppt
●我们所要学习的内力(荷载效应)有四种:弯矩(M)、剪力(V)、轴力(N)和扭矩(T)。●基本受力构件是按照荷载在构件上所产生的内力来分类的,就我们以下所学习的内容看,有受弯构件、受压构件、受拉构件和受扭构件,但单一受力的构件几乎不存在,所以我们的思路是从单一到组合、由简单到复杂。●在学习基本构件时,可遵循一定的规律:①了解工程实际中的结构形式;②根据试验过程的描述,认清构件在极限破坏时的表现形态及受力状态;③理解对应的计算模型,并能据此熟悉计算简图(应力分布图);④根据计算简图可推导出基本计算公式;⑤能
