三向地震波的合理选取和人工定义.pptx

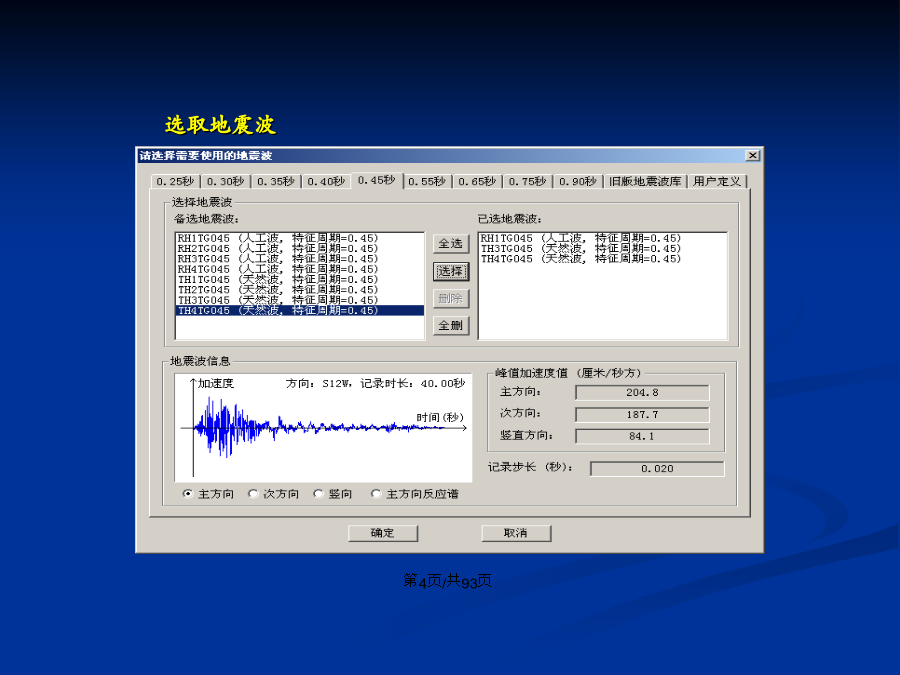
会计学18.1。时程分析与地震波新抗震规范5.1.2条规定，“特别不规则的建筑、甲类建筑和表5.1.2-1所列高度范围的高层建筑，应采用时程分析法进行多遇地震下的补充计算”，“采用时程分析法时，应按建筑场地类别和设计地震分组选用不少于两组的实际强震记录和一组人工模拟的加速度时程曲线”。
地震波与反应谱应在“统计意义上相符”。
时程分析法单波和平均值的底部剪力应不小于按反应谱方法得到的底部剪力的“65％”和“80％”等限值。
新抗震规范5.5.3条规定，除可以采用简化方法计算外的建筑结构，可采用静力弹塑性分析方法或弹塑性时程分析方法。18.2。三向地震波的合理选取选取地震波实测地震波——特征参数实测地震波——反应谱实测地震波——东南向40度作用实测地震波——西南向50度作用实测地震波——竖向作用保留的旧版地震波库18.3。如何人工定义地震波人工输入地震波选择19.1。弹塑性分析目的、意义
19.2。弹塑性分析的规范规定
19.3。简化弹塑性分析方法及适用范围
19.4。静力弹塑性分析方法
19.5。动力弹塑性分析方法19.1。弹塑性分析目的、意义19.2。弹塑性分析的规范规定《建筑抗震设计规范》《高层混凝土结构技术规程》《高层民用建筑钢结构技术规程》19.3。简化弹塑性分析方法及应用范围19.4。静力弹塑性分析方法抗倒塌分析图静力弹塑性分析方法的特点19.5。动力弹塑性分析方法动力弹塑性分析方法的特点20.1。弹塑性分析软件整体功能简介
20.2。弹塑性静力分析软件PUSH简介
20.3。弹塑性静力分析软件PUSH工程实例
20.4。弹塑性静力分析软件PUSH验证20.1。弹塑性分析软件整体功能简介/20.2。弹塑性静力分析软件PUSH简介PUSH软件主要参数说明材料参数调整：通过该系列参数的调整，可以按照用户实际情况调整混凝土和钢的单轴本构关系曲线形状，考虑混凝土破坏、受到约束等情况。
铰的相对刚度界限：为杆件塑性铰的判断条件，例如填入0.8的含义是杆端截面的刚度与初始刚度相比退化了80％时认为出现了塑性铰。
墙高斯点破坏条件：剪力墙通过用户给出破坏应变界限来判断破坏情况。
杆元细分、墙元细分：用户可以人为的细分杆件单元。
楼板考虑为梁翼缘的相对宽度：通过该参数，用户可以考虑楼板对于梁的刚度贡献。/////20.3。弹塑性静力分析软件PUSH工程实例——高层混凝土结构高层钢结构20.4。弹塑性静力分析软件PUSH工程实例21.1。弹塑性动力分析软件EPDA简介
21.2。弹塑性动力分析软件EPDA工程实例
21.3。弹塑性动力分析软件EPDA验证
21.1。弹塑性动力分析软件EPDA简介EPDA软件主要参数说明ε(压)“塑性铰判断方法”：给出了“弹性积分点比例”和“截面刚度退化比例”两种判断杆系构件的塑性铰的方法。“弹性积分点比例”方法是按照构件截面的积分点仍然保持弹性的比例来判断构件的端部是否出现塑性铰。“截面刚度退化比例”是按照结构进入弹塑性状态后的杆端截面刚度与初始截面刚度的比值来判断构件是否形成塑性铰。

“塑性铰判断参数”：该参数与“塑性铰判断方法”相对应，填入0.0～1.0之间的一个数值。当通过“弹性积分点比例”判断塑性铰时，如果填入“0.3”表示“只有30％的端截面积分点保持弹性时出现塑性铰”。当选择当通过“截面刚度退化比例”判断塑性铰时，如果填入“0.3”表示“截面刚度退化为初始截面刚度的30％时出现塑性铰”。“动力微分方程组解法”：目前程序提供给用户两种求解动力微分方程组的方法，Wilson-θ法和Newmark-β法。这两种方法的计算结果差别不大，用户根据需要选择。
“非线性方程组解法”：程序提供了两种求解非线性方程组的迭代方法，Newton-Raphson迭代和modifiedNewton-Raphson迭代。这两种方法的迭代次数和适用条件是不同的。对于混凝土结构一般建议采用Newton-Raphson迭代进行计算。
“非线性迭代步数限值”：该限值规定了非线性迭代的最多次数，当达到该步数限值时，如果还没有收敛，需要缩短步长进行计算。该值不宜取的过大，“10”左右比较合适，否则会明显增加计算时间。
“非线性迭代收敛精度”：EPDA程序衡量非线性迭代是否收敛的依据是“不平衡力向量范数”，一般认为0.01～0.001左右的精度是可以满足工程要求的。该值不宜取的过小，否则程序将难以收敛。“最佳收敛次数”：EPDA程序中提供了计算步长自动伸缩求解策略。所谓“最佳收敛次数”是指用户认为多少次迭代收敛是比较合理的。当程序的迭代次数小于该值时，表示计算步长过小，程序会自动增加计算步长；当程序的迭代次数大于该值时，表示计算步长过大，程序会自动缩减计算步长。通常认为一个计算时间步内，结构应该在3～5次迭代后收敛。
“不收敛时