弹塑性力学弹塑性本构关系.pptx

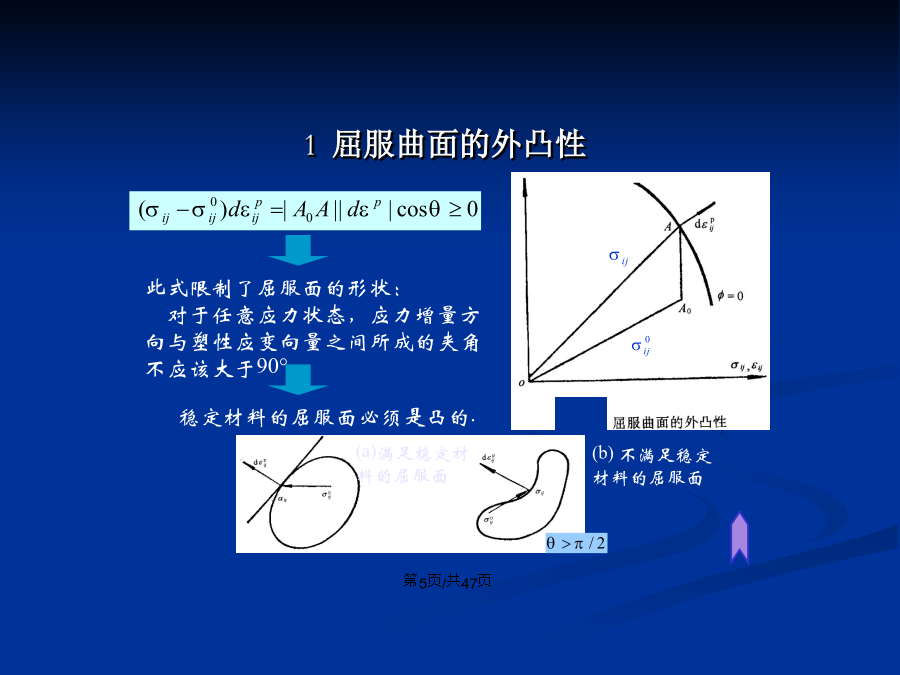
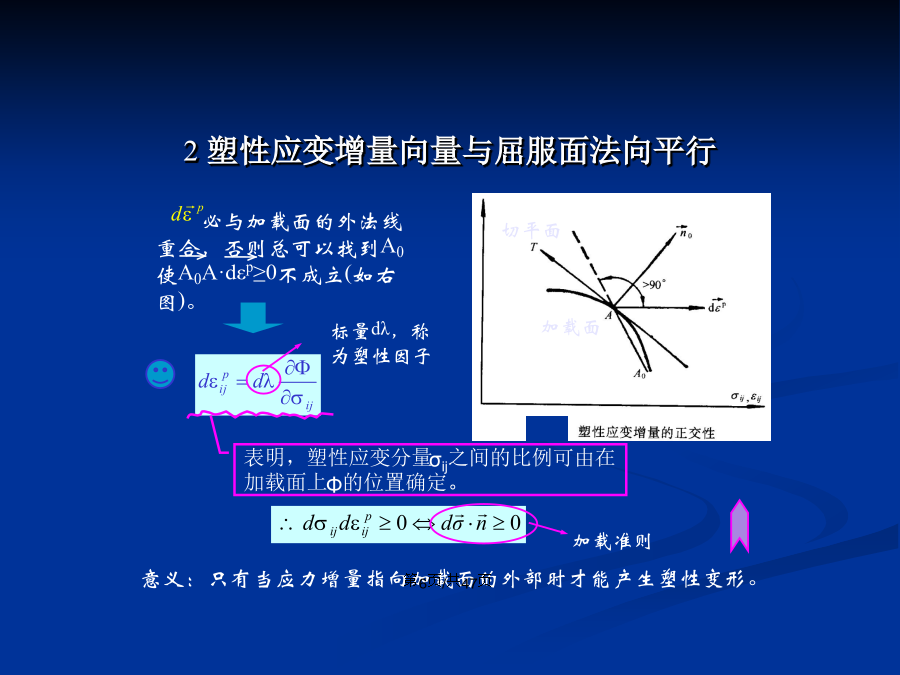
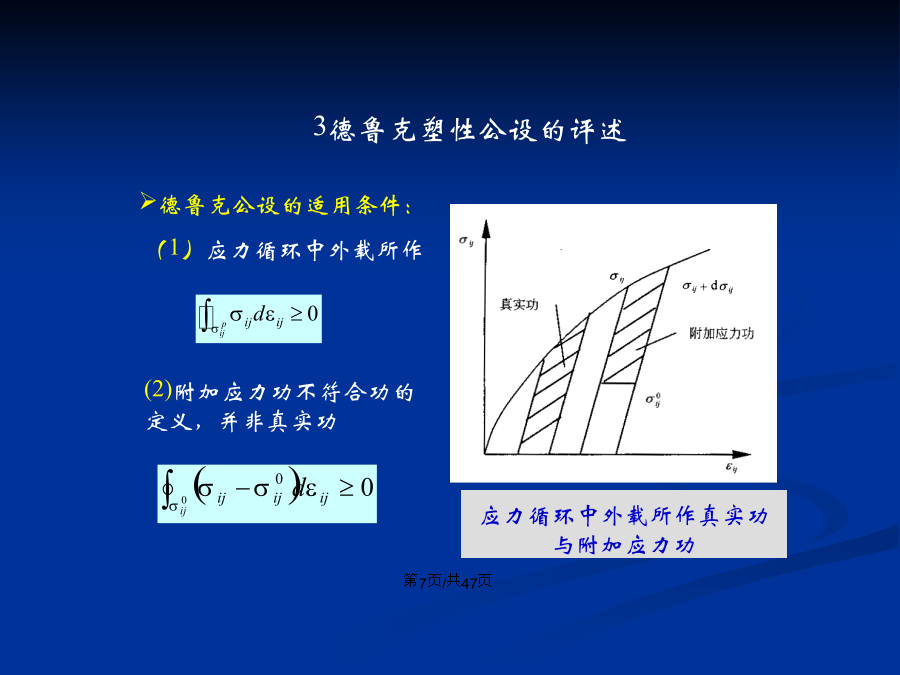
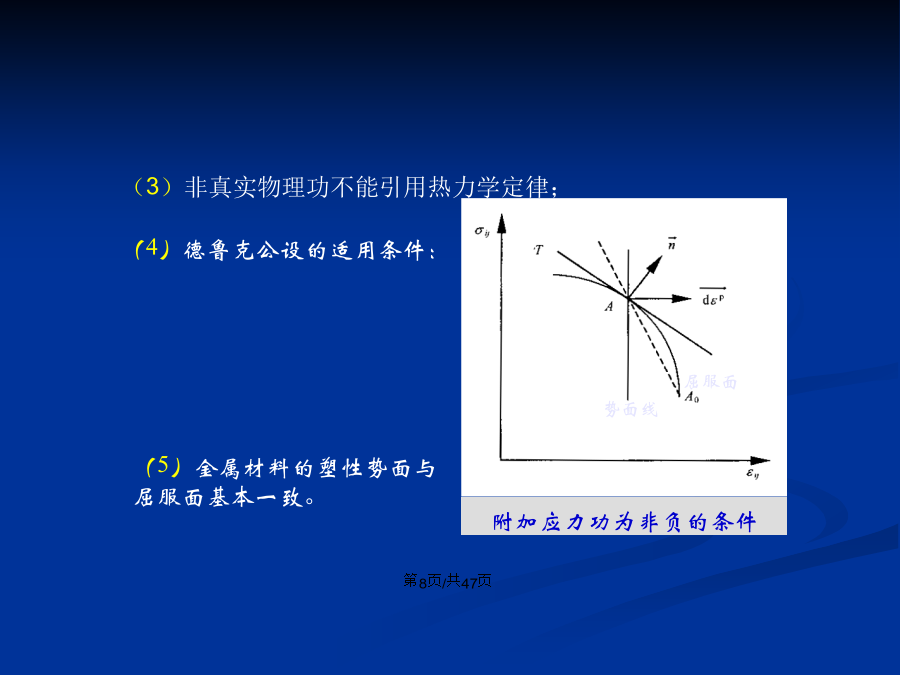
会计学附加应力对附加应变负做功，即(2)德鲁克塑性公设的表述在应力循环中，外载所作的功为：(3)德鲁克塑性公设的重要推论1屈服曲面的外凸性2塑性应变增量向量与屈服面法向平行3德鲁克塑性公设的评述（4）德鲁克公设的适用条件：
①ij0在塑性势面与屈服面之内时，德鲁克公设成立；
②ij0在塑性势面与屈服面之间时，德鲁克公设不成立；依留申塑性公设的表述残余应力增量与塑性应变增量存在关系：由图(a)可知，对于弹性性质不随加载面改变的非耦合情况，外部作用在应变循环内做功WI和应力循环所作的外部功之间仅差一个正的附加项：塑性位势理论与流动法则上式就称为塑性位势理论。它表明一点的塑性应变增量与通过该点的塑性势面存在着正交关系，这就确定了应变增量的方向，也就确定了塑性应变增量各分量的比值。与德鲁克公设表达式比较，可以看出，服从于德鲁克公设的材料，塑性势函数g就是屈服函数Φ。即g=Φ，由此得到的塑性应力应变关系通常称为与加载条件相关联的流动法则。如果g≠Φ，即屈服面与塑性应变增量不正交，则其相应的塑性应力应变关系称为非关联流动法则。3.2硬化规律硬化规律：加载面在应力空间中的位置、大小和形状的变化规律。（确定加载面依据哪些具体的硬化参量而产生硬化的规律称为硬化定律）
硬化模型：实际土体硬化规律+简化假设（如采用等值面硬化理论，主应力方向不旋转，加载面形状不变等）
等向强化模型在应力空间中，这种后继屈服面的大小只与最大的应力状态有关，而与中间的加载路径无关。在右图中，路径1与路径2的最终应力状态都刚好对应于加载过程中最大应力状态，因此两者的最终后继屈服是一样的；而路径3的最终后继屈服面由加载路径中最大应力状态来定。随动强化模型包辛格逆效应（Bauschinger）分直接包辛格效应及包辛格逆效应。直接包辛格效应指拉伸后钢材纵向压缩屈服强度小于纵向拉伸屈服强度，如图1所示；包辛格逆效应在相反的方向产生相反的结果，如图2所示。混合强化模型加工硬化规律塑性功Wp硬化定律：塑性应变εijp硬化定律：塑性体应变εvp硬化定律3.3弹塑性本构关系塑性增量理论又称为塑性流动理论，它把塑性变形看成非线性流动。塑性增量理论把应变增量分为弹性应变增量和塑性应变增量两部分，即式中，弹性应变增量应用广义虎克定律计算，塑性应变增量根据塑性增量理论计算。塑性增量理论主包括三个部分：关于屈服面理论，关于流动规则理论，关于加工硬化(或软化)理论。应用弹塑性增量理论计算塑性应变：首先，要确定材料的屈服条件，对加工硬化材料，需要确定材料是否服从相关联流动规则。若材料服从不相联流动规则，沿需确定材料的塑性势函数。然后，还需要确定材料的硬化或软化规律。最后可运用流动规则理论确定塑性应变增量的方向，根据硬化规律计算塑性应变增量的大小。一个普遍的弹塑性模量张量表达式将(b)代入(a)得：弹性状态广义虎克定律增量表达式于是：弹性常数关系表无静水压力影响的理想弹塑性材料本构关系屈服函数记为：根据理想弹塑性材料的本构方程可表示为于是：(2)Druker-Prager模型塑性体积应变：