
14元阵列天线方向图及其MATLAB仿真.pdf

17****21


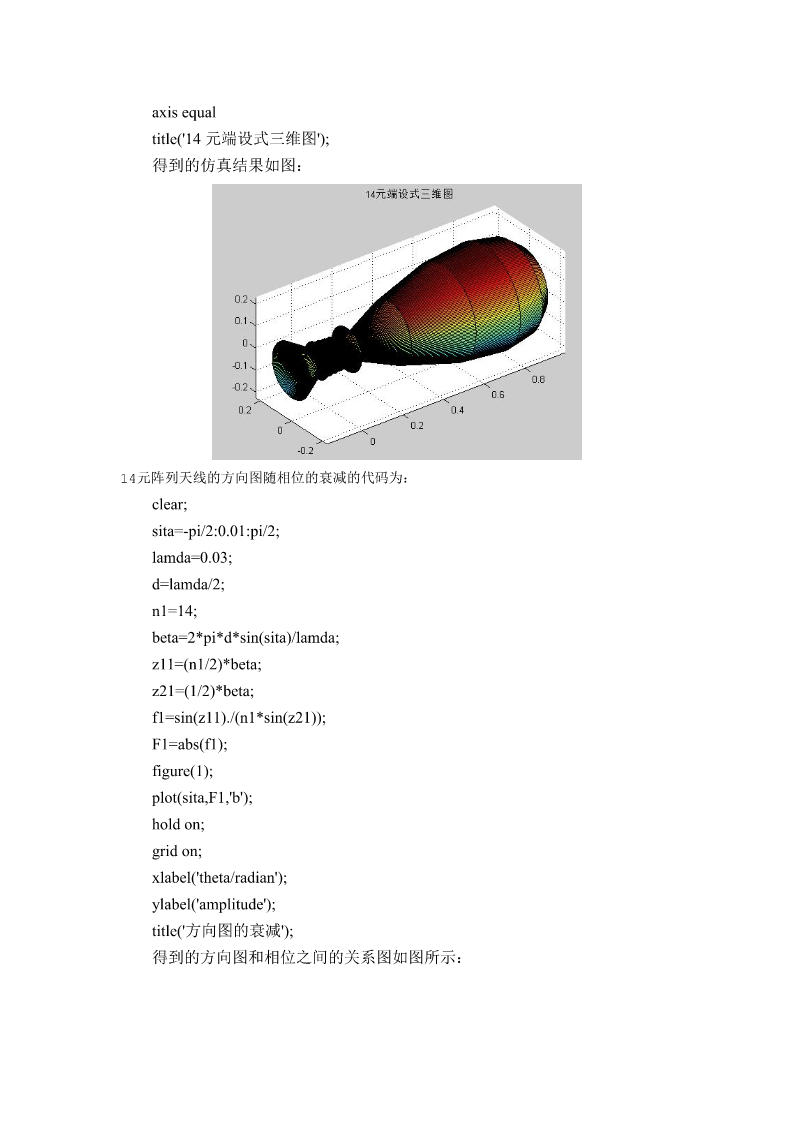

在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

14元阵列天线方向图及其MATLAB仿真.doc
5/5阵列天线方向图与其MATLAB仿真1设计目的1.了解阵列天线的波束形成原理写出方向图函数2.运用MATLAB仿真阵列天线的方向图曲线3.变换各参量观察曲线变化并分析参量间的关系2设计原理阵列天线:阵列天线是一类由不少于两个天线单元规那么或随机排列并通过适当激励获得预定辐射特性的特殊天线。阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整,这就使阵列天线具有各种不同的功能,这些功能是单个天线无法实现的。在本次设计中,讨论的是均匀直线阵天线。

14元阵列天线方向图及其MATLAB仿真.pdf
阵列天线方向图及其MATLAB仿真1设计目的1.了解阵列天线的波束形成原理写出方向图函数2.运用MATLAB仿真阵列天线的方向图曲线3.变换各参量观察曲线变化并分析参量间的关系2设计原理阵列天线:阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整,这就使阵列天线具有各种不同的功能,这些功能是单个天线无法实现的。在本次设计中,讨论的是均匀直线阵天线。均匀直线

阵列天线、阵列天线方向图的赋形装置及赋形方法.pdf
本发明公开了一种阵列天线、阵列天线方向图的赋形装置及赋形方法,克服现有技术中阵列天线赋形时拟合度低及天线波束覆盖范围有限的问题。该方法包括:获取阵列天线各个阵元在耦合条件下的方向图;根据各个阵元在所述耦合条件下的方向图,随机生成初始种群;为所述初始种群中的每个个体计算适应度值,并根据所述适应度值选择赌轮盘策略或者精英选择策略;根据所述选择器所选择的赌轮盘策略或者精英选择策略,配合适应度选择再生个体,并对所述再生个体进行优化,生成新的个体;符合预设结束规则时输出所述阵列天线的最优方向图。本发明的X波段天线阵

带有MPPT 功能的光伏阵列 Matlab 通用仿真模型.pdf
系统仿真学报Vol.17No.5•1248•JOURNALOFSYSTEMSIMULATIONMay2005带有MPPT功能的光伏阵列Matlab通用仿真模型茆美琴,余世杰,苏建徽(1合肥工业大学能源研究所,合肥230009;2教育部光伏系统工程研究中心,合肥230009)摘要:基于光伏模块直流物理模型,在matlab仿真环境下,开发了光伏阵列通用仿真模型。利用该模型,可以模拟任意太阳辐射强度、环境温度、光伏模块参数、光伏阵列串并联方式组合下的光伏阵列I-V特性。此外,该模型还融合了光伏阵列的最大功率跟踪
带有MPPT功能的光伏阵列Matlab通用仿真模型.pdf
