
土压力及挡土结构.pptx

骑着****猪猪





亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

土压力及挡土结构.pptx
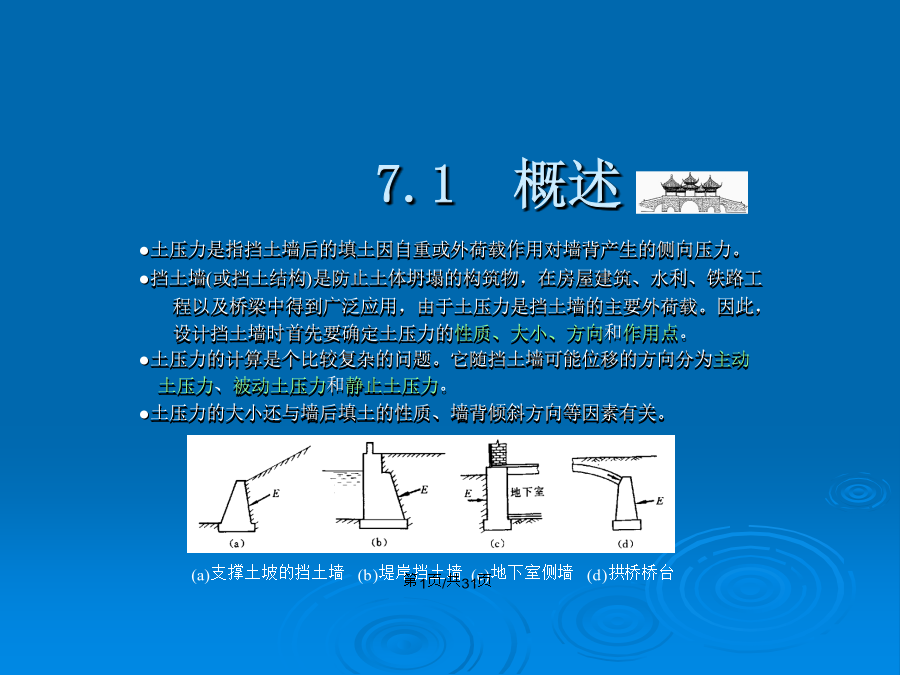
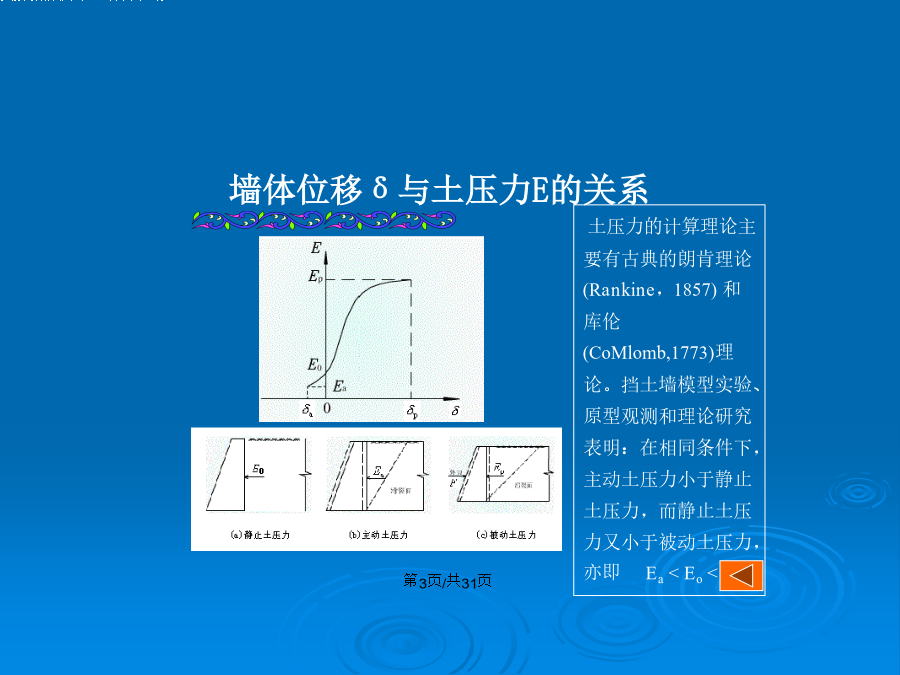
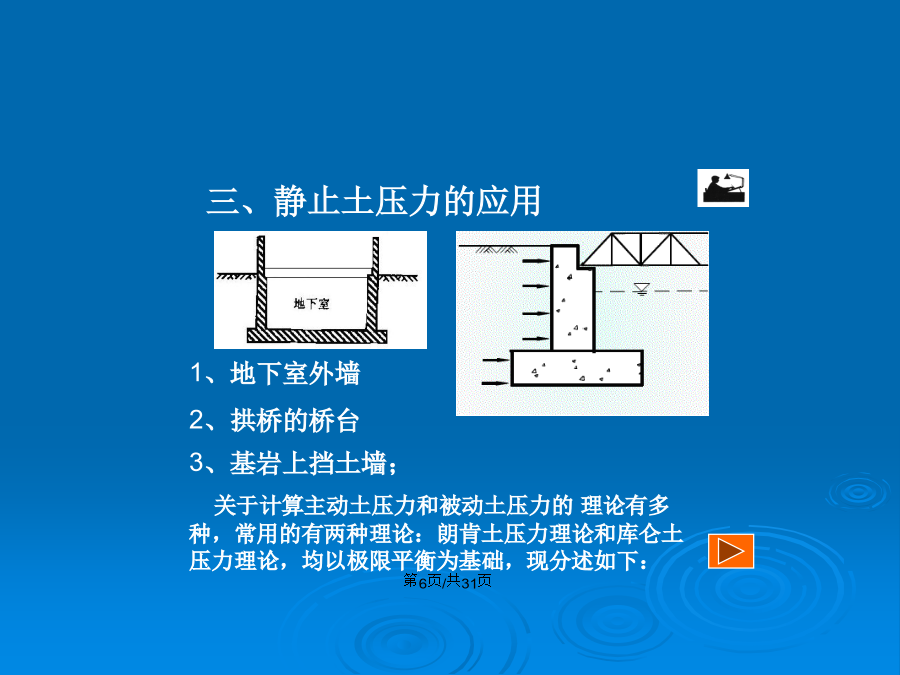
土压力及挡土结构7.1概述挡土墙上的土压力挡土墙土压力的大小及其分布规律受到墙体可能的移动方向、墙后填土的种类、填土面的形式、墙的截面刚度和地基的变形等一系列因素的影响。根据墙的位移情况和墙后土体所处的应力状态,土压力可分为以下三种:(1)静止土压力:当挡土墙静止不动,土体处于弹性平衡状态时,土对墙的压力称为静止土压力,一般用E0表示。(2)主动土压力:当挡土墙向离开土体方向偏移至土体达到极限平衡状态时,作用在墙上的土压力称为主动土压力,一般用Ea表示。(3)被动土压力:当挡土墙向土体方向偏移至土体达到极

挡土结构与土压力.doc
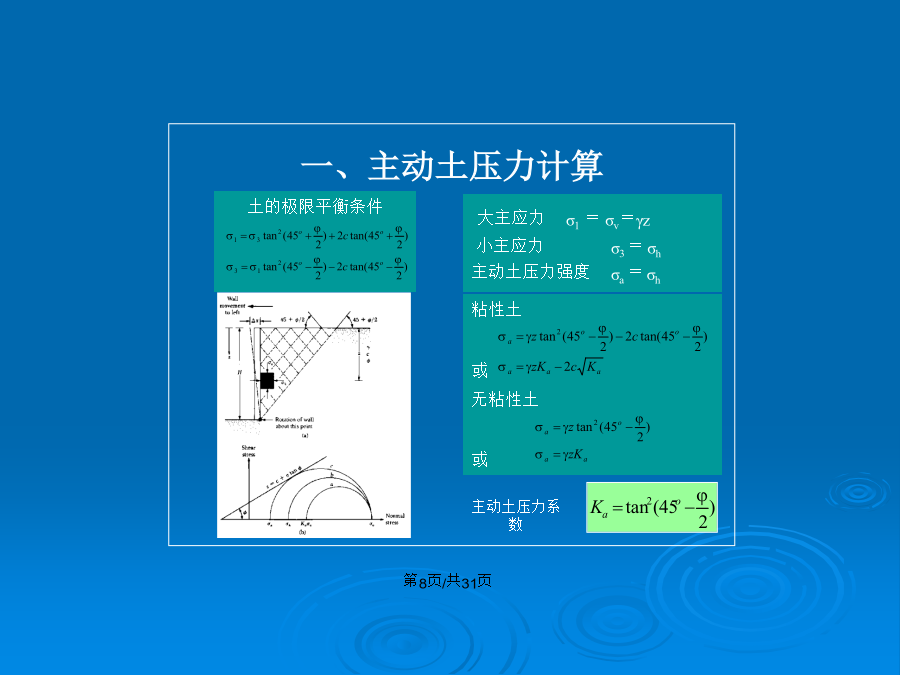
任务1挡土结构与土压力一、填空题(每空2分,共10分)1、土压力可分为、和,在相同的条件下,三种土压力的关系为。静止土压力、被动土压力、主动土压力2、朗肯土压力理论的假定是、、。墙刚性墙背垂直、墙背光滑3、库仑土压力理论的假定是、、。墙后填土是均匀的散粒土、滑动破坏面为通过墙踵的平面、滑动携体4、某挡土墙墙背垂直、光滑,填土面水平,填土为中砂,若墙高为2m时作用于墙背上的主动土压力为20kN/m,则墙高为4m时作用于墙背上的主动土压力为kN/m。405、重力式挡土墙按墙背倾角不同可分为、和三种。仰斜式、俯

挡土结构与土压力.docx
任务1挡土结构与土压力一、填空题(每空2分,共10分)1、土压力可分为、和,在相同的条件下,三种土压力的关系为。静止土压力、被动土压力、主动土压力2、朗肯土压力理论的假定是、、。墙刚性墙背垂直、墙背光滑3、库仑土压力理论的假定是、、。墙后填土是均匀的散粒土、滑动破坏面为通过墙踵的平面、滑动携体4、某挡土墙墙背垂直、光滑,填土面水平,填土为中砂,若墙高为2m时作用于墙背上的主动土压力为20kN/m,则墙高为4m时作用于墙背上的主动土压力为kN/m。405、重力式挡土墙按墙背倾角不同可分为、和三种。仰斜式、俯

挡土结构物的土压力.ppt
第七章挡土结构物的土压力§7.1土压力概述一、土压力类型2.主动土压力4.三种土压力之间的关系二、静止土压力计算§7.2朗肯土压力理论pa二、主动土压力h/32c√Ka三、被动土压力讨论:当c>0,粘性土四、例题分析【解答】五、几种常见情况下土压力计算2.成层填土情况(以无粘性土为例)3.墙后填土存在地下水(以无粘性土为例)六、例题分析【解答】§7.3库仑土压力理论土楔在三力作用下,静力平衡主动土压力与墙高的平方成正比三、例题分析§7.4土压力计算方法讨论挡土墙产生离开填土方向位移,墙后填土达到极限平衡状

挡土结构物的土压力.ppt
第七章挡土结构物的土压力§7.1土压力概述一、土压力类型2.主动土压力4.三种土压力之间的关系二、静止土压力计算§7.2朗肯土压力理论pa二、主动土压力h/32c√Ka三、被动土压力讨论:当c>0,粘性土四、例题分析【解答】五、几种常见情况下土压力计算2.成层填土情况(以无粘性土为例)3.墙后填土存在地下水(以无粘性土为例)六、例题分析【解答】§7.3库仑土压力理论土楔在三力作用下,静力平衡主动土压力与墙高的平方成正比三、例题分析§7.4土压力计算方法讨论挡土墙产生离开填土方向位移,墙后填土达到极限平衡状
