应力应变分析强理论学习资料.pptx

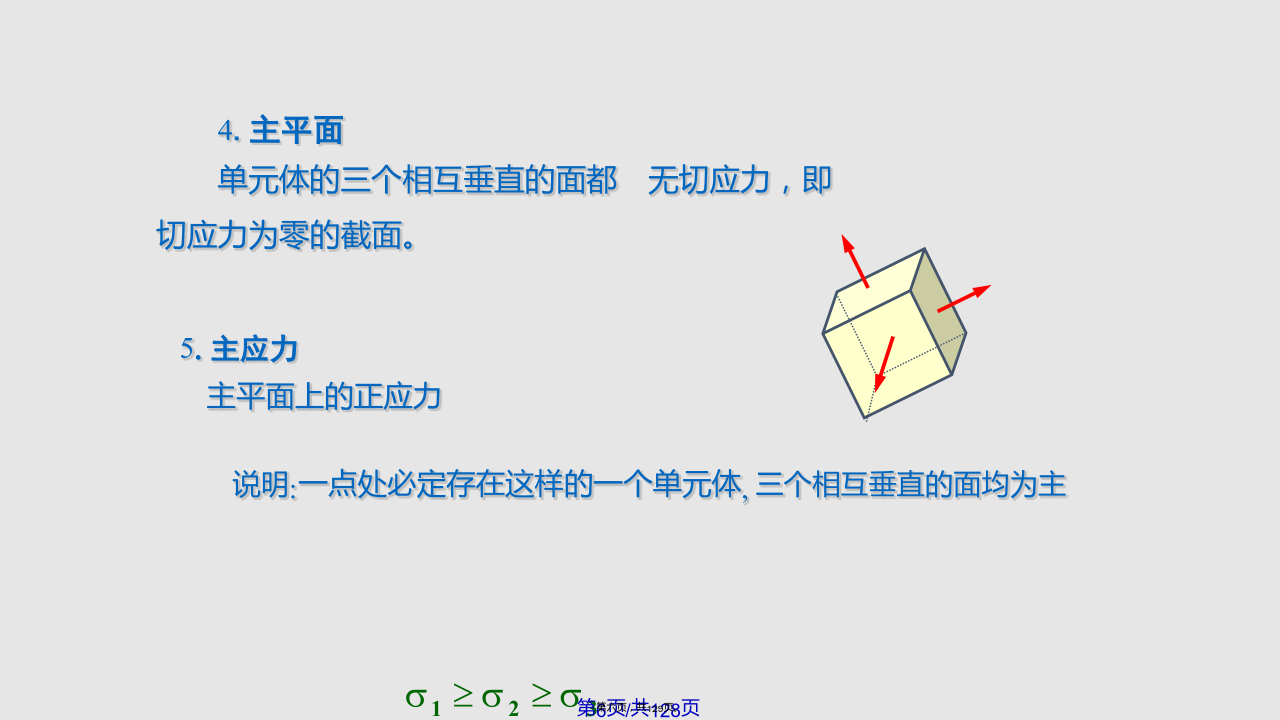
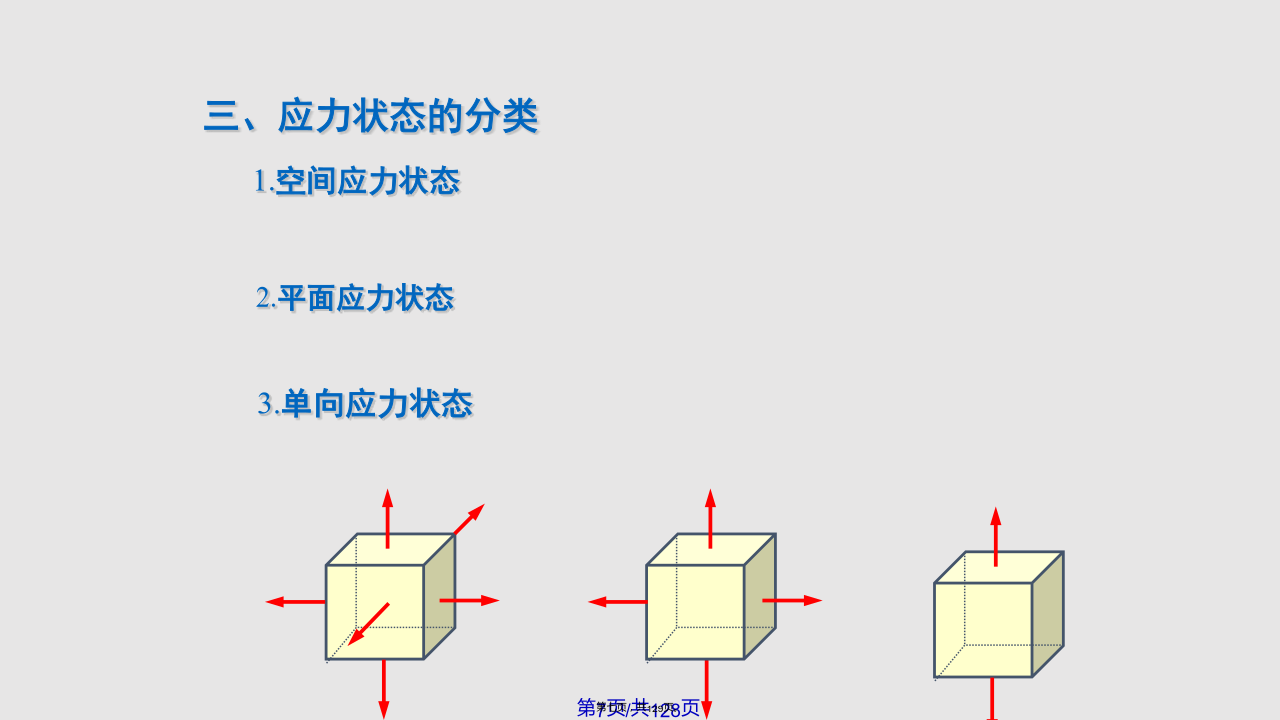
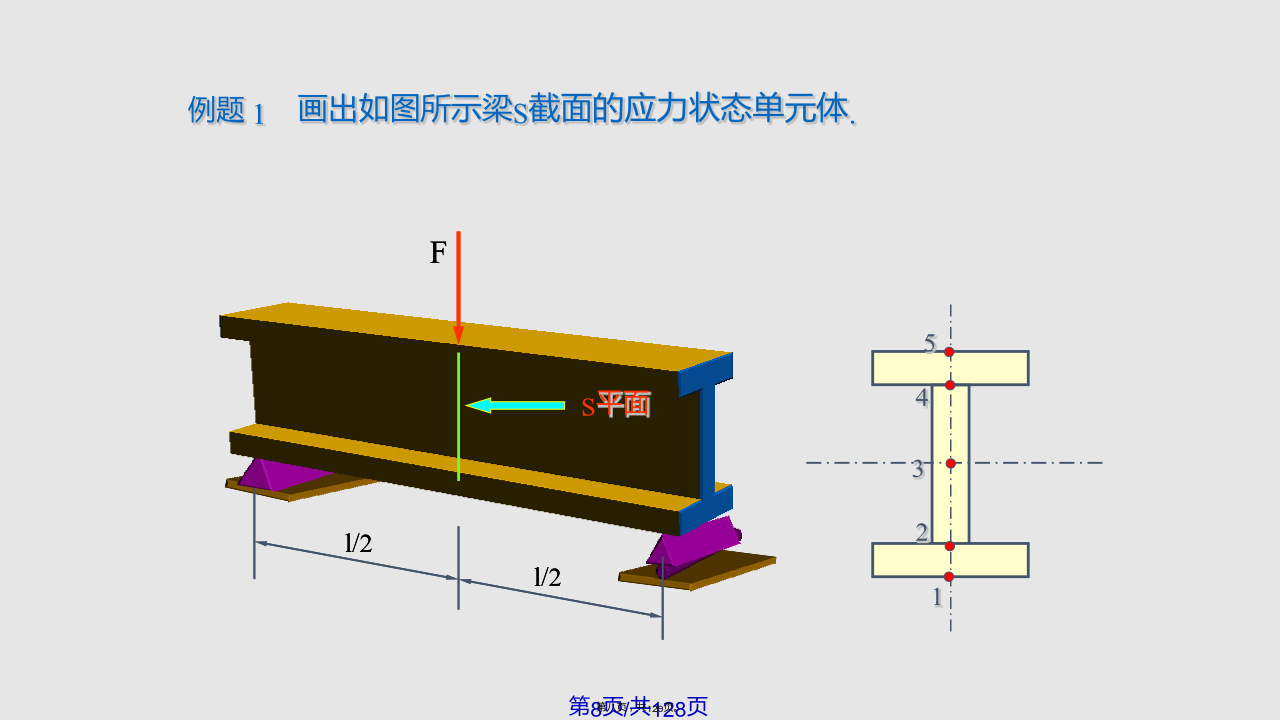
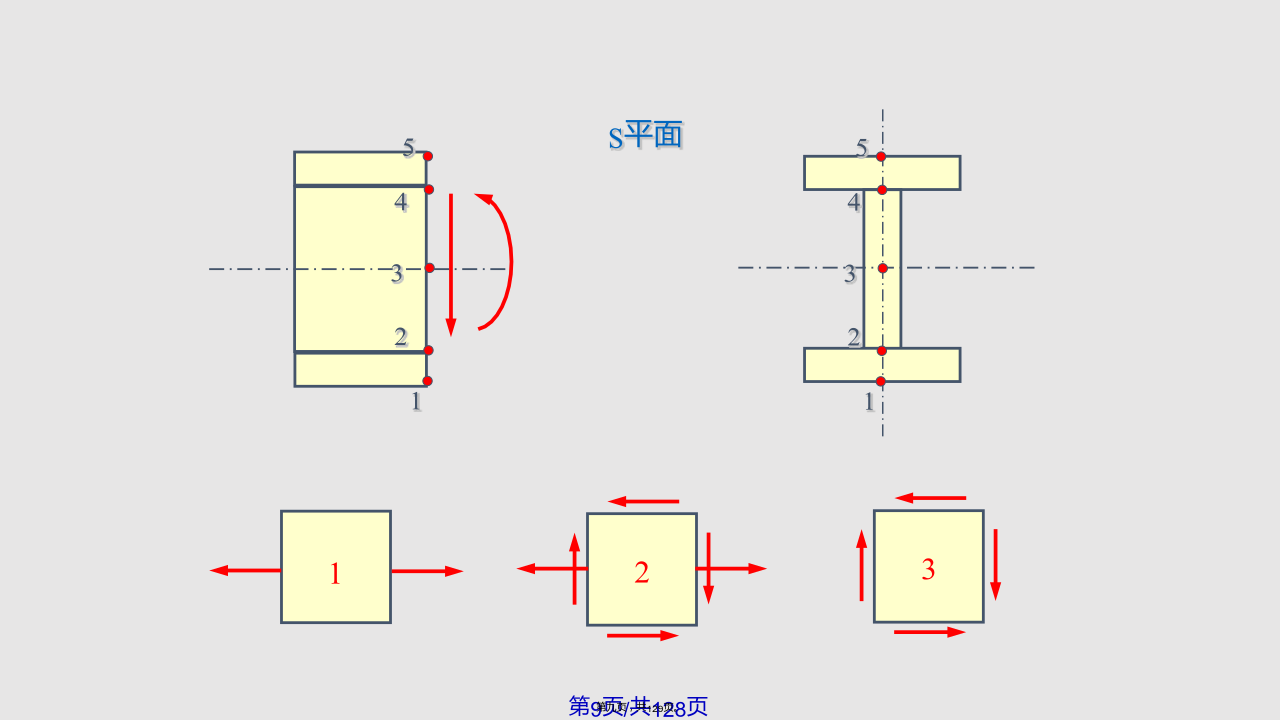
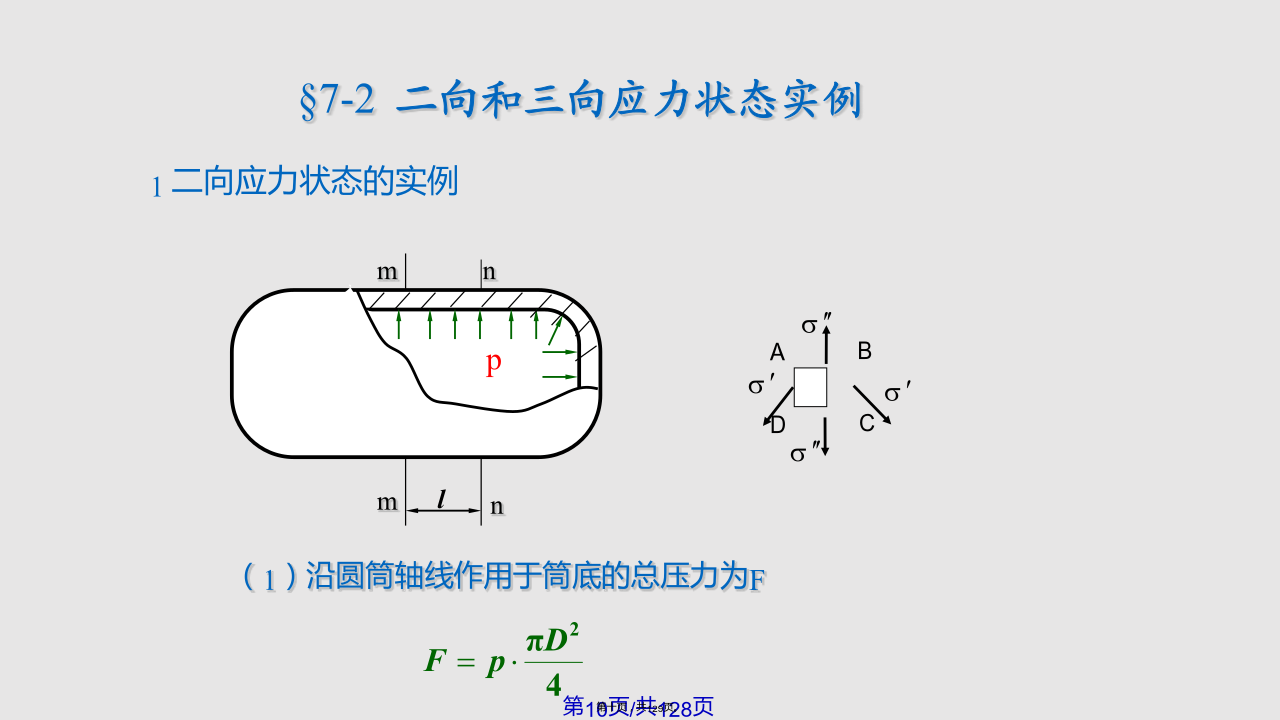
§7-1应力状态概述低碳钢?（1）拉中有剪,剪中有拉;
（2）不仅横截面上存在应力,斜截面上也存在应力;
（3）同一面上不同点的应力各不相同;
（4）同一点不同方向面上的应力也是各不相同二、应力状态的研究方法4.主平面
单元体的三个相互垂直的面都无切应力，即切应力为零的截面。三、应力状态的分类S平面例题2圆球形容器的壁厚为，内径为D,内压强为p。
试求容器壁内某单元体的应力。平衡方程平面应力状态的普遍形式如图所示.单元体上有x,xy和y,yx§7-3平面应力状态分析-解析法一、斜截面上的应力设斜截面的面积为dA,a-e的面积为dAcos,a-f的面积为dAsin化简以上两个平衡方程最后得二、最大正应力及方位2.最大正应力（1）当x>y时,0是x与max之间的夹角
二、最大切应力及方位2.最大切应力例题4简支梁如图所示.已知m-m截面上A点的弯曲正应力和切应力分别为=-70MPa,=50MPa.确定A点的主应力及主平面的方位.因为x<y，所以0=27.5°与min对应x（2）求主应力和主单元体的方位解:（1）求主平面方位§7-3平面应力状态分析-图解法（1）建-坐标系,选定比例尺D（1）该圆的圆心C点到坐标原点的距离为三、应力圆的应用
证明：（1）点面之间的对应关系:单元体某一面上的应力,必对应于应力圆上某一点的坐标.将半径CD逆时针转动2=60°到半径CE,E点的坐标就代表=30°斜截面上的应力。例题8两端简支的焊接工字钢梁及其荷载如图所示,梁的横截面尺寸示于图中.试绘出截面C上a,b两点处的应力圆,并用应力圆求出这两点处的主应力.例题9单元体的应力如图所示,作应力圆,并求出主应力和最大切应力值及其作用面方位.由x,xy定出D点§7-5平面应变状态分析将Oxy坐标绕O点旋转一个角，得到一个新Ox'y'坐标系.（1）只有正值x存在（2）只有正值y存在（3）只有正值切应变xy存在根据叠加原理,x,y和xy同时存在时,O点沿x´方向的线应变为二、主应变数值及其方位y在x,y,z同时存在时,x方向的线应变x为上式称为广义胡克定律（GeneralizedHooke’slaw）
3.主应力-主应变的关系（Principalstress-principalstrainrelation）二、各向同性材料的体积应变（Thevolumetricstrain
forisotropicmaterials）体积应变（volumetricstrain）为1.纯剪切应力状态下的体积应变（Volumetricstrainforpureshearingstress-state）这两个单元体的体积应变相同如果变形前单元体的三个棱边成某种比例,由于三个棱边应变相同,则变形后的三个棱边的长度仍保持这种比例.所以在三向等值应力m的作用下,单元体变形后的形状和变形前的相似,称这样的单元体是形状不变的.例题10边长a=0.1m的铜立方块,无间隙地放入体积较大,变形可略去不计的钢凹槽中,如图所示.已知铜的弹性模量E=100GPa,泊松比μ=0.34,当受到F=300kN的均布压力作用时,求该铜块的主应力,体积应变以及最大切应力.解得例题11一直径d=20mm的实心圆轴,在轴的的两端加扭矩Me=126N·m.在轴的表面上某一点A处用变形仪测出与轴线成
-45°方向的应变=5.010-4,试求此圆轴材料的剪切弹性模量G.解:围绕A点取一单元体解:从圆筒表面K点处取出单元体,其各面上的应力分量如图所示可求得K点处的线应变x,y为解:梁为拉伸与弯曲的组合变形.A点有拉伸引起的正应力和弯曲引起的切应力.（2）A点处的线应变x,y,z例题14简支梁由18号工字钢制成.其上作用有力F=15kN,已知E=200GPa,=0.3.解:§7-7复杂应力状态的应变能密度
(Strain-energydensityingeneralstress-state)将广义胡克定律代入上式,经整理得a单元体的比能为一、强度理论的概念（Conceptsoffailurecriteria)（2）材料的许用应力,是通过拉（压）试验或纯剪试验测定试件在破坏时其横截面上的极限应力,以此极限应力作为强度指标,除以适当的安全因数而得,即根据相应的试验结果建立的强度条件.基本观点（1）脆性断裂:无明显的变形下突然断裂.根据:当作用在构件上的外力过大时，其危险点处的材料就会沿最大拉应力所在截面发生脆断破坏.2.最大伸长线应变理论（第二强度理论）
（Maximum-normal-straincriterion）1.最大切应力理论（第三强度理论）
（Maximum-shear-stresscriterion）2.畸变能密度理论（第四强度理论