马尔科夫链.pptx

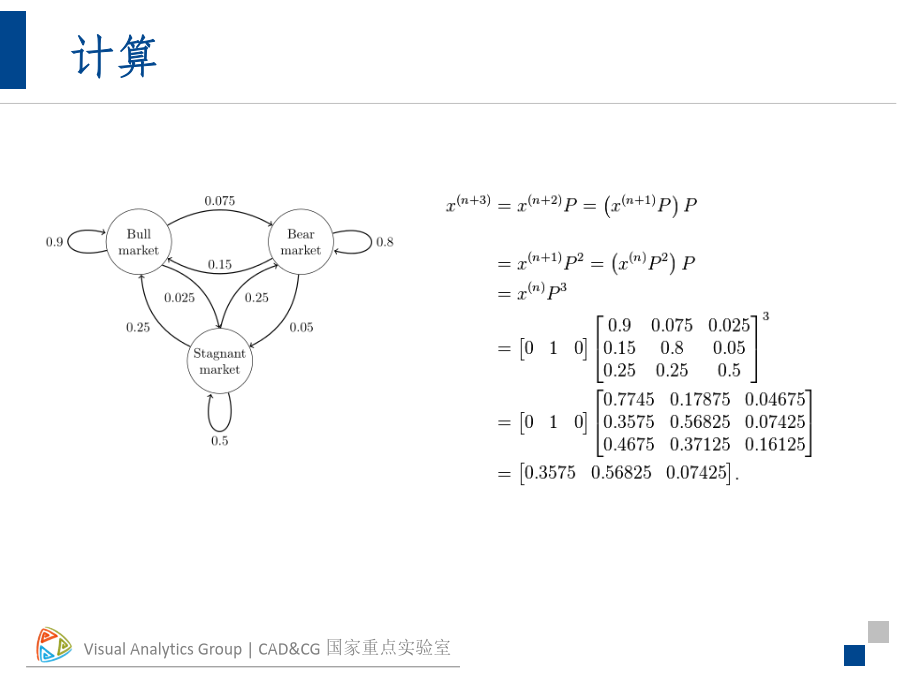
Марков/Markov的几个模型06-10月-24定义计算一个隐士不能直接观察天气来预测天气,但是他有一些水藻.民间传说,水藻的状态与天气有一定关系
于是有了两组状态:
观测状态——水藻的状态
隐藏状态——天气状况HiddenMarkovModel,HMMHiddenMarkovModel,HMM初始状态的概率向量
(隐)状态的转移矩阵
混淆矩阵
假设所有状态转移概率和混淆概率在整个系统中都是一成不变的1.评估:根据已知的HMM找出一个观测序列的概率
2.解码:根据观察序列找到最有可能出现的隐状态序列
3.学习:从观察序列中得出HMM背景:穷举法计算某一观察序列的概率部分概率:达到观察状态序列并且为一定状态j的概率最后的观察状态的部分概率表示这些状态所经过的所有可能路径的概率.最后的部分概率的和即为网络中所有可能路径的和,也就是当前HMM下观察序列的概率定义长度为T的观察序列为

初始状态(t=1)部分概率:

t>1时部分概率:部分概率:达到观察状态序列并且为一定状态j的概率我们可以通过穷举的方式列出所有可能隐含状态序列，并算出每一种隐状态序列组合对应的观察状态序列的概率。最有可能的隐状态序列是使得概率：
Pr(dry,damp,soggy|sunny,sunny,sunny),Pr(dry,damp,soggy|sunny,sunny,cloudy),Pr(dry,damp,soggy|sunny,sunny,rainy),....Pr(dry,damp,soggy|rainy,rainy,rainy)得到最大值的序列。
核心原理:如果最优路径在时刻t通过结点,那么这一路径从结点到终点的部分路径,对于从到所有可能的部分路径来说,必须是最优的.

对于网格中的每一个中间及终止状态,都有一个到达该状态的最可能路径.举例来说,在t=3时刻的3个状态中的每一个都有一个到达此状态的最可能路径,比如我们将这些路径称为局部最佳路径,其对应一个概率令是t时刻达到状态i的所有序列概率中最大的概率.

同样的,当t=1时,t>1时,我们考虑如下网络

假如A—X这样一条路径,那么定是
Pr(到达状态A最可能的路径)·Pr(X|A)·Pr(观察状态|X)
泛化该公式,即为我们计算每一步这样的最大值之后,还需要一个记录这样路径的方式.定义一个反向指针
又叫前向-后向算法,就是用来估计HMM参数的.
前面的局部概率改名前向变量:
类似的定义一个后向变量它可以用类似于前向算法那种递归的方式计算对于给定观察序列O,没有任何一种方法可以精确的找到一组最优的HMM参数(A,B,)使得Pr(O|).
定义两个变量:

若对于时间轴t上所有相加,我们可以得到一个总和，它可以被解释为从其他隐藏状态访问的期望值.
相似地,如果对在时间轴t上求和(从t=1到t=T-1),那么该和可以被解释为从状态到状态的状态转移期望值.06-10月-24输入法