
高中数学 第三章 统计案例 2 独立性检验教案 北师大版选修2-3-北师大版高二选修2-3数学教案.doc

Wi****m7



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

高中数学 第三章 统计案例 2 独立性检验教案 北师大版选修2-3-北师大版高二选修2-3数学教案.doc
2独立性检验一、教学目标:1、通过对典型案例的探究,了解独立性检验(只要求列联表)的基本思想、方法及初步应用;2、经历由实际问题建立数学模型的过程,体会其基本方法。二、教学重点、难点:独立性检验的基本方法是重点.基本思想的领会及方法应用是难点。三、教学方法:讨论交流,探析归纳四、教学过程(一)、问题情境5月31日是世界无烟日。有关医学研究表明,许多疾病,例如:心脏病、癌症、脑血管病、慢性阻塞性肺病等都与吸烟有关,吸烟已成为继高血压之后的第二号全球杀手。这些疾病与吸烟有关的结论是怎样得出的呢?我们看一下问题

高中数学 第三章 统计案例 3.2.1 独立性检验教案 北师大版选修2-3-北师大版高二选修2-3数学教案.doc
2.1独立性检验课标要求通过对典型案例的探究了解独立性检验(只要求列联表)的基本思想、方法及初步应用;三维目标1.知识与技能通过对典型案例的探究进一步了解回归分析的基本思想、方法和初步应用..2.过程与方法经历由实际问题建立数学模型的过程体会其基本方法.3.情感、态度与价值观体会回归分析在生产实际和日常生活中的广泛应用.教材分析回归分析主要是研究两个变量间的关系是在必修三的基础上学习回归分析是复习必修三的内容教师可通过实例让学生了解相关系数的大小与线性相关的关系;在现实中又有一种非线性的相关性如何解

高中数学 第三章 统计案例 2 独立性检验的应用教案 北师大版选修2-3-北师大版高二选修2-3数学教案.doc
2独立性检验的应用一、教学目标通过对典型案例的探究进一步巩固独立性检验的基本思想、方法并能运用统计量进行独立性检验。二、教学重点难点:独立性检验的基本方法是重点.基本思想的领会及方法应用是难点.三、教学方法:讨论交流探析归纳四、教学过程(一)、学生活动练习:(1)某大学在研究性别与职称(分正教授、副教授)之间是否有关系你认为应该收集哪些数据?.(2)某高校“统计初步”课程的教师随机调查了选该课的一些学生情况具体数据如下表:专业性别非统计专业统计专

高中数学 第三章 统计案例 2 独立性检验的应用教案 北师大版选修2-3-北师大版高二选修2-3数学教案.doc
2独立性检验的应用一、教学目标通过对典型案例的探究,进一步巩固独立性检验的基本思想、方法,并能运用统计量进行独立性检验。二、教学重点,难点:独立性检验的基本方法是重点.基本思想的领会及方法应用是难点.三、教学方法:讨论交流,探析归纳四、教学过程(一)、学生活动练习:(1)某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集哪些数据?.(2)某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:专业性别非统计专业统计专业男1310女720为了判断主修统计专业是否与性
高中数学 第三章 统计案例 3.2.3 独立性检验的应用教案 北师大版选修2-3-北师大版高二选修2-3数学教案.doc
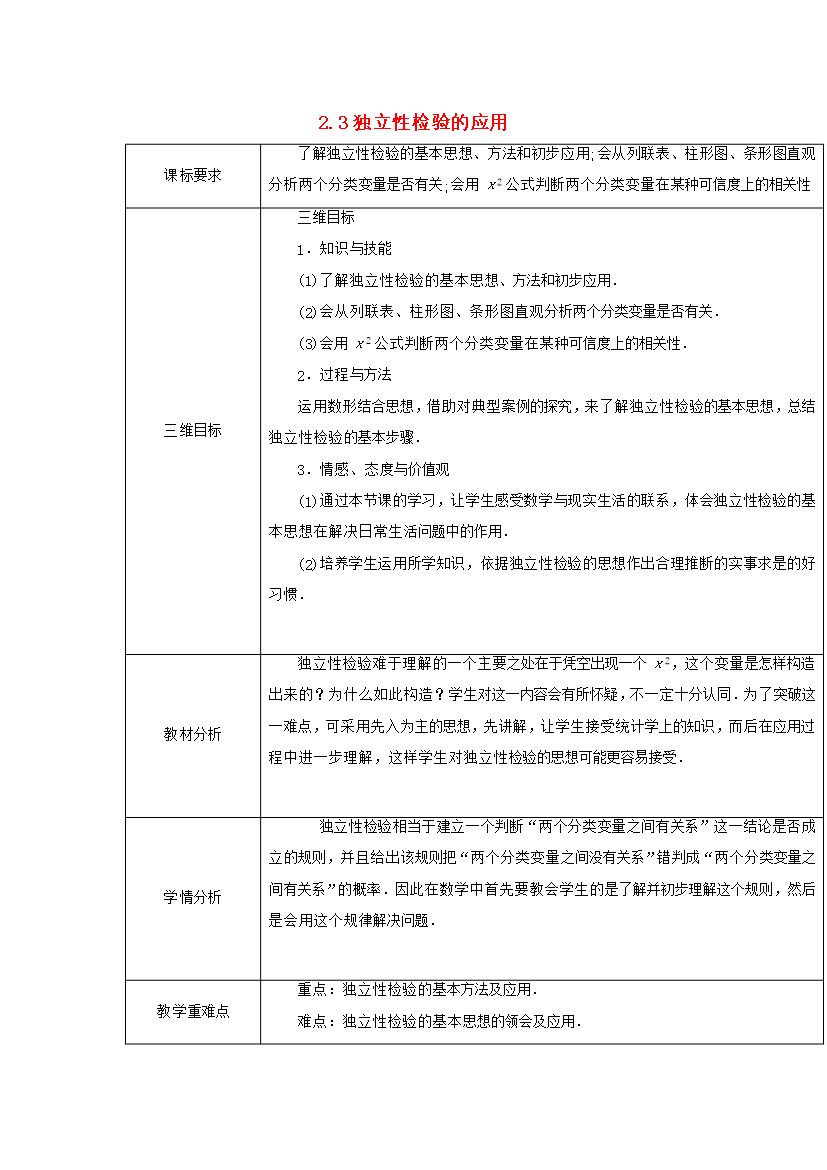
2.3独立性检验的应用课标要求了解独立性检验的基本思想、方法和初步应用;会从列联表、柱形图、条形图直观分析两个分类变量是否有关;会用χ2公式判断两个分类变量在某种可信度上的相关性三维目标三维目标1.知识与技能(1)了解独立性检验的基本思想、方法和初步应用.(2)会从列联表、柱形图、条形图直观分析两个分类变量是否有关.(3)会用χ2公式判断两个分类变量在某种可信度上的相关性.2.过程与方法运用数形结合思想借助对典型案例的探究来了解独立性检验的基本思想总结独立性检验的基本步骤.3.情感、态度与价值观(1)通过
