主成分分析法.ppt

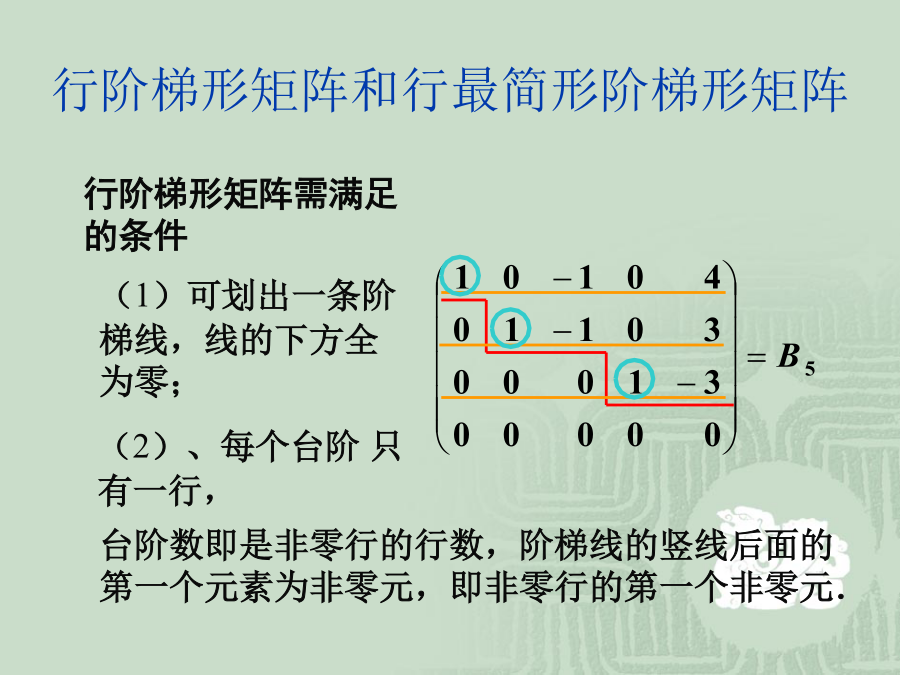
第七章地理系统的主成分分析（PrincipalComponentAnalysis）线性代数知识补充定义1行阶梯形矩阵和行最简形阶梯形矩阵注意：行最简形矩阵是由方程组唯一确定的，行阶梯形矩阵的行数也是由方程组唯一确定的．主成分分析问题的提出
地理系统是多要素的复杂系统。在地理学研究中，多变量问题是经常会遇到的。变量太多，无疑会增加分析问题的难度与复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的。
因此，人们会很自然地想到，能否在相关分析的基础上，用较少的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来变量所反映的信息？事实上，这种想法是可以实现的，主成分分析方法就是综合处理这种问题的一种强有力的工具。
主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。
从数学角度来看，这是一种降维处理技术。

一、主成分分析的基本原理当p较大时，在p维空间中考察问题比较麻烦。为了克服这一困难，就需要进行降维处理，即用较少的几个综合指标代替原来较多的变量指标，而且使这些较少的综合指标既能尽量多地反映原来较多变量指标所反映的信息，同时它们之间又是彼此独立的。定义：记x1，x2，…，xP为原变量指标，z1，z2，…，zm（m≤p）为新变量指标
②z1是x1，x2，…，xP的一切线性组合中方差最大者，z2是与z1不相关的x1，x2，…，xP的所有线性组合中方差最大者;…;zm是与z1，z2，……，zm－1都不相关的x1，x2，…xP，的所有线性组合中方差最大者。

则新变量指标z1，z2，…，zm分别称为原变量指标x1，x2，…，xP的第1，第2，…，第m主成分。
从以上的分析可以看出，主成分分析的实质就是确定原来变量xj（j=1，2，…，p）在诸主成分zi（i=1，2，…，m）上的荷载lij（i=1，2，…，m；j=1，2，…，p）。
从数学上可以证明，它们分别是相关矩阵m个较大的特征值所对应的特征向量。二、主成分分析的计算步骤（二）计算特征值与特征向量
①解特征方程，常用雅可比法（Jacobi）求出特征值，并使其按大小顺序排列；③计算主成分贡献率及累计贡献率
贡献率④计算主成分载荷

⑤各主成分的得分

三、主成分分析方法应用实例步骤如下：
（1）将表中的数据作标准差标准化处理，然后将它们代入公式,计算相关系数矩阵，如表7.2所示.
（2）由相关系数矩阵计算特征值，以及各个主成分的贡献率与累计贡献率（表7.3）。由表7.3可知，第1，第2，第3主成分的累计贡献率已高达86.596%（大于85%），故只需要求出第1、第2、第3主成分z1，z2，z3即可。表7.3特征值及主成分贡献率（3）对于特征值=4.6610，=2.0890，=1.0430分别求出其特征向量e1，e2，e3，再用公式计算各变量x1，x2，…，x9在主成分z1，z2，z3上的载荷（表7.4）。表7.4主成分载荷(1)第1主成分z1与x1，x5，x6，x7，x9呈现出较强的正相关，与x3呈现出较强的负相关，而这几个变量则综合反映了生态经济结构状况，因此可以认为第1主成分z1是生态经济结构的代表。
(2)第2主成分z2与x2，x4，x5呈现出较强的正相关，与x1呈现出较强的负相关，其中，除了x1为人口总数外，x2，x4，x5都反映了人均占有资源量的情况，因此可以认为第2主成分z2代表了人均资源量。
显然，用3个主成分z1、z2、z3代替原来9个变量（x1，x2，…，x9）描述农业生态经济系统，可以使问题更进一步简化、明了。