基于超椭圆曲线的轮盘异型孔结构设计方法.pdf

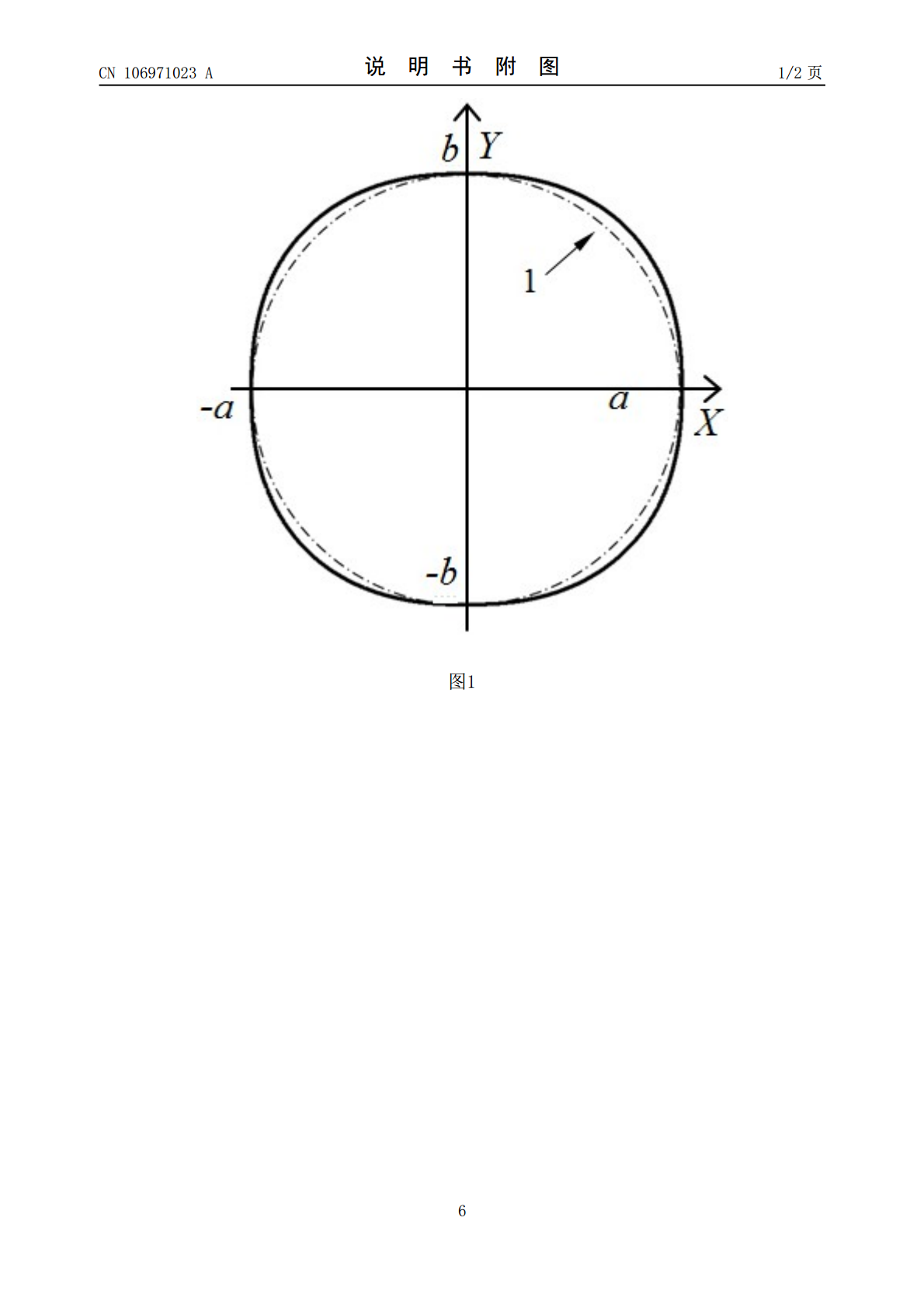
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN106971023A(43)申请公布日2017.07.21(21)申请号201710117739.4(22)申请日2017.03.01(71)申请人南京航空航天大学地址210016江苏省南京市秦淮区御道街29号(72)发明人郭海丁韩佳欣殷良伟王佳(74)专利代理机构江苏圣典律师事务所32237代理人贺翔(51)Int.Cl.G06F17/50(2006.01)权利要求书1页说明书3页附图2页(54)发明名称基于超椭圆曲线的轮盘异型孔结构设计方法(57)摘要本发明提供了一种基于超椭圆曲线的轮盘异型孔结构设计方法，用于解决目前轮盘孔结构的孔边应力集中问题，提高了设计结果的实用性，简化了异型孔结构的设计过程。技术方案是采用超椭圆曲线对轮盘孔类结构进行改进；构建一种超椭圆异型孔多目标优化模型，使超椭圆异型孔轮廓同时满足两个优化目标：1）孔边应力水平降低到设置水平2）孔形状变化尽可能小以满足传力要求；该模型可通过优化获得最佳设计。优化得到的超椭圆孔可按设计者需求将孔边最大应力降低10%~20%，且异型孔轮廓形状与先前圆孔的差异度较小，可满足原有的装配，保证传力可靠。此外，该方法所需设计变量较少，异型孔轮廓的数学模型简洁。CN106971023ACN106971023A权利要求书1/1页1.一种基于超椭圆曲线的轮盘异型孔结构设计方法，其特征在于包括以下步骤：步骤一、定义超椭圆异型孔曲线方程：式中，a、b为超椭圆曲线的半轴值，m、n为指数；步骤二、采用超椭圆参数方程运用有限元分析软件进行参数化建模：式中，θ为参数，sgn为符号判断函数：步骤三、构建超椭圆异型孔多目标优化模型：minf{f1(σmax),f2(m,n)}；(4)其中，优化设计变量m、n为超椭圆曲线指数；σmax＝σmax(m,n)为设计点λ(m,n)对应的超椭圆孔孔边最大主应力值，目标函数f1(σmax)代表孔边应力降低程度；目标函数f2(m,n)代表超椭圆异型孔轮廓变化；upper和lower分别为曲线指数的上、下界；步骤四、运用多目标优化方法对超椭圆异型孔优化模型进行寻优，最终得到异型孔轮廓优化结果。2.根据权利要求1所述的一种基于超椭圆曲线的轮盘异型孔结构设计方法，其特征在于：步骤一中，m，n>2。3.根据权利要求1所述的一种基于超椭圆曲线的轮盘异型孔结构设计方法，其特征在于：步骤三中，目标函数f2(m,n)计算方法如方程如下所示：f2(m,n)＝S1-S0。(6)S1为超椭圆异型孔面积，S0为原圆孔面积。2CN106971023A说明书1/3页基于超椭圆曲线的轮盘异型孔结构设计方法技术领域[0001]本发明涉及航空发动机涡轮转子部件的孔类结构优化设计领域，具体是一种基于超椭圆曲线的轮盘异型孔结构设计方法。背景技术[0002]航空发动机涡轮转子部件工作环境恶劣，其轮盘幅板上的螺栓孔、通气孔等孔类结构常因应力集中现象，产生孔边裂纹，成为轮盘失效的一个重要原因。传统措施如采用孔边倒角、抛光、增加结构重量等方法并不能从根本上解决该问题。发明内容[0003]本发明为了解决现有技术的问题，提供了一种基于超椭圆曲线的轮盘异型孔结构设计方法，按结构使用需求降低孔边应力，同时保证孔轮廓形状变化尽可能小，以此满足强度要求、装配要求并保证可靠传力。该方法所需设计变量较少，异型孔数学模型简洁。[0004]本发明包括以下步骤：[0005]步骤一、定义超椭圆异型孔曲线方程。[0006][0007]式中，a、b为超椭圆曲线的半轴值，m、n为指数，其取值不同，超椭圆异型孔形状不同，此发明中取m，n>2，此时异型孔轮廓介于方孔和圆孔之间，更加符合轮盘孔类结构的实际设计要求。[0008]步骤二、采用超椭圆参数方程运用有限元分析软件进行参数化建模：[0009][0010]式中，θ为参数，sgn为符号判断函数：[0011][0012]步骤三、构建超椭圆异型孔多目标优化模型：[0013]minf{f1(σmax)，f2(m,n)}；(4)[0014][0015]其中，优化设计变量m、n为超椭圆曲线指数；σmax＝σmax(m,n)为设计点λ(m,n)对应的超椭圆孔孔边最大主应力值，目标函数f1(σmax)代表孔边应力降低程度；目标函数f2(m,n)代表超椭圆异型孔轮廓变化；upper和lower分别为曲线指数的上、下界；3CN106971023A说明书2/3页[0016]目标函数f2(m,n)计算方法如方程如下所示：[0017]f2(m,n)＝S1-S0。(6)[0018]S1为超椭圆异型孔面积，S0为原圆孔面积。[0019]步骤四、运用多目标优化方法对超椭圆异型孔优化模型进行寻优，最终得到异型孔轮廓优化结果。[0020]本发明有益