微弱信号检测ppt课件.ppt

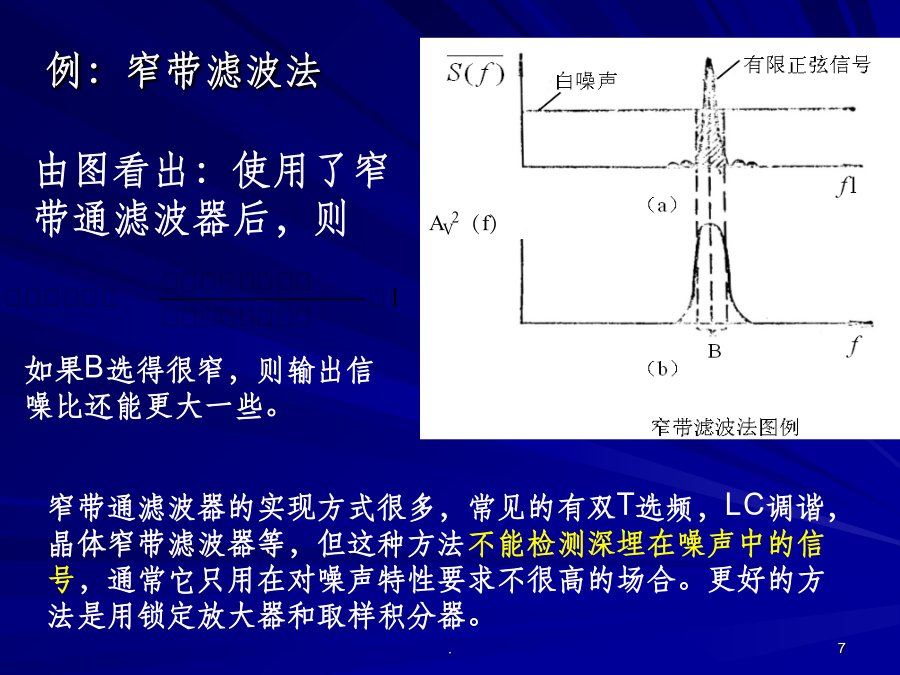
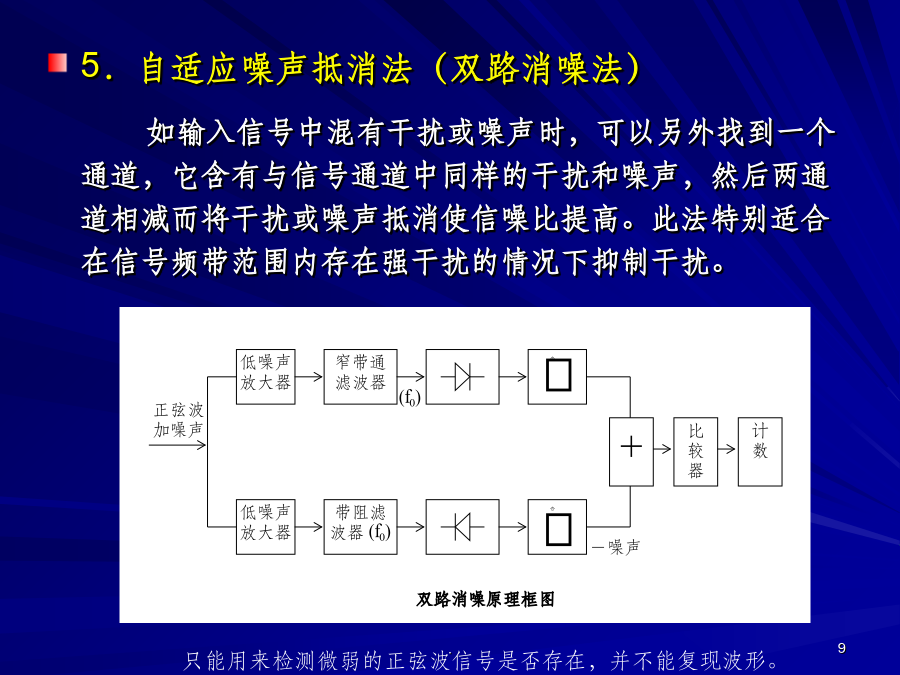
4.3.0概述4.3.1信噪比改善（SNIR） 4.3.2相关检测原理 4.3.3锁定放大器 4.3.4取样积分器 4.3.0概述一.微弱信号检测定义微弱信号检测定义：利用电子学、信息论和物理学的方法，分析噪声产生的规律找到抑制的方法；研究被测信号的特点和相干性，检测被背景噪声淹没的弱信号。
微弱信号检测是测量技术中的尖端和综合领域，可划归“低噪声电子学”。二.微弱信号检测的途径1．时域相关与频域的窄带化技术
利用时域中周期信号的相关性而噪声的随机、不相关性（或弱相关性），通过求取信号的自相关函数或互相关函数，在强噪声背景下提取周期信号的“相关检测”。这相当于在频率中窄带化滤除干扰和噪声。特别适用窄带信号。例如锁定放大器。

2．平均积累处理
对于一些宽带周期信号应用上述方法处理效果不佳，一种根据时域特征用取样平均来改善信噪比并能恢复波形的取样积分器可获得良好探测效果。其基本原理是对于任何重复的（周期性）信号波形，每周期如在固定的取样间隔内取样m次积累则信噪比改善。因为“信号电压幅值为线性叠加”（有规律的周期信号）而“噪声功率为矢量相加”（无规律的随机信号）。例：窄带滤波法3．离散量的统计计数技术
用PMT（宽带低噪声前放、甄别器和计数器等电路完成）实现光子计算。
4．单次信息的并行检测技术
对于那些只有一次事件的信息记录，如对一个非周期信号的检测，可采用并行检测技术。实现并行检测需要一个探测阵列，其中每个探测器必须有存贮的功能，且可以依次将存贮的信息读出，再进行信号处理，一般采用多路传输和多道技术。典型例子：光学多通道分析器（OMA－OpticalMultichannelAnalyzer）。5．自适应噪声抵消法（双路消噪法）
如输入信号中混有干扰或噪声时，可以另外找到一个通道，它含有与信号通道中同样的干扰和噪声，然后两通道相减而将干扰或噪声抵消使信噪比提高。此法特别适合在信号频带范围内存在强干扰的情况下抑制干扰。可供选用的弱检仪器，目前有如下几种：
低噪声前放；
各种锁定放大器（LIA）；
各种取样积分器（Boxcar）；
多点信号平均器；
光子计数器；
光多通道分析仪（OMA）4.3.1信噪比改善（SNIR）3dB带宽等效噪声带宽角频率表示时间常数相同的RC网络等效噪声带宽比3dB带宽要宽：噪声是一种平稳随机信号；
噪声一般采用长周期测定其均方值(即噪声功率)的方法，通常采用先计算噪声电压(电流)的平方值，然后将其对时间作平均，来求噪声电压(电流)的均方值，即：表示频率在f与f+∆f之间的噪声频谱分量的平均功率设输入端的噪声功率谱密度为Si（f），则输出端的噪声功率谱密度S0（f）为：根据噪声功率谱的含义，那么线性网络输出端的噪声电压均方值(即输出的噪声功率)为：信噪比改善（SNIR－SignalNoiseImprovementRatio）是衡量弱检仪器的一项重要性能指标。
信噪比改善的定义为从数学表达式看，SNIR似乎是噪声系数F的倒数，但实质上两者是有差别的:
●噪声系数仅适用于不采取带宽限制的信号源加前置放大器的系统；并且得到结论F≥1。这个结论的产生是由于假设了输入噪声的带宽等于或小于放大系统的噪声带宽。
●对整个信号处理系统而言，实际上输入噪声的带宽要大于整个信号处理系统的带宽，因而噪声系数F便有可能要小于1，不适宜描述整个系统，因此而给出信噪比改善的概念。
Eni是等效输入宽带白噪声电压，其功率谱密度S(f)为常数，输入噪声带宽为Δfin，放大系统的信噪比改善：
等于输入噪声的带宽Δfin与系统的等效噪声带宽Δfn之比。
因此，减小系统的等效噪声带宽，可以提高信噪比改善。
由此可见，那么只要检测放大系统的等效噪声带宽做得很小，使Δfn<<Δfni，就可能将此信号检测出来。例：窄带滤波法4.3.2相关检测原理
为了将被噪声所淹没的信号检测出来，人们研究各种信号及噪声的规律，发现信号与信号的延时相乘后累加的结果可以区别于信号与噪声的延时相乘后累加的结果，从而提出了“相关”的概念。
由于相关的概念涉及信号的能量及功率，因此先给出功率信号和能量信号的相关函数。f1(t)与f2(t)是能量有限信号
f1(t)与f2(t)为实函数
f1(t)与f2(t)为复函数
f1(t)与f2(t)是功率有限信号
f1(t)与f2(t)为实函数
f1(t)与f2(t)为复函数1.f1(t)与f2(t)是能量有限信号互相关函数：互相关函数：Rxy(τ)＝Ryx(－τ)，即Rxy(τ)与Ryx(τ)互为镜像对称。
如果两个信号或随机过程互相完全没有关系，（例如信号与噪声）则其互相关函数将为一个常数，并且等于两个信号平均值的乘积；若其中一个（如噪声）的平均值为零，则它们的互相关函数Rxy(τ)将处处为零，即完全不相关。
如果两个信号是具有相同