第2章01--流密码(LFSR).ppt

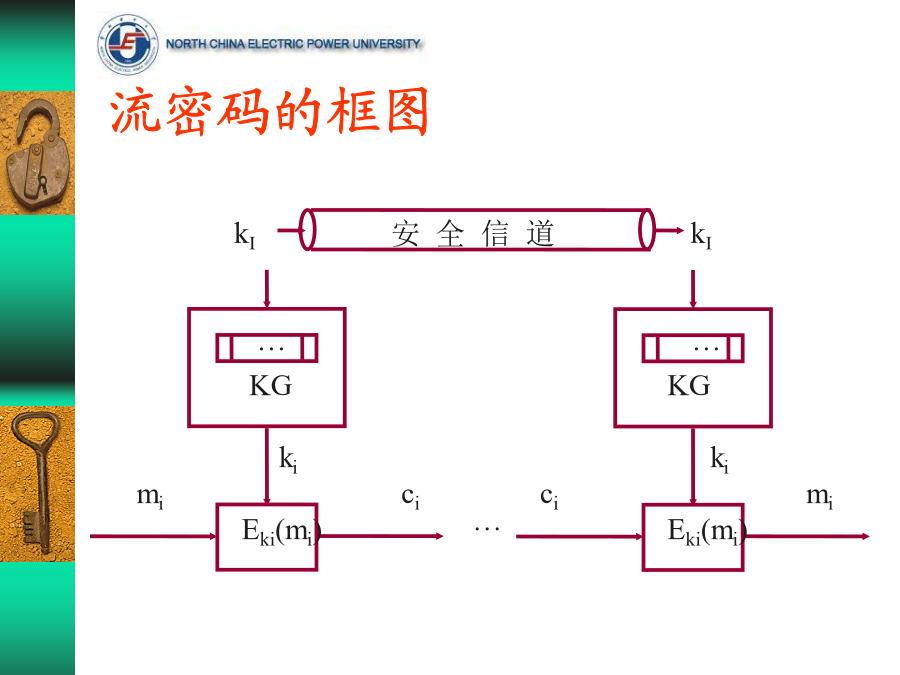
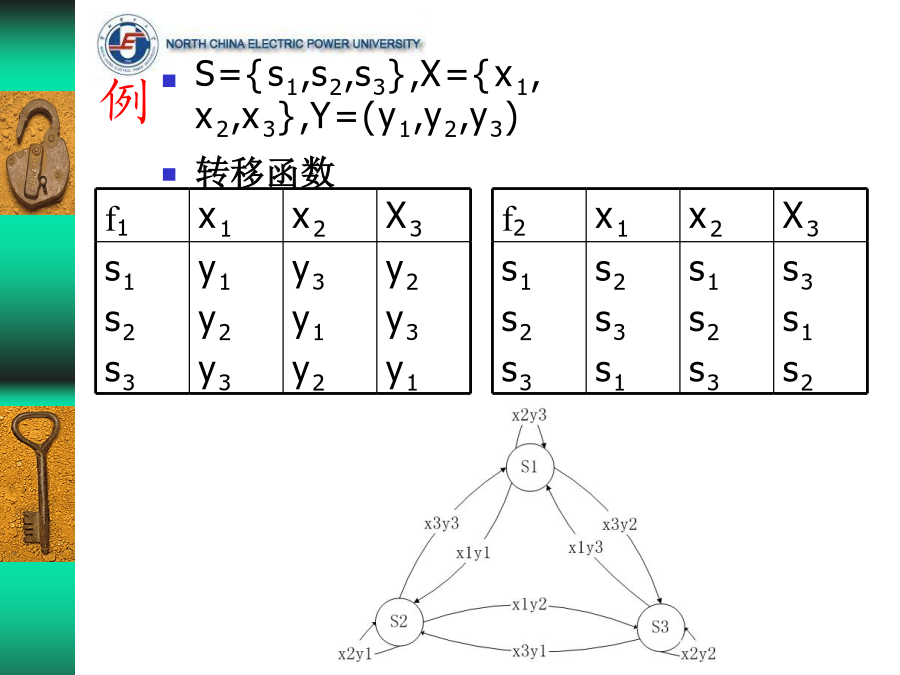
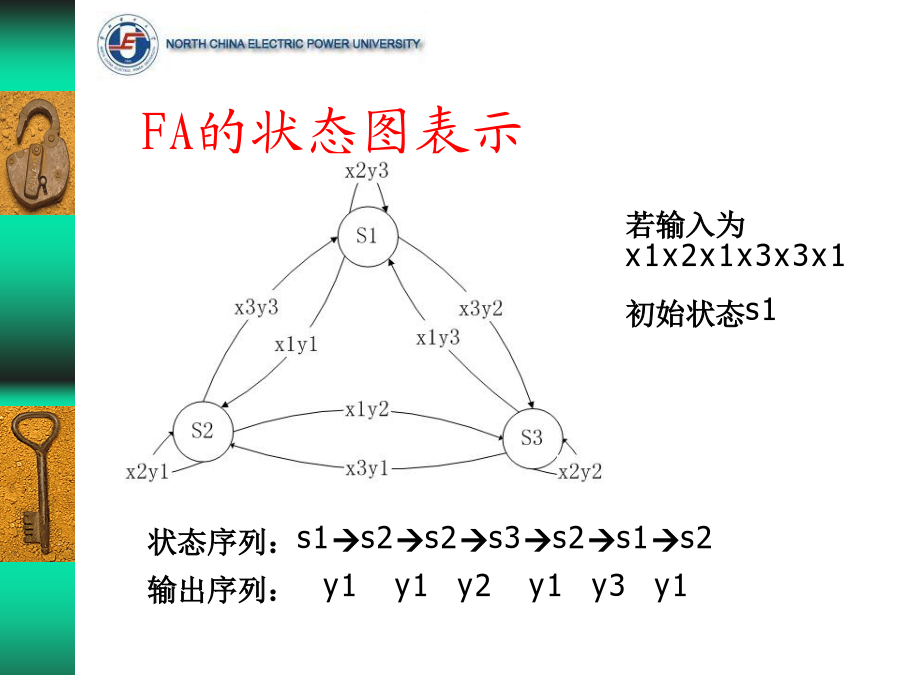
第2章流密码(序列密码)流密码的基本概念流密码的框图流密码的框图流密码的分类(1)流密码的分类(2)同步流密码有限状态自动机FA(FinitestateAutomation)例FA的状态图表示作为FA的密钥流产生器作为FA的密钥流产生器两种常见的密钥流产生器第四章流密码线性反馈移位寄存器序列概念例：3级反馈移位寄存器，其初始状态为(a1,a2,a3)=(1,0,1)，输出可由表求出如果移位寄存器的反馈函数f(a1,a2,…,an)是a1，a2，…，an的线性函数，则称之为线性反馈移位寄存器LFSR（linearfeedbackshiftregister）。
此时f可写为

其中常数ci=0或1，是模2加法。

ci=0或1可用开关的断开和闭合来实现，如上图所示。输出序列{at}满足
an+t=cnatcn-1at+1…c1an+t-1
其中t为非负正整数。

线性反馈移位寄存器因其实现简单、速度快、有较为成熟的理论等优点而成为构造密钥流生成器的最重要的部件之一。例，下图是一个5级线性反馈移位寄存器，其初始状态为（a1,a2,a3,a4,a5）=(1,0,0,1,1)，可求出输出序列为：在线性反馈移位寄存器中总是假定c1,c2,…,cn中至少有一个不为0，否则f(a1,a2,…,an)≡0，这样的话，在n个脉冲后状态必然是00…0，且这个状态必将一直持续下去。
若只有一个系数不为0，设仅有cj不为0，实际上是一种延迟装置。一般对于n级线性反馈移位寄存器，总是假定c0=1。线性反馈移位寄存器输出序列的性质完全由其反馈函数决定。
n级线性反馈移位寄存器最多有2n个不同的状态。
若其初始状态为0，则其状态恒为0。若其初始状态非0，则其后继状态不会为0。
因此n级线性反馈移位寄存器的状态周期小于等于2n-1。
其输出序列的周期与状态周期相等，也小于等于2n-1。
只要选择合适的反馈函数便可使序列的周期达到最大值2n-1，周期达到最大值的序列称为m序列。第四章流密码设n级LFSR的输出序列满足递推关系
an+k=c1an+k-1c2an+k-2…cnak(*)
对任何k≥1成立。这种递推关系可用一个一元高次多项式
P(x)=1+c1x+…＋cn-1xn-1＋cnxn
表示，称这个多项式为LFSR的特征多项式。
实例：（画出下列个移存器的逻辑框图，写出相应的线性递推式，并讨论由它们所产生的序列）
答案：
1、该移存器产生三类周期相同（全为5）的序列及一个全零序列。
2、该移存器产生五类周期分别为6、3、3、2、1的序列及一个全零序列。
3、该移存器产生周期为15的m序列及一个全零序列。本原多项式例：本原多项式例：（32，7，5，3，2，1，0）

一些本原多项式: