因子分析原理ppt课件.ppt

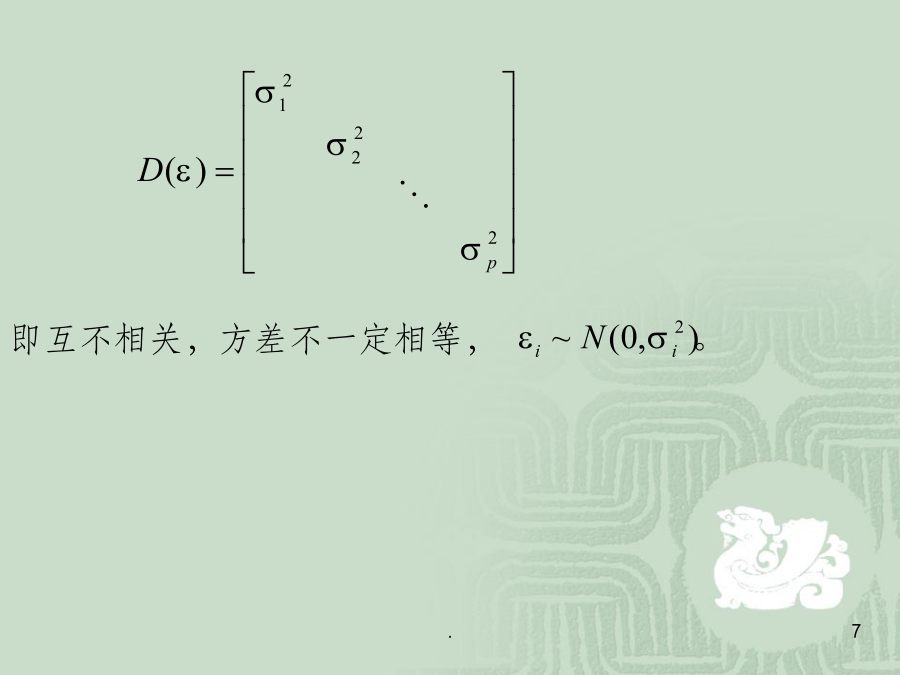
因子分析§1引言
因子分析(factoranalysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。
例如，在企业形象或品牌形象的研究中，消费者可以通过一个有24个指标构成的评价体系，评价百货商场的24个方面的优劣。但消费者主要关心的是三个方面，即商店的环境、商店的服务和商品的价格。因子分析方法可以通过24个变量，找出反映商店环境、商店服务水平和商品价格的三个潜在的因子，对商店进行综合评价。而这三个公共因子可以表示为：注：
因子分析与回归分析不同，因子分析中的因子是一个比较抽象的概念，而回归因子有非常明确的实际意义；
主成分分析分析与因子分析也有不同，主成分分析仅仅是变量变换，而因子分析需要构造因子模型。
主成分分析:原始变量的线性组合表示新的综合变量，即主成分；
因子分析：潜在的假想变量和随机影响变量的线性组合表示原始变量。§2因子分析模型称为公共因子，是不可观测的变量，他们的系数称为因子载荷。是特殊因子，是不能被前m个公共因子包含的部分。并且满足：即互不相关，方差不一定相等，。用矩阵的表达方式二、因子分析模型的性质2、模型不受计量单位的影响113、因子载荷不是惟一的三、因子载荷矩阵中的几个统计特征
2、变量共同度的统计意义
3、公共因子方差贡献的统计意义
§3因子载荷矩阵的估计方法上式给出的表达式是精确的，然而，它实际上是毫无价值的，因为我们的目的是寻求用少数几个公共因子解释，故略去后面的p-m项的贡献，有注：残差矩阵（二）主因子法直接求R*的前p个特征根和对应的正交特征向量。得如下
的矩阵：23在实际的应用中，个性方差矩阵一般都是未知的，
可以通过一组样本来估计。估计的方法有如下几种：
2）取，这意味着取xi与其余的xj的简单相关系数的绝对值最大者；
（三）极大似然估计法（略）它通过依赖和。上式并不能唯一确定,为此可添加一个唯一性条件：

这里式一个对角矩阵，用数值极大化的方法可以得
到极大似然估计。极大似然估计
将使为对角阵，且似然函数达到最大。
相应的共同度的似然估计为：

第J个因子对总方差的贡献：
例假定某地固定资产投资率，通货膨胀率，失业率，相关系数矩阵为

试用主成分分析法求因子分析模型。特征根为：可取前两个因子F1和F2为公共因子，第一公因子F1物价就业因子，对X的贡献为1.55。第一公因子F2为投资因子，对X的贡献为0.85。共同度分别为1，0.706，0.706。假定某地固定资产投资率，通货膨胀率，失业率，相关系数矩阵为

试用主因子分析法求因子分析模型。假定用
代替初始的。。特征根为：33§4因子旋转（正交变换）百米跑成绩
跳远成绩
铅球成绩
跳高成绩
400米跑成绩
百米跨栏
铁饼成绩
撑杆跳远成绩
标枪成绩
1500米跑成绩36因子载荷矩阵可以看出，除第一因子在所有的变量在公共因子上有较大的正载荷，可以称为一般运动因子。其他的3个因子不太容易解释。似乎是跑和投掷的能力对比，似乎是长跑耐力和短跑速度的对比。于是考虑旋转因子，得下表38通过旋转，因子有了较为明确的含义。百米跑，
跳远和400米跑，需要爆发力的项目在有较大的载荷，可以称为短跑速度因子；
铅球，铁饼和标枪在上有较大的载荷，可以称为爆发性臂力因子；
百米跨栏，撑杆跳远，跳远和为跳高在上有较大的载荷，爆发腿力因子；长跑耐力因子。
变换后因子的共同度变换后因子贡献1、方差最大法
方差最大法从简化因子载荷矩阵的每一列出发，使和每个因子有关的载荷的平方的方差最大。当只有少数几个变量在某个因子上又较高的载荷时，对因子的解释最简单。方差最大的直观意义是希望通过因子旋转后，使每个因子上的载荷尽量拉开距离，一部分的载荷趋于1，另一部分趋于0。4344451、四次方最大旋转
四次方最大旋转是从简化载荷矩阵的行出发，通过旋转初始因子，使每个变量只在一个因子上又较高的载荷，而在其它的因子上尽可能低的载荷。如果每个变量只在一个因子上又非零的载荷，这是的因子解释是最简单的。
四次方最大法通过使因子载荷矩阵中每一行的因子载荷平方的方差达到最大。473、等量最大法
等量最大法把四次方最大法和方差最大法结合起来求Q和V的加权平均最大。

§5因子得分人均要素变量因子分析。对我国32个省市自治区的要素状况作因子分析。指标体系中有如下指标：
X1：人口（万人）X2：面积（万平方公里）
X3：GDP（亿元）X4：人均水资源（立方米/人）
X5：人均生物量（吨/人）X6：万人拥有的大学生数（人）
X7：万人拥有科学家、工程师数（人）

Standard