
一种基于非凸低秩的动态MRI重建方法.pdf

宏硕****mo








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

一种基于非凸低秩的动态MRI重建方法.pdf
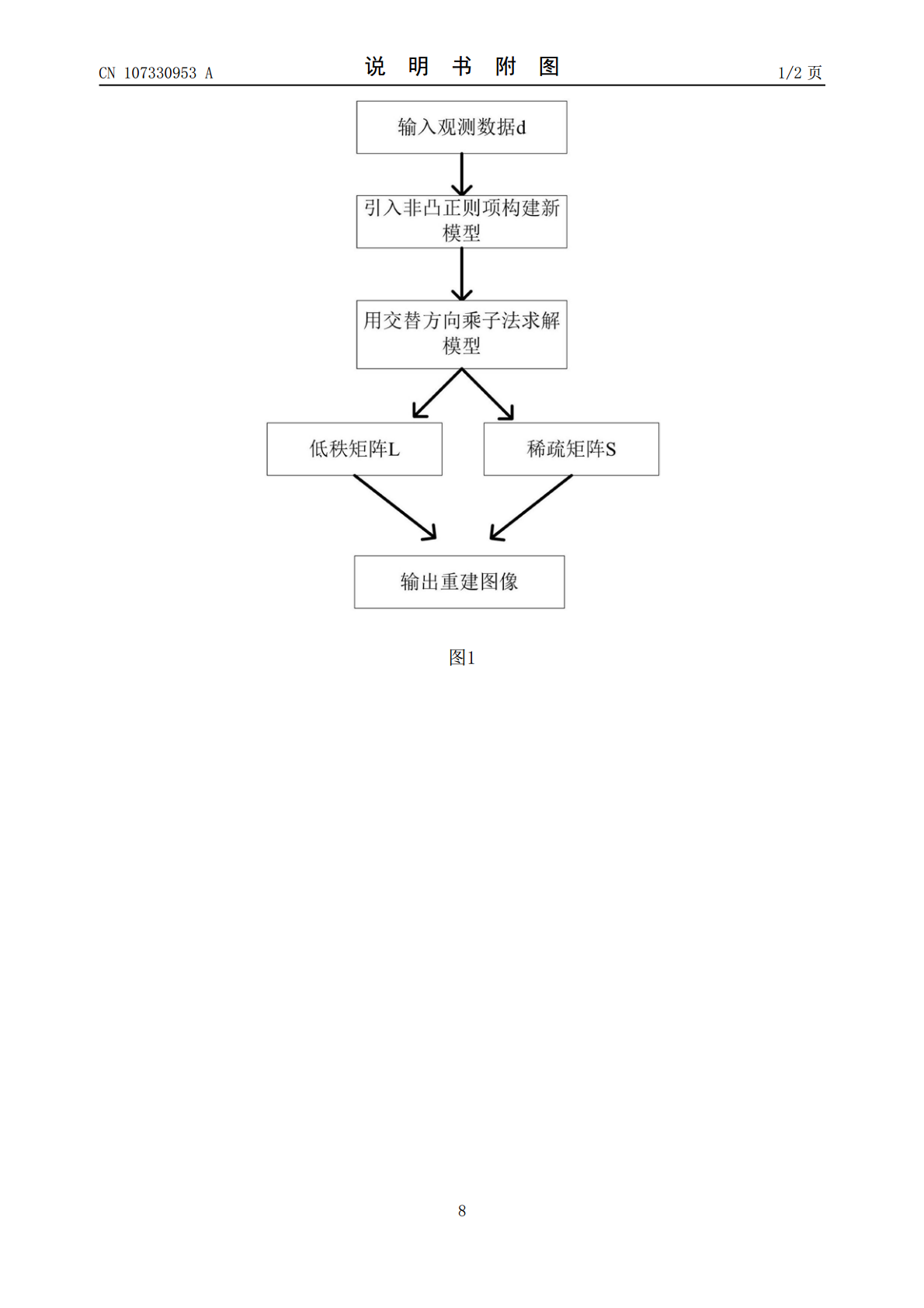
本发明公开一种基于非凸低秩的动态MRI重建方法,其将非凸正则项引入动态MRI的重建模型中,减少与真实值之间的误差,即在分离MR图像时,可以得到更精确的前景和背景。其次在视觉效果上,能够保留较多的纹理信息和轮廓信息,更便于病情的诊断。

基于低秩稀疏分解快速算法的动态MRI重建.pptx
,目录PartOnePartTwo动态MRI的应用领域动态MRI重建的挑战低秩稀疏分解在动态MRI重建中的重要性PartThree低秩稀疏分解算法的基本原理低秩稀疏分解算法在动态MRI重建中的应用低秩稀疏分解算法的优势和局限性PartFour算法流程和实现细节算法的时间复杂度和空间复杂度分析算法的优化策略和改进方向PartFive实验数据和实验环境介绍实验结果展示和分析与其他算法的性能对比和优势分析PartSix基于低秩稀疏分解快速算法的动态MRI重建的应用前景未来研究的方向和挑战THANKS

基于参考影像纹理约束和非凸低秩约束的遥感图像重建方法.pdf
本发明公开了一种基于参考影像纹理约束和广义非凸低秩核范数约束的遥感图像重建方法,包括以下步骤:S1设置目标影像稀疏系数初始值,计算参考影像小波子稀疏系数;S2根据纹理在小波变换域统计特性,计算目标影像和参考影像小波子影像纹理特征向量的Canberra距离,得到相似度;S3用非凸低秩核范数约束目标影像稀疏系数,将相似度加入目标影像的稀疏系数中进行更新,构建目标函数;和S4通过共轭梯度算法、局部最小化泰勒一阶近似和奇异值分解迭代求解带目标影像低秩先验信息的非局部遥感影像重建模型。本发明有益效果:将参考影像小波

一种用于磁共振快速成像的非凸低秩重建方法.pdf
一种用于磁共振快速成像的非凸低秩重建方法,本发明建立基于非局部相似图像块低秩先验信息的MR图像数据重构数学模型,釆用交替方向迭代方法对模型进行迭代求解:通过泰勒一阶近似和奇异值分解迭代求解带低秩先验信息的非局部图像模型的低秩矩阵的非凸p范数,得到相似图像块,再通过增加辅助变量和分离变量法迭代求解重建图像。本发明利用图像先验信息,将图像块的非局部相似性与低秩特性结合,并利用傅里叶变换和低秩矩阵的特性简化计算过程,降低算法复杂度,提高了部分K空间数据重建MRI图像的性能,在更少的扫描测量下更精确地重建图像,减

基于加权非凸正则化和迭代重约束低秩表示的动态视频分割方法.pdf
基于加权非凸正则化和迭代重约束低秩表示的动态视频分割方法,包括如下步骤:(1)针对误差矩阵引入加权因子W,确定权值矩阵的约束形式;(2)结合W矩阵计算空间Laplacian结构矩阵L;(3)针对表示矩阵Z的奇异值引入加权的非凸Rational函数;(4)通过步骤1、2和3优化现存GLRR框架,提出IRWNR模型;(5)采用IRM框架(算法1)迭代优化目标模型中的未知变量W、L和Z;(6)采用近端梯度(EIPG)算法(算法2)解决Z的子问题;(7)采用分块奇异值阈值逼近法(算法3)实现算法2中的SVT操作;
