
初中数学知识点-53、米勒最值问题.pdf

lj****88


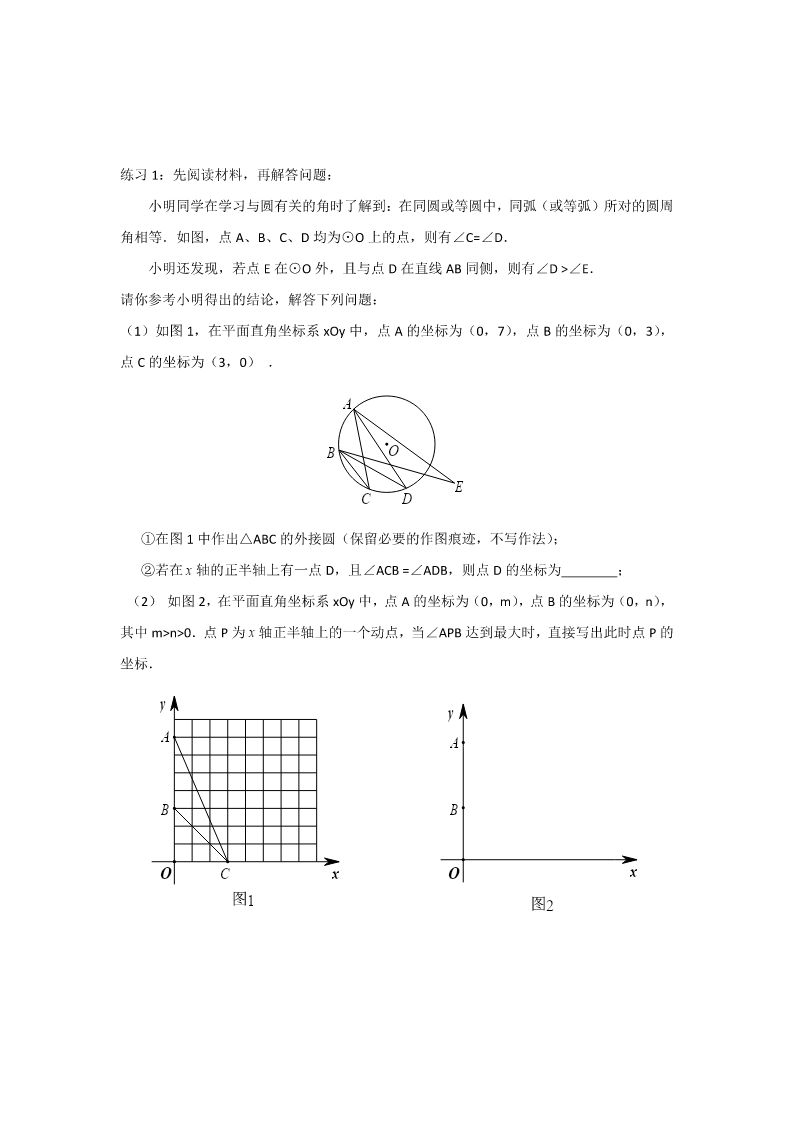

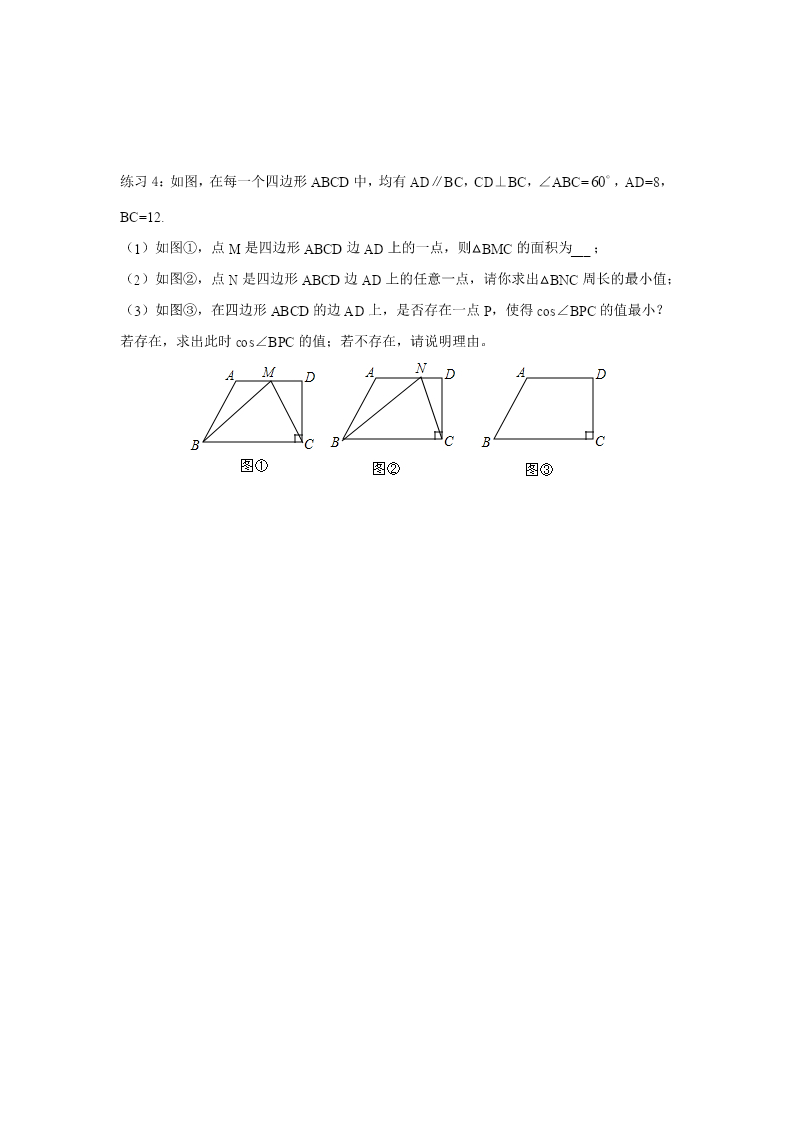
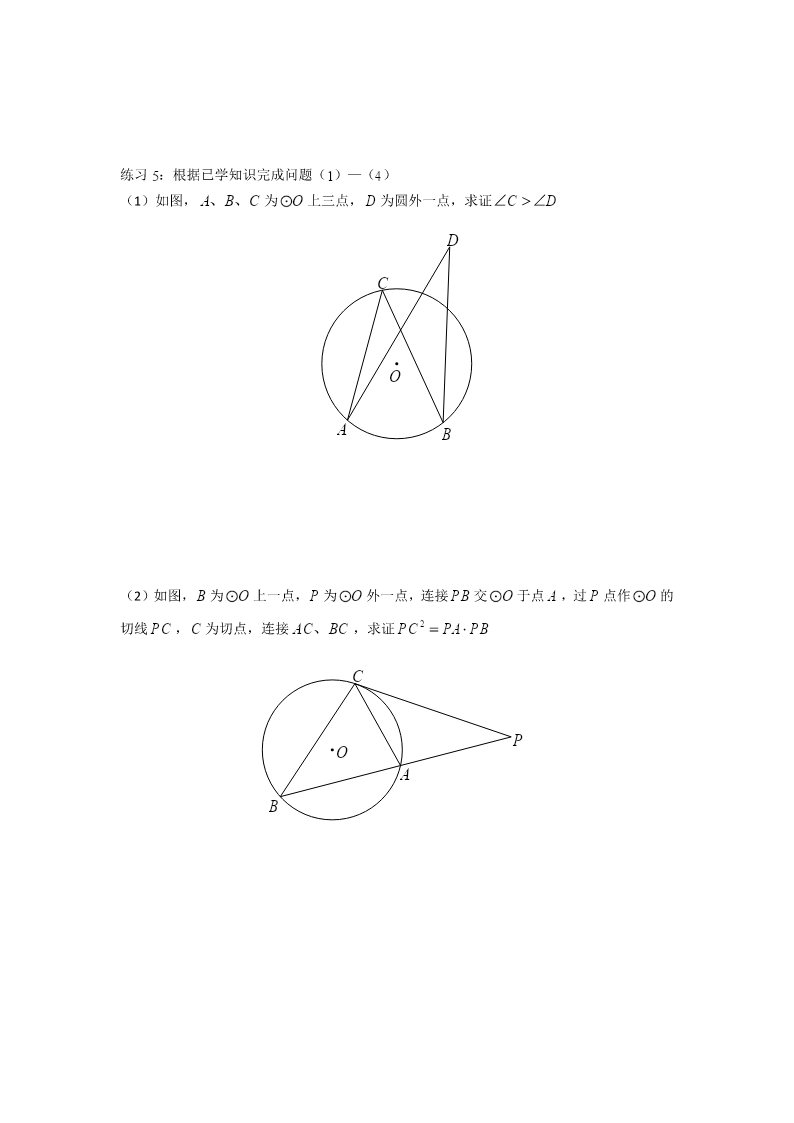

在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

初中数学知识点-53、米勒最值问题.pdf
运用米勒定理简解最大角问题米勒问题和米勒定理1471年,德国数学家米勒向诺德尔教授提出了如下十分有趣的问题:在地球表面的什么部位,一根垂直的悬杆呈现最长?即在什么部位,视角最大?最大视角问题是数学史上100个著名的极值问题中第一个极值问题而引人注目,因为德国数学家米勒曾提出这类问题,因此最大视角问题又称之为“米勒问题”,更一般的米勒问题如下:米勒问题:已知点A、B是MON的边OM上的两个定点,点C是边ON上的动点,则当C在何处时,ACB最大?对米勒问题有如下重要结论我们不妨称之为米勒定理。米勒定理:已

初中数学最值问题集锦+几何的定值与最值.docx
几何的定值与最值几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明.几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有:1.特殊位置与极端位置法;2.几何定理(公理)法;3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考竞赛中,

初中数学最值问题集锦几何的定值与最值.docx
几何的定值与最值学力训练1.如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为,最小值为.2.如图,∠AOB=45°,角内有一点P,PO=10,在角的两边上有两点Q,R(均不同于点O),则△PQR的周长的最小值为.3.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=8,B到MN的距离BD=5,CD=4,P在直线MN上运动,则的最大值等于.4.如图,A点是半圆上一个三等分点,B

初中数学最值问题集锦+几何的定值与最值.docx
几何的定值与最值几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明.几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有:1.特殊位置与极端位置法;2.几何定理(公理)法;3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考竞赛中,

初中数学最值问题集锦几何的定值与最值.docx
几何的定值与最值学力训练1.如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为,最小值为.2.如图,∠AOB=45°,角内有一点P,PO=10,在角的两边上有两点Q,R(均不同于点O),则△PQR的周长的最小值为.3.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=8,B到MN的距离BD=5,CD=4,P在直线MN上运动,则的最大值等于.4.如图,A点是半圆上一个三等分点,B
