
结构向量自回归(SVAR)模型操作步骤ppt课件.ppt

天马****23









亲,该文档总共39页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

结构向量自回归(SVAR)模型操作步骤ppt课件.ppt
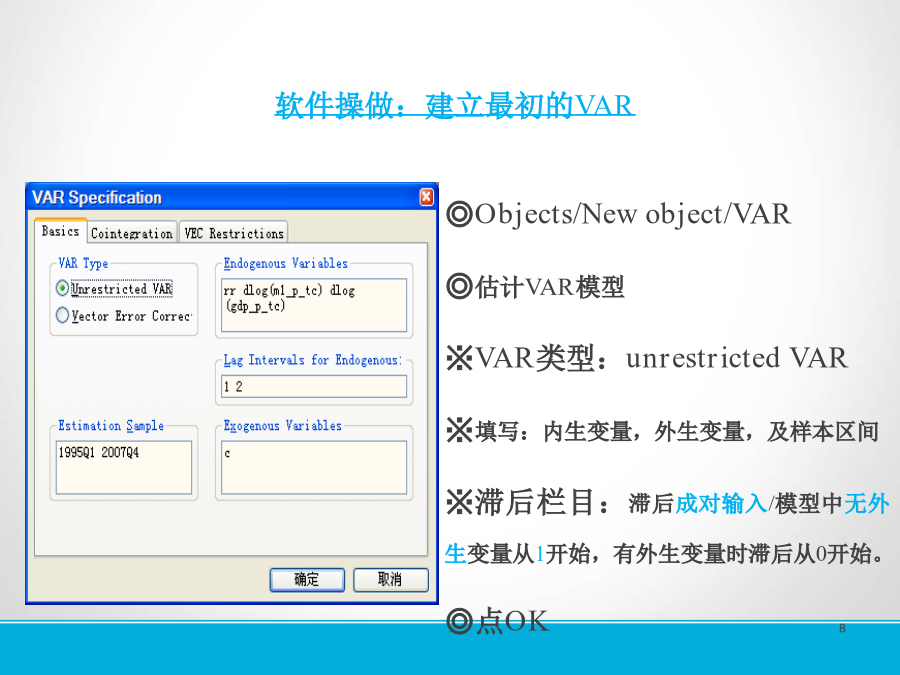
SVAR操作步骤目录注:进行向量自回归与误差修正模型分析首先必须进行稳定性检验各个变量进行稳定性检验结果及分析思路如下:(1)均稳定,则直接进行VAR构建请点VAR/SVAR建模(2)部分稳定,部分不稳定请点VAR/SVAR建模(3)不稳定,但均有相同单整阶数,请点协整检验及VEC(建议做)也可以做VAR建模(建议不做)VAR/SVAR建模第一步初始VAR建模第一步初始VAR建模检验说明对已构建的初始VAR做如:一AR根观察,以便确定模型的稳定性,模型不稳定则某些结果(如脉冲响应函数的标准误差)不是有效的

结构向量自回归SVAR模型操作步骤ppt课件.ppt
SVAR操作步骤目录注:进行向量自回归与误差修正模型分析首先必须进行稳定性检验各个变量进行稳定性检验结果及分析思路如下:(1)均稳定,则直接进行VAR构建请点VAR/SVAR建模(2)部分稳定,部分不稳定请点VAR/SVAR建模(3)不稳定,但均有相同单整阶数,请点协整检验及VEC(建议做)也可以做VAR建模(建议不做)VAR/SVAR建模第一步初始VAR建模第一步初始VAR建模检验说明对已构建的初始VAR做如:一AR根观察,以便确定模型的稳定性,模型不稳定则某些结果(如脉冲响应函数的标准误差)不是有效的

结构向量自回归(SVAR)模型操作步骤.ppt
SVAR操作步骤目录3VAR/SVAR建模第一步初始VAR建模第一步初始VAR建模789最终VAR建模在最终的VAR基础上建立SVAR(可做可不做,建议做)12构建SVAR模型——矩阵约束填写原则(简)构建SVAR模型151617协整检验及VEC协整检验2021222324252627282930313233343536373839

结构向量自回归(SVAR)模型操作步骤.ppt
SVAR操作步骤目录注:进行向量自回归与误差修正模型分析首先必须进行稳定性检验各个变量进行稳定性检验结果及分析思路如下:(1)均稳定,则直接进行VAR构建请点VAR/SVAR建模(2)部分稳定,部分不稳定请点VAR/SVAR建模(3)不稳定,但均有相同单整阶数,请点协整检验及VEC(建议做)也可以做VAR建模(建议不做)VAR/SVAR建模第一步初始VAR建模第一步初始VAR建模检验说明对已构建的初始VAR做如:一AR根观察,以便确定模型的稳定性,模型不稳定则某些结果(如脉冲响应函数的标准误差)不是有效的

VAR-向量自回归模型PPT课件.ppt
向量自回归模型向量自回归(VAR)是基于数据的统计性质建立模型,VAR模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。VAR模型是处理多个相关经济指标的分析与预测最容易操作的模型之一,并且在一定的条件下,多元MA和ARMA模型也可转化成VAR模型,因此近年来VAR模型受到越来越多的经济工作者的重视。VAR(p)模型的数学表达式是(3.1.1)其中:yt是k维内生变量向量,Xt是d维外生变量向量,p是滞后阶数,
