数学建模-线性规划.ppt

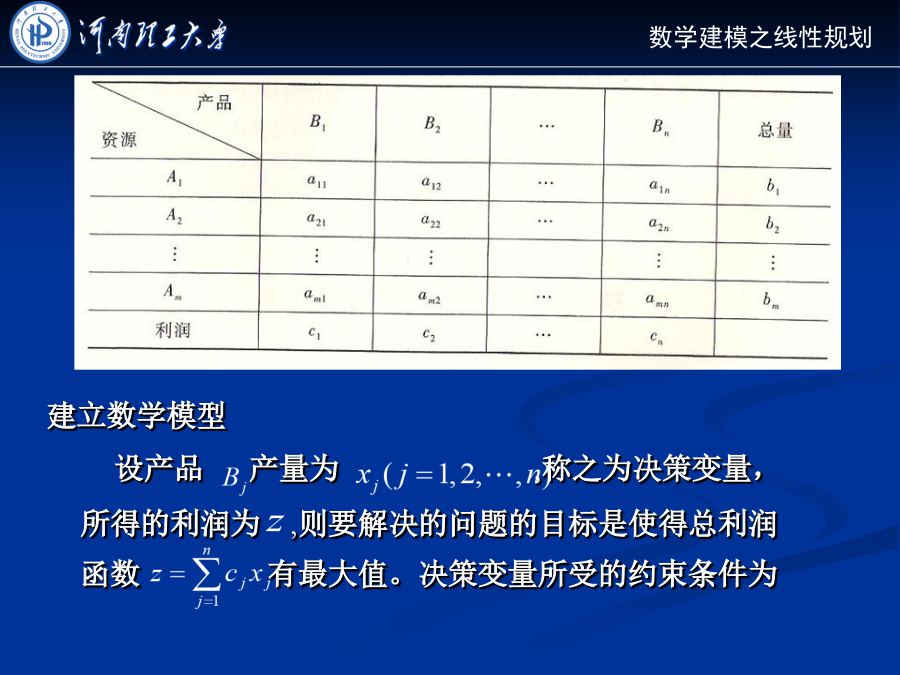
数学建模线性规划方法线性规划问题一个引例建立数学模型
设产品产量为,称之为决策变量，所得的利润为,则要解决的问题的目标是使得总利润函数有最大值。决策变量所受的约束条件为
于是问题归结为求目标函数在约束条件下的最大值问题。显然，目标函数和约束条件分别是关于决策变量的线性函数和线性不等式，即有下面的线性规划模型
目标函数：

约束条件：如果问题的目标函数和约束条件分别是关于决策变量的线性函数和线性不等式，则称该问题为线性规划问题，其模型称为线性规划模型。线性规划模型的一般形式矩阵形式maxcx
s.t.Ax≤b
x≥0线性规划模型的标准形式注：对于非标准型的线性规划模型都可以化为标准型，其方法如下：
（1）目标函数为最大化问题：令,则

（2）约束条件为不等式：对于不等号“≤（≥）”的约束条件，则可在“≤（≥）”的左端加上（或减去）一个非负变量（称为松弛变量）使其变为等式；
（3）对于无约束的决策变量：譬如,则令
,使得,代入模型即可。1、可行解（可行点）
2、可行域
3、最优解线性规划解的几种情形可行域线段组成的凸多边形
目标函数等值线为直线
最优解凸多边形的某个顶点从可行域的某一个顶点开始，只需在有限多个顶点中一个一个找下去，一定能找到最优解。
单纯形算法：从一个顶点转换到另一个顶点，使目标函数下降（上升）最多。Maxz=3x1+x2
s.t.-x1+x2≤2
x1-2x2≤2
3x1+2x2≤14
x1，x2≥0单纯形算法的基本思路单纯形算法举例
-111002
1201010
3100115
-2-30000
①中心部位具有单位子块
②右列元素非负
③底行相应于单位子块的位置的元素为0
在此表的基础上采用单纯形法。
min{2/1,10/2,15/1}=2,选第一行第二列元素1，迭代依次得：
-111002
3^0-2106
40-10113
-5*03006

011/31/304
10-2/31/302
005/3^-4/315
00-1/3*5/3016

0103/5-1/53
100-1/52/54
001-4/53/53
0007/51/517

初始基可行解的确定
如果线性规划问题为标准型（即约束方程全为等式），则从系数矩阵中观察一般可以得到一个阶单
位矩阵，如果所有约束条件是形如“≤”的不等式，则引入
个松弛变量，可化为标准型，并将变量重新排序编号，即可得到一个阶单位矩阵；如果问题的约束条件的不
等号为“≥”和“＝”，则首先引入松弛变量化为标准型，再通
过人工变量法总能得到一个阶单位矩阵，综上所述，取如上阶单位矩阵为初始可行基，即；将相应的约束方程组变为
线性规划的对偶问题对B企业，希望花最小的代价将A的所有资源及生产权收买过来，即问题为

或

这也是一个线性规划问题，该问题称为问题例1的对偶问题；例1称为此对偶问题的原问题，即两者为相互对偶的问题。对偶问题中的对偶变量另一个重要意义就是“影子价格”。原问题与对偶问题的关系

设线性规划的原问题为，相应
的对偶问题为，则有如下性质：
（1）对偶问题的对偶问题为原问题；
（2）如果原问题（对偶问题）为无界解，则其对偶问题（原
问题）无可行解，反之不然；
（3）设是原问题的可行解，是对偶问题的可行解，
且，则和分别是原问题和对偶问题的
最优解；
（4）如果原问题有最优解，则其对偶问题也必有最优解，且
有根据对偶问题的性质和原问题与对偶问题的解之间的关系，原问题的检验数是对偶问题的基解，求解中通过若干步的迭代后，当原问题检验数为对偶问题的基可行解时，则也就得到了原问题和对偶问题的最优解，迭代中主要是根据检验数的符号判断是否得到了最优解。在线性规划模型中，总
是假设都是常数向量，但实际中这些数值许多
是由试验或测量得到的试验值和预测值，特别是在迭
代计算中也都是近似值。一般A表示工艺条件,b表示
资源条件,c表示市场条件，实际中多种原因都可能
引起它们的变化。
线性规划的灵敏度分析用lingo软件求解LP问题LINGO的语法规定：
（1）求目标函数的最大值或最小值分别用MAX=…或MIN=…来表示；
（2）每个语句必须以分号“；”结束，每行可以有许多语句，语句可以跨行；
（3）变量名称必须以字母(A~Z)开头，由字母、数字(0~9)和下划线所组成，长度不超过32个字符，不区分大小写；
（4）可以给语句加上标号，例如[OBJ]MAX=200*X1+300*X2；
（5）以惊叹号“！”开头，以分号“；”结束的语句是注释语句;
（6）如果对变量的取值范围没有作特殊说明，则默认所有决策变量都非负；
（7）LINGO模型以语句“MODEL：”开头，以“END”结束，对于比较简单的模型，这两个语句可以省略。例2(运输问题)两个粮库A1,A2,向三个粮站B1,B