最短路径Dijkstra算法.pptx

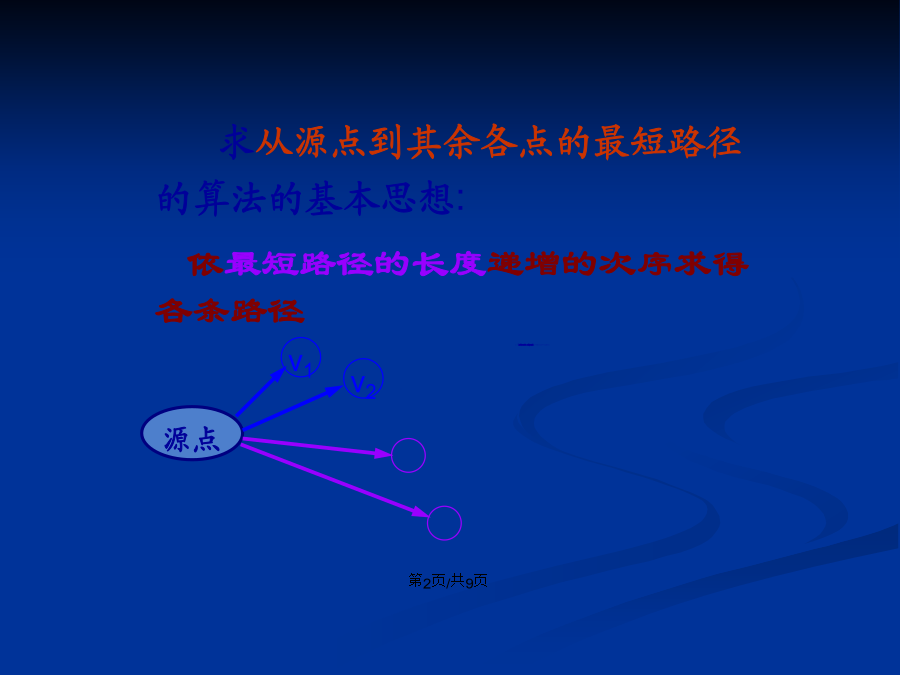
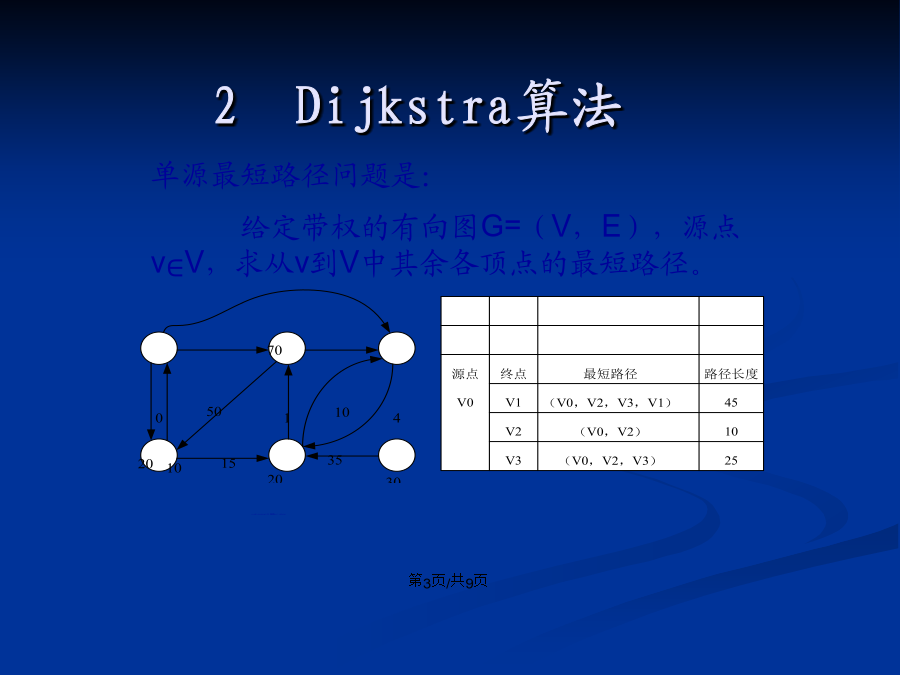
会计学1最短路径求从源点到其余各点的最短路径的算法的基本思想:2Dijkstra算法即迪杰斯特拉算法，其基本思想如下：3）每次从集合V-S中取出具有最短特殊路径长度的顶点u，将u加到S中，同时对数组Dist做必要的修改。若Dist[u]+[u][k]<Dist[k]
则将Dist[k]改为Dist[u]+[u][k]。
其中，特殊路径指从源点到u中间只经过S中顶点的路径。 若带权图G如下所示，根据上述算法来求解源点v0到v2的最短路径。根据以上分析和举例，不难得出狄杰斯特拉算法，其描述如下：D[v0]=0;final[v0]=TRUE;//初始化，v0顶点在S集中
//开始主循环，每次求得v0到某个顶点v的最短距离，将v加到S集
for(i=1;i<G.vexnum;i++){
min=INFINITY;
for(w=0;w<G.vexnum;i++)//求得当前离v0顶点最近距离
if(!final[w])
if(D[w]<min){v=w;min=D[w];}
final[v]=TRUE;//离v0最近距离顶点v加入S集
for(w=0;w<G.vexnum;w++)//更新当前最短路径及距离
if(!final[w]&&(min+G.arcs[v][w]<D[w])){
D[w]=min+G.arcs[v][w];
P[w]=P[v];P[w][w]=TRUE;}
}
}