通信原理(7).ppt

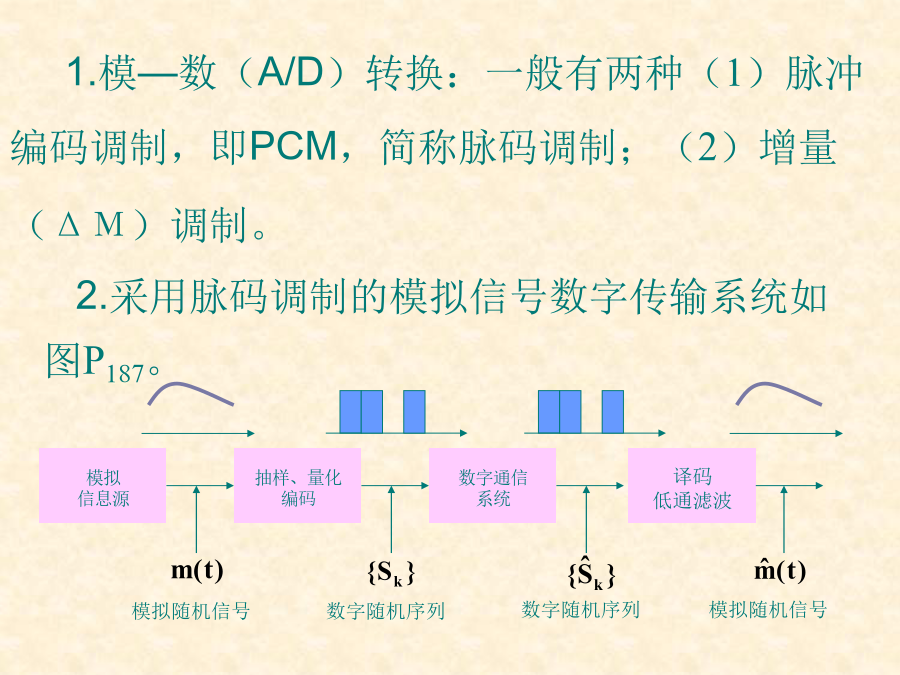
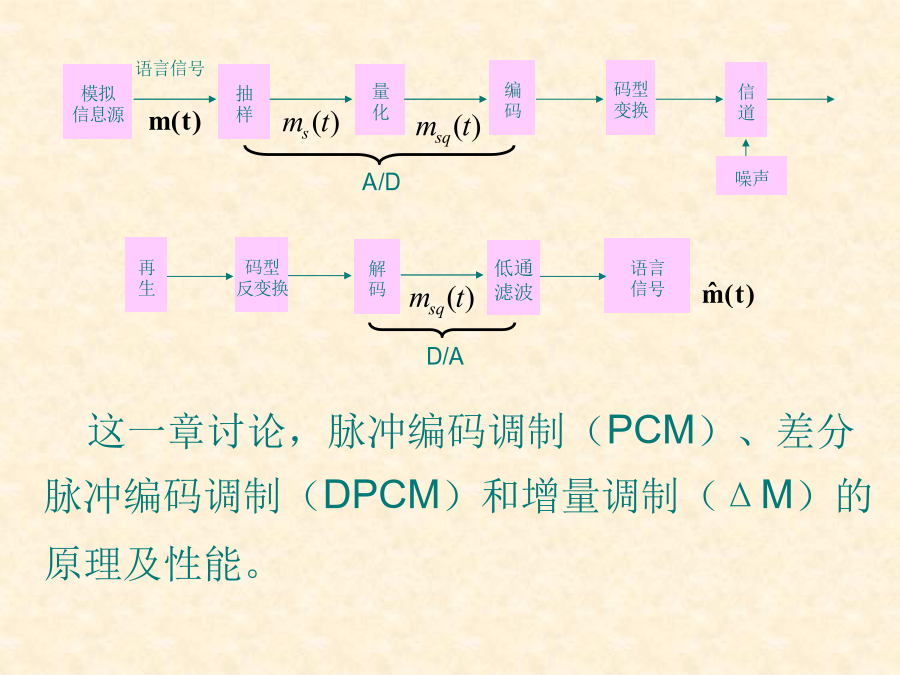
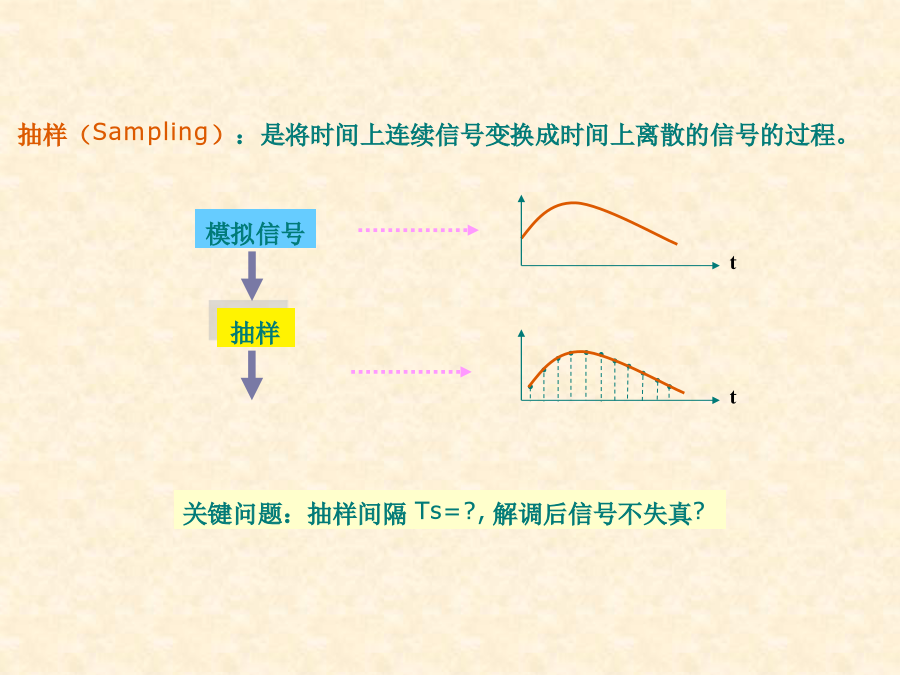
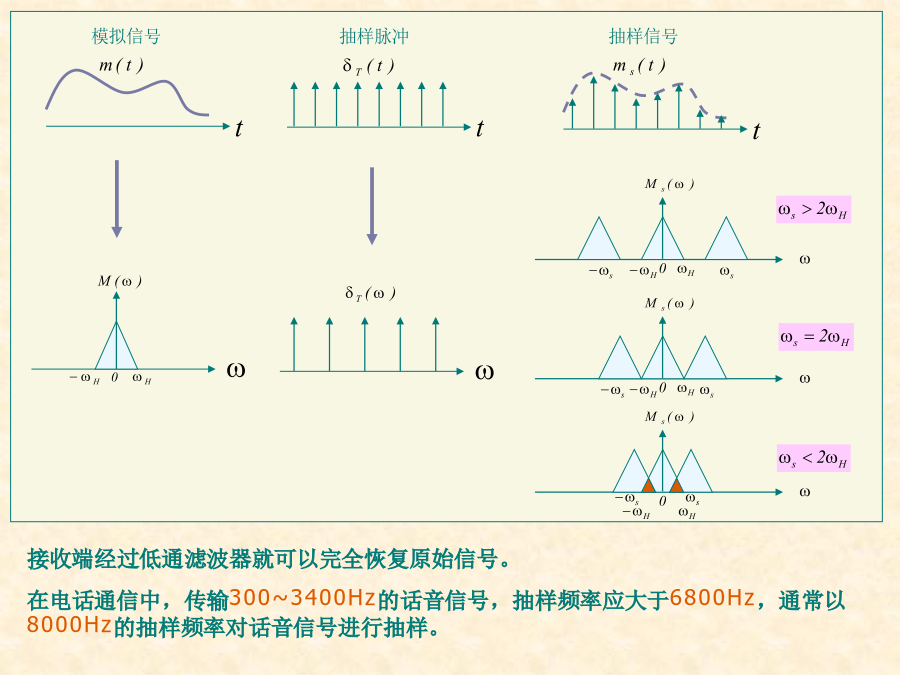
第7章模拟信号的数字传输7.1引言1.模—数（A/D）转换：一般有两种（1）脉冲
编码调制，即PCM，简称脉码调制；（2）增量
（ΔΜ）调制。
2.采用脉码调制的模拟信号数字传输系统如图P187。模拟
信息源抽样定理可知，对连续信号（模拟信号）时
间上进行抽样，速率达到一定。这些抽样值就能
准确地确定原信号，抽样定理对模拟信号的数字
传输奠定了理论基础。如果以秒的间隔对它进行等间隔抽样，则
可m(t)将被所得到的抽样值完全确定。
此定理称为均匀抽样定理，均匀间隔
秒上给定信号的抽样值来表征信号。这意味着
，若m(t)的频谱在某一角频率ωH以上为零，则
m(t)中的全部信息完全包含在其间隔不大于1/2
fH秒的均匀抽样序列里。换句话说，在信号最高
频率分量的每一个周期内起码应抽样两次。抽样（2）假定信号m(t)，周期性冲激函数，则该式表明，已抽样信号的频谱是无穷多
个间隔为相叠加而成。这就意味着
中包含的全部信息。P189上有图解分析图7-3.模拟信号需要注意，若抽样间隔T变得大于1/2fH，则
的卷积在相邻的周期内存在重叠（亦称混叠），因此不能由恢复。可见是抽样的最大间隔，称为奈奎斯特间隔。使已抽样信号通过低通滤波器使得出信号
此滤波器图7-2（b），截止频率为，增益为
故其传输函数可以表示为：将时间卷积定理用于式（7.2-6）得即将每个抽样值和一个抽样函数相乘后得到的所
有波加起来便是。如图（7--3）（g）所示。
需要指出，以上讨论是限于频带有限的信号，严
格来说，频带有限的信号并不存在，但实用的意
义上说，所有信号频谱密度函数在较高频率上都
要减小，大部分能量由一定频率范围内的分量所
携带。这种信号认为有限的。以上分析是低频之间，而信号限制在
（信号的最低频率）与（信号的最低高频率）之间，
带通型连续信号。前面的抽样脉冲是周期性冲激函数。这是一种理想的
情况，称为理想抽样。实际中采用脉冲宽度τ相对于抽样
周期Ts窄得多的脉冲序列s(t)近似代替冲激序列,它的已抽
样信号分为自然抽样和平顶抽样。1.脉冲调制脉宽调制(PDM)和脉位调制(PPM)等。我们主要学习脉幅调制。因为它是脉冲编码调制的基础。脉冲调制是用离散脉冲串做为载波的调制方式。所谓脉冲振幅调制，即是脉冲载波的幅度随基带信号变化的调制方式，如果脉冲载波是由冲激脉冲组成的。则前面所说的抽样定理，就是脉冲振幅调制的原理，冲激脉冲串不能实现，通常窄脉冲串来实现。P194有波形。图中s(t)是载波。可见，平顶抽样后各分量有频率失真。信号是m(t)与s(t)的乘积，所以,已抽样信号波形及频谱可求得(抽样脉冲为矩形窄脉冲)。（3）瞬时抽样。利用式（7.2-5）的结果，上式变成为了从已抽样信号中恢复原基带信号m(t)，可以用图7-10所示的原理方框图恢复原始信号。从式（7.3-2）看出，不能直接使用低通滤波器滤除所需的信号，是因为M(ω)受到了H(ω)的加权。如果我们在接收端低通滤波器之前用特性为1/H(ω)的网络加以修正，则低通滤波器输入信号的频谱变成为模拟信号数字化的第二步是幅值上的离散化，即量化，把抽样值m(kT)用N个二进制数字信号表示该值的大小，那么N个二进制信号能个电平样值相对应，而不能用无穷多个电平值相对应。抽样值被划分成M个离散电平，此电平被称作为量化电平。这样才能够利用数字传输系统来实现抽样值信息的传输。7.4.1均匀量化量化器量化器输出为4.信号功率与量化噪声功率之比书上P197有例题7.4.1看看7.4.2非均匀量化1.律压缩特性（美国）分析压缩后量化信噪比改善的程度x10.3160.10.03120.010.0032.A律压缩特性（欧洲、中国）斜率图中,把x轴的0~1分为8个不均匀段,其方法是:将0~1之间
，一分为二,其中点为,~1之间作为第8段;剩余的0~
再一分为二，中点为，取~之间作为第7段；这样由8段构成的一条折线。该折线与式（7.4-13a）及式（7.4-13b）表示的压缩特性近似了。该8段的斜率为得P203表7-2。第1段斜率，第2段斜率表7-313折线分段时的x值与计算的x值比较表13折线4.律压缩特性的15折线近似2.PCM调制实例编码（Encoding）：将模拟信号的抽样量化值变换成二进制代码。7.5.1脉冲编码调制原理2.编码原理②折叠二进码折叠二进码除了最高位外，其上半部分与下半部分的码型呈倒影关系—折叠关系.最高位是它表示正负信号，极性码。见表。C1C2C3C4C5C6C7C8量化电平
编号非均匀量化与均匀量化作一比较。假设以非均匀量化时的最小量化间隔（第1、2段落的量化间隔）作为均匀量化时的量化间隔，那么从13折线的第一段到第八段所包含的均匀量化数分别为16、16、32、64、128、256、512、1024，总共有204