基于Matlab系统辨识工具箱的参数辨识.pdf

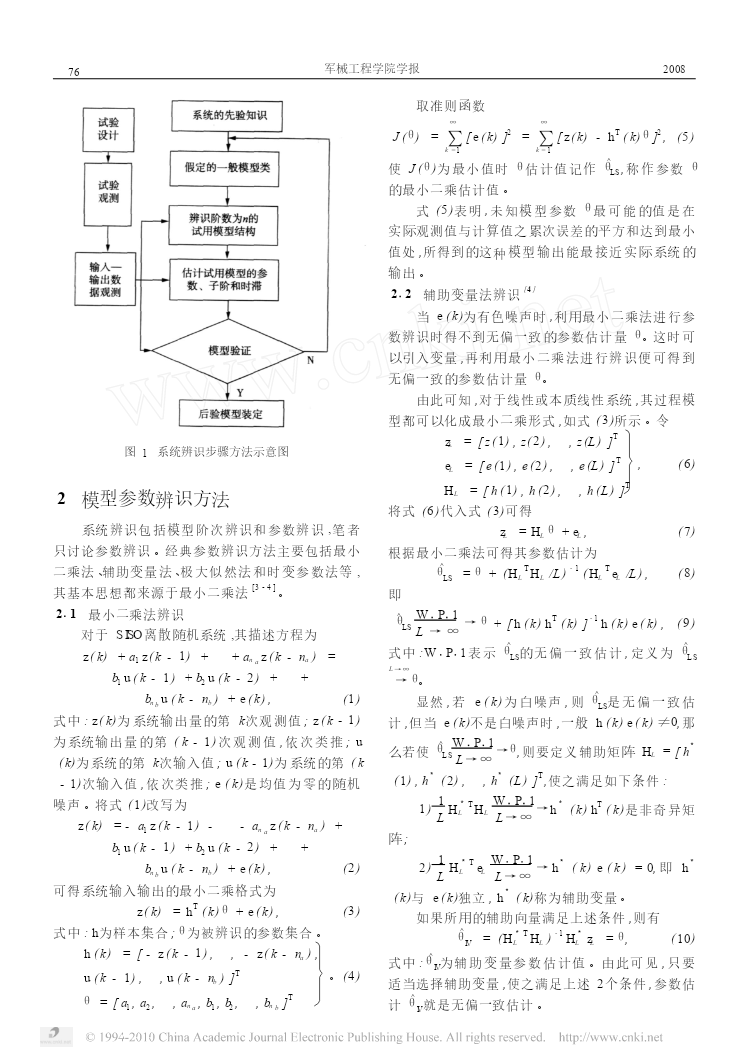
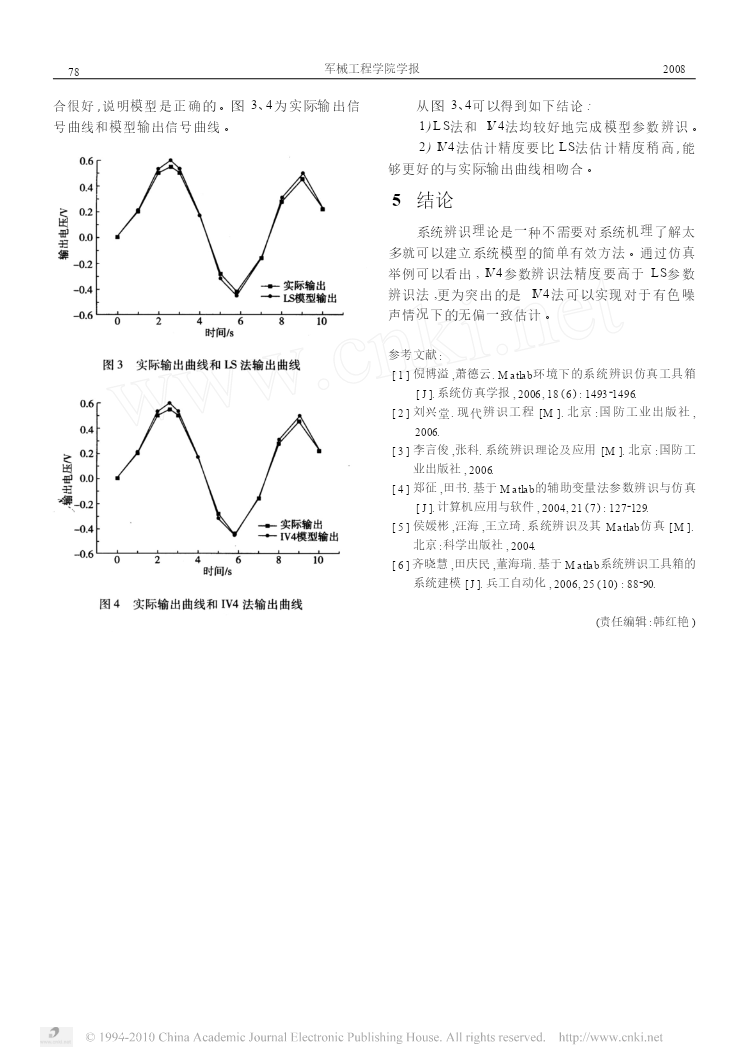
第20卷第4期军械工程学院学报Vol120No14
2008年8月JournalofOrdnanceEngineeringCollegeAug.,2008

文章编号:1008-2956(2008)04-0075-04

基于Matlab系统辨识工具箱的参数辨识

王向东1,魏明1,赵建文2,陈翔1
(1.军械工程学院弹药工程系,河北石家庄050003;2.辽阳地区军代室,辽宁辽阳111000)

摘要:论述了系统辨识的基本理论,针对最小二乘法参数辨识的缺陷引入了辅助变量法参数辨识。根据Matlab
系统辨识工具箱中的一些基本函数,结合实例对最小二乘法参数辨识和辅助变量法参数辨识进行了对比分析,
结果表明基于辅助变量法模型的输出与原系统输出相吻合。
关键词:Matlab;参数辨识;最小二乘法;辅助变量法
中图分类号:TP273文献标识码:A

ParameterIdentificationBasedonSystemIdentification
ToolboxinMatlab

WANGXiang2dong1,WEIMing1,ZHAOJian2wen2,CHENXiang1
(1.DepartmentofAmmunitionEngineering,OrdnanceEngineeringCollege,Shijiazhuang050003,China;
2.MilitaryRepresentativesOfficeinLiaoyang,Liaoyang111000,China)

Abstract:Thisarticleintroducesthebasictheoryofsystemidentification.Thenaccordingtothedefectof
theleastsquaremethod,itintroducestheprincipleofsupplementaryvariableinparameteridentification.
ThispaperalsolistssomebasicparameteridentificationfunctionsinMatlabsystemidentificationtoolbox.
Finally,thepapercontraststhetwoparameteridentificationmethodsthroughoneexample.Theexample
showsthatthesupplementaryvariablemethodsuitstheoriginallysystem’soutputdatabetter.
Keywords:Matlab;parameteridentification;theleastsquaremethod;supplementaryvariablemethod

在实际工程领域存在着大量的对象,为了研究1)L1A1Zadeh定义:辨识是在输入输出数据的
其行为特性需要建立其数学模型。按照建模时对系基础上,从给定的模型类中,确定与系统等价的模
统先验知识了解多少,可以将模型分为3类:白箱模型。
型、灰箱模型和黑箱模型。系统辨识理论是在先验2)P1Eykhoff定义:辨识问题可以归结为用某个
知识不完备的情况下,根据系统的输入输出数据提模型来辨识客观系统(或将要构造的系统)本质特
取模型信息,从而构建系统模型,属于黑箱模型[1]。征的演算,并用这个模型把对客观系统的理解表示
随着计算机技术的发展,出现了一些计算机辅成有用的形式。
助辨识软件。笔者研究了如何利用Matlab系统辨3)L1Ljung定义:辨识有3个要素———数据、模
识工具箱对系统进行模型参数辨识,并运用最小二型类和准则。辨识就是按照某个准则在模型类中选
乘法(LS)及辅助变量法(IV)对模型参数进行辨识。择与数据拟合最好的模型。
从上面的定义可以看出,辨识就是利用所观测
1系统辨识基本理论
到的系统输入输出数据(往往含有噪声),根据所选
很多学者都曾给辨识下过定义,下面介绍几个择的原则,从模型类中确定与所测系统拟合的最好
比较典型适用的定义[2-3]。的模型。
系统辨识的方法和步骤如图所示。
收稿日期:2008204230;修回日期:20082062151
作者简介:王向东(1984—),男,硕士研究生.
76军械工程学院学报2008

取准则函数
∞∞
J(θ)=∑[e(k)]2=∑[z(k)-hT(k)θ]2,(5)
k=1k=1
^
使J(θ)为最小值时θ估计值记作θLS,称作参数θ
的最小二乘估计值。
式(5)表明,未知模型参数θ最可能的值是在
实际观测值与计算值之累次误差的平方和达到最小
值处,所得到的这种模型输出能最接近实际系统的
输出。
212辅助变量法辨识[