一种基于距离函数定义边界的二维有限元网格剖分算法.pdf

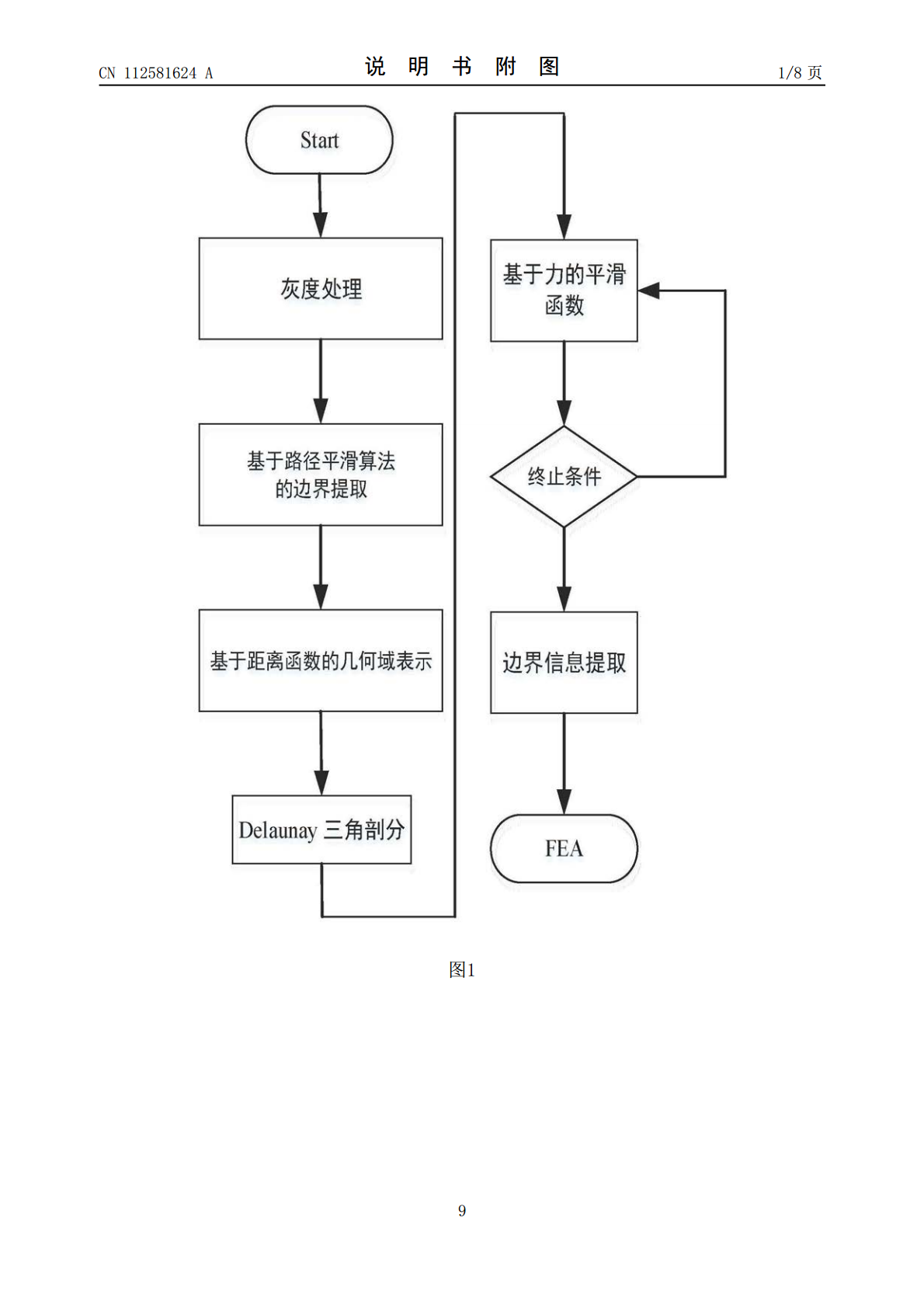
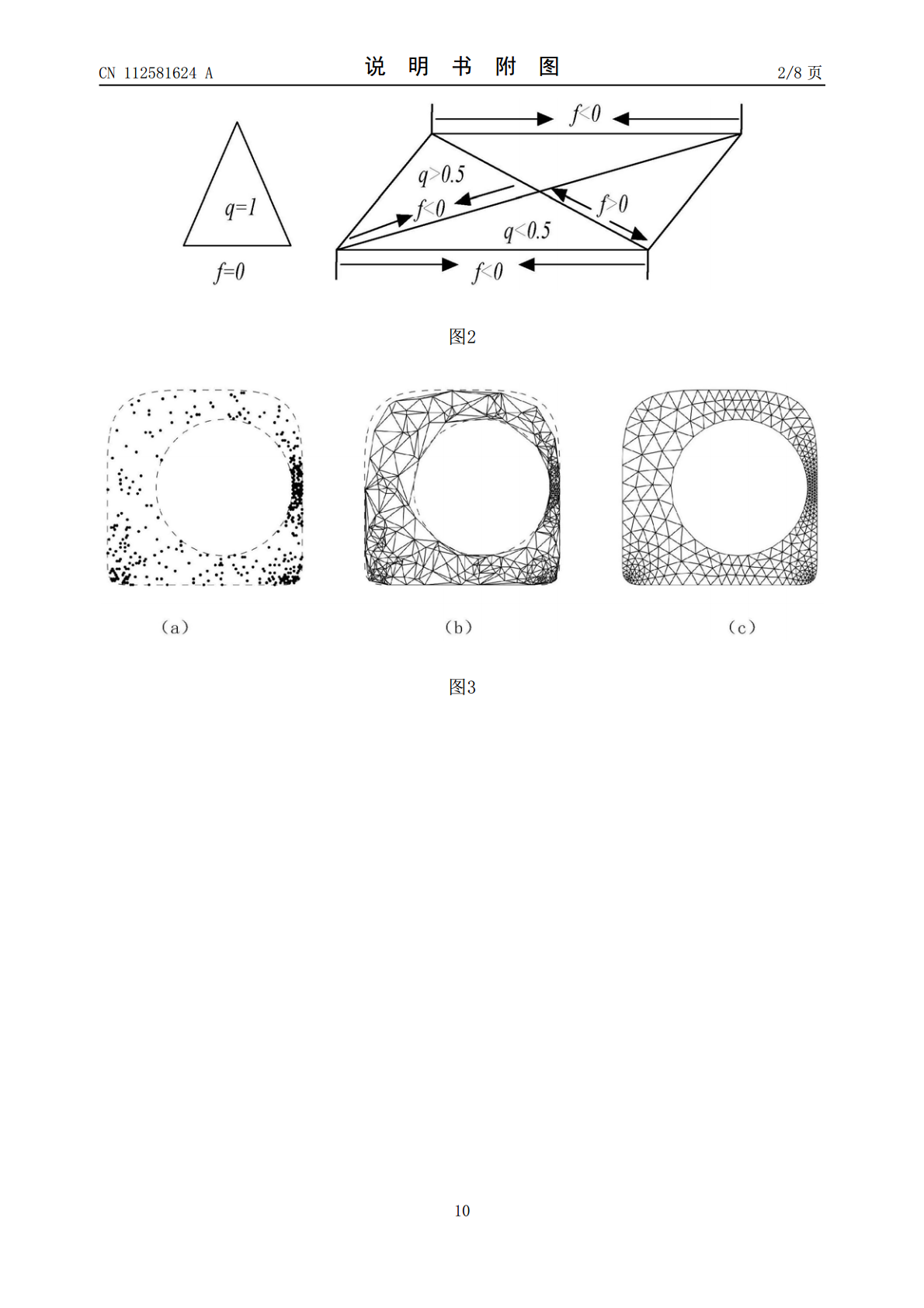
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN112581624A(43)申请公布日2021.03.30(21)申请号202011538435.3(22)申请日2020.12.23(71)申请人中国计量大学地址310018浙江省杭州市下沙高教园区学源街258号(72)发明人章春锋汪伟安斯光林德辉(74)专利代理机构浙江专橙律师事务所33313代理人朱孔妙(51)Int.Cl.G06T17/20(2006.01)权利要求书1页说明书6页附图8页(54)发明名称一种基于距离函数定义边界的二维有限元网格剖分算法(57)摘要本发明涉及电磁场有限元数值分析领域，特别是涉及一种基于距离函数定义边界的二维有限元网格剖分算法。包括：距离函数构造步骤，主要分为两种情况，规则性形状通过几何函数来表示，非规则形状通过图像处理方式来抽象出边界轮廓，并通过基于路径优化的边界平滑算法对边界进行平滑处理。Delaunay三角剖分步骤，用Delaunay三角剖分确定桁架的拓扑，以备网格平滑步骤所用；加入质量评估函数，对网格迭代次数进行限制。网格平滑步骤，通过基于力的网格平滑算法，对网格质量以及效率进行提升。后处理模块，基于距离函数以及二阶高斯投影方法进行不同媒质边界的筛选，根据不同应用场景给予不同边界激励条件，进而求解得到结果。CN112581624ACN112581624A权利要求书1/1页1.一种基于距离函数定义边界的二维有限元网格剖分算法，其特征在于：包括如下步骤：步骤1：构建距离函数，并初始化，在边界框中生成等距点的网格，给定为节点坐标x和y，坐标存储在2列的数组中；步骤2：调用距离函数，并将节点位置作为输入，输出结果是从节点到几何边界的距离的列向量，仅保留负距离的内部点，然后，在每个节点上评估h(x,y)并以与1/h(x,y)2成正比的概率拒绝点，用户的固定节点数组位于数组中的第一行，还要对节点进行去重；步骤3：二维有限元网格剖分算法进入主循环，在该循环中，节点位置得到了迭代改进，开始循环；步骤4：执行Delaunay三角剖分并移除质心在外部的三角形，逆时针重新排列三角形顶点，形成所有边且无重复并提取边界边；步骤5：基于力的平滑函数：在应用力平衡平滑函数之前，先用Delaunay三角剖分确定桁架的拓扑，通常，对于数组以及每次点移动都进行此操作，以保持正确的拓扑；为了节省计算时间，当自上一次三角剖分以来的最大位移大于ttol时，需重新三角剖分；计算和组合边缘力并移动节点，经过N次迭代后，归一化长度大于1.5的边需通过添加中点进行分割，Delaunay函数生成点集的凸包的三角剖分，并且必须删除几何图形外部的三角形，在此，如果三角形的质心的d＞0，则该三角形将被删除；三角形列表是具有3列的数组，每行用三个整数索引代表一个三角形，在创建边列表时，每个三角形贡献三个节点对，由于大多数配对将出现两次，必须删除重复项，将网格的边界节点确定为边界边缘的端点，如果点在更新数组之后结束于几何图形之外，则将其移回到边界上最近的点；步骤6：终止条件：计算内部点的相对位移，如果在当前的迭代中检测到大位移，转到步骤5；同时通过计算三角形面积检查三角形质量，如果三角形元素质量均大于0.5，确认终止；步骤7：基于距离函数以及二阶高斯投影方法进行不同媒质边界的筛选，根据不同应用场景给予不同边界激励条件；步骤8：进行FEA。2.根据权利要求1所述的一种基于距离函数定义边界的二维有限元网格剖分算法，其特征在于：几何域的定义，需由闭合的距离函数来表示边界。3.根据权利要求1所述的一种基于距离函数定义边界的二维有限元网格剖分算法，其特征在于：在应用基于力平衡的平滑函数之前，先用Delaunay三角剖分确定桁架的拓扑；再进行基于力的平滑函数过程中，每个网格单元的质量将作为力平滑函数进行自适应的凭据。2CN112581624A说明书1/6页一种基于距离函数定义边界的二维有限元网格剖分算法技术领域[0001]本发明涉及电磁场有限元数值分析领域，特别是涉及一种基于距离函数定义边界的二维有限元网格剖分算法。背景技术[0002]优异的适应场域边界几何形状以及媒介物理性质变异的能力，使有限元法成为各类电磁场、电磁波工程问题定量分析和优化设计的主导数值计算方法之一。一般而言，有限元分析划分为：建立模型(前处理)、计算求解、结果处理和评定(后处理)。其中，各阶段所用的时间占比分别为：40％‑60％、5％‑10％、30％‑50％。因而，如何将实际工程中复杂场域离散为“有限单元”，这一剖分问题在数值分析过程是极其关键的一步，直接决定了最终结果的准确性和有效性。[0003]网格生成器诸如大型商业软件CAE/Maxwell，以映射法为理论基础。其主要思想是，通过合适的映射函数将待剖分