
一元线性回归模型的统计检验.ppt

天马****23









亲,该文档总共19页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

一元线性回归模型的统计检验.ppt
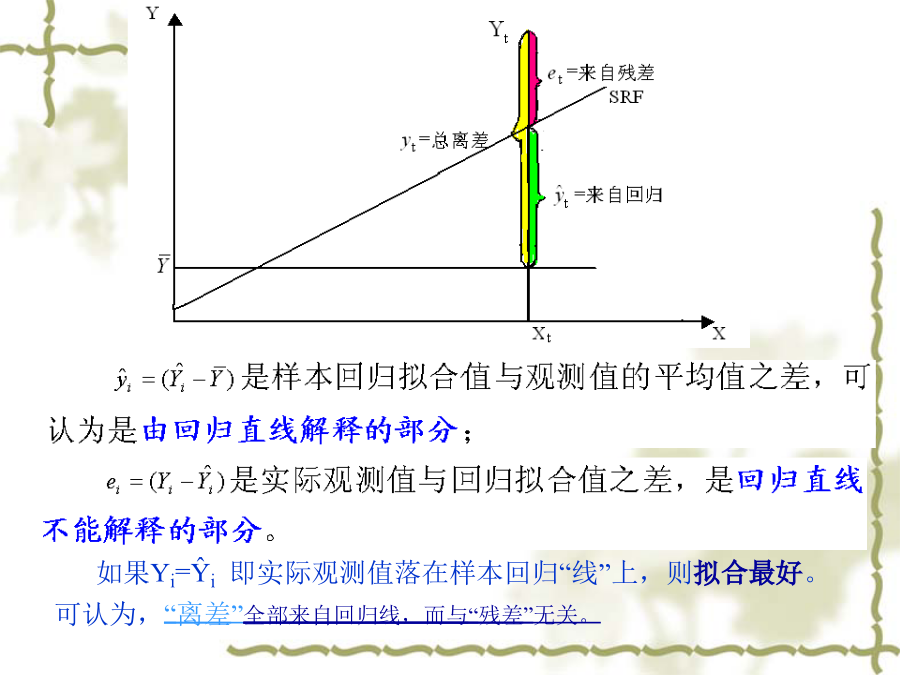
回归分析是要通过样本所估计的参数来代替总体的真实参数,或者说是用样本回归线代替总体回归线。一、拟合优度检验1、总离差平方和的分解如果Yi=Ŷi即实际观测值落在样本回归“线”上,则拟合最好。可认为,“离差”全部来自回归线,而与“残差”无关。对于所有样本点,则需考虑这些点与样本均值离差的平方和,可以证明:TSS=ESS+RSS2、可决系数R2统计量二、变量的显著性检验1、假设检验2、变量的显著性检验检验步骤:对于一元线性回归方程中的0,可构造如下t统计量进行显著性检验:t统计量的计算结果分别为:假设检验可以

一元线性回归模型的统计检验.ppt
回归分析是要通过样本所估计的参数来代替总体的真实参数,或者说是用样本回归线代替总体回归线。一、拟合优度检验1、总离差平方和的分解如果Yi=Ŷi即实际观测值落在样本回归“线”上,则拟合最好。可认为,“离差”全部来自回归线,而与“残差”无关。对于所有样本点,则需考虑这些点与样本均值离差的平方和,可以证明:TSS=ESS+RSS2、可决系数R2统计量二、变量的显著性检验1、假设检验2、变量的显著性检验检验步骤:对于一元线性回归方程中的0,可构造如下t统计量进行显著性检验:t统计量的计算结果分别为:假设检验可以

一元线性回归模型的统计检验PPT.ppt
一元线性回归模型的统计检验(优选)第二节一元线性回归模型的统计检验总变差的分解拟合优度(可决系数)▼如果或者则拒绝原假设,而接受备择假设定义:回归平方和(解释了的变差ESS)在总变拟合优度(可决系数)或(优选)第二节一元线性回归模型的统计检验与相对应分析Y的观测值、估计值与平均值的关系这样计算的是Y的一个点估计值▼如果或者则拒绝原假设,而接受备择假设▼如果或者则拒绝原假设,而接受备择假设或拟合优度(可决系数)将上式两边平方加总,可证得P值检验是比较和pP▼如果或者则拒绝原假设,而接受备择假设或将上式两边平

§2.3一元线性回归模型的统计检验.pptx
§2.3一元线性回归模型的统计检验回归分析是要通过样本所估计的参数来代替总体的真实参数,或者说是用样本回归线代替总体回归线。一、拟合优度检验如果Yi=Ŷi即实际观测值落在样本回归“线”上,则拟合最好。可认为,“离差”全部来自回归线,而与“残差”无关。TSS=ESS+RSS1、假设检验检验步骤:t统计量的计算结果分别为:于是得到:(1-)的置信度下,i的置信区间是1、总离差平方和的分解对于所有样本点,则需考虑这些点与样本均值离差的平方和,可以证明:2、可决系数R2统计量二、变量的显著性检验2、变量的显著

§24多元线性回归模型的统计检验.ppt
§2.4多元线性回归模型的统计检验StatisticalTestofMultipleLinearRegressionModel我们所要进行的统计检验包括两个方面,一方面检验回归方程对样本数据的拟合程度,通过可决系数来分析;另一方面检验回归方程的显著性,通过假设检验对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断,包括对回归方程线性关系的检验和对回归系数显著性的检验。一、拟合优度检验TestingtheSimulationLevel1、总体平方和、残差平方和和回归平方和2、拟合优度检验
