
二分图匹配—匈牙利算法构图最大流.ppt

天马****23









亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

二分图匹配—匈牙利算法构图最大流.ppt
基本概念最大匹配匈牙利算法匈牙利算法匈牙利算法bool寻找从k出发的对应项出的可增广路{while(从邻接表中列举k能关联到顶点j){if(j不在增广路上){把j加入增广路;if(j是未盖点或者从j的对应项出发有可增广路){修改j的对应项为k;则从k的对应项出有可增广路,返回true;}}}则从k的对应项出没有可增广路,返回false;}匈牙利算法模板(详见POJ2239)intmain(){inti,j,p,q,t;while(scanf("%d",&n)!=EOF){memset(map,0,size

ACM讲课之二分图匹配(匈牙利算法)-PPT.ppt
ACM讲课之二分图匹配(匈牙利算法)什么是二分图?什么是二分图匹配?二分图的最大匹配匈牙利算法必备知识:1.盖点:有被M中的边关联到的节点,未盖点则相反。2.增广路径:若二分图中有一条路径p,其起始点和结束点都是未盖点,其间属于M的边和不属于M的边交替出现,则称路径p是一条关于M的增广路径。匈牙利算法:计算二分图最大匹配就是应用增广路径的概念,每次寻找一条关于M的增广路径p,通过M和增广路径进行异或,使得M中的匹配数增加1。以此类推,直至二分图中不存在关于M的增广路径为止。此时得到匹配M就是图G的一个最大

齐鲁医学二分图匹配基于匈牙利算法和KM算法.docx
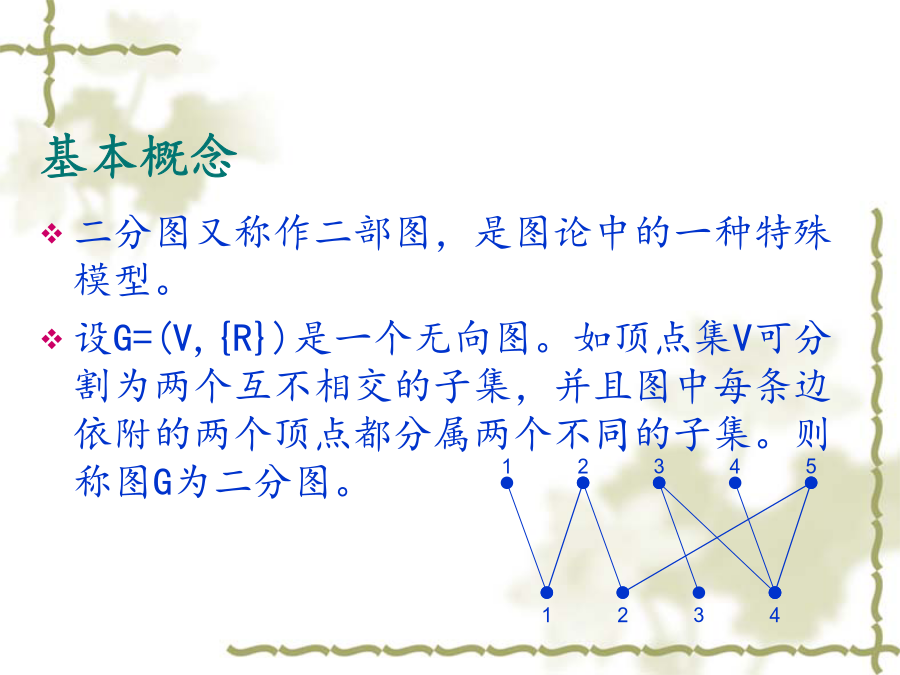
精品医学文档齐鲁医学二分图匹配基于匈牙利算法和KM算法-1--3-精品医学文档二分图匹配----基于匈牙利算法和KM算法2022-05-1916:54设G=(V{R})是一个无向图。如顶点集V可分割为两个互不相交的子集并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。v给定一个二分图G在G的一个子图M中M的边集{E}中的随意两条边都不依附于同一个顶点则称M是一个匹配。v选择这样的边数最大的子集称为图的最大匹配问题(maximalmatchingproblem)v如果一个匹

【精编医学资料】二分图匹配基于匈牙利算法和KM算法.docx
二分图匹配----基于匈牙利算法和KM算法2007-09-1916:54设G=(V{R})是一个无向图。如顶点集V可分割为两个互不相交的子集并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。v给定一个二分图G在G的一个子图M中M的边集{E}中的任意两条边都不依附于同一个顶点则称M是一个匹配。v选择这样的边数最大的子集称为图的最大匹配问题(maximalmatchingproblem)v如果一个匹配中图中的每个顶点都和图中某条边相关联则称此匹配

最新精编医学专题—二分图匹配基于匈牙利算法和KM算法.docx
二分图匹配----基于匈牙利算法和KM算法2007-09-1916:54设G=(V{R})是一个无向图。如顶点集V可分割为两个互不相交的子集并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。v给定一个二分图G在G的一个子图M中M的边集{E}中的任意两条边都不依附于同一个顶点则称M是一个匹配。v选择这样的边数最大的子集称为图的最大匹配问题(maximalmatchingproblem)v如果一个匹配中图中的每个顶点都和图中某条边相关联则称此匹配
