预览加载中，请您耐心等待几秒...

常用的坐标变换.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共18页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

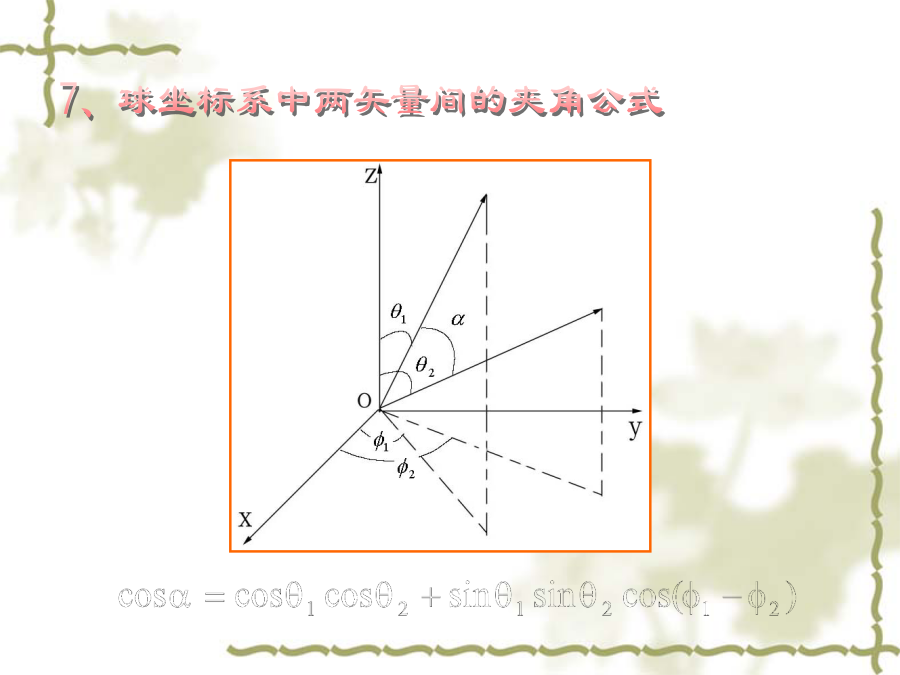
2、圆柱坐标系与笛卡儿坐标系中矢量坐标变换3、圆柱坐标系单位矢量的偏导数4、笛卡儿坐标系与球坐标系的变换5、球坐标系与笛卡儿坐标系中矢量的坐标变换7、球坐标系中两矢量间的夹角公式定义：设闭合曲面S包围着体积V，穿过S的矢量场的通量与V之比，在V0时的极限称为矢量场的散度。定义：在矢量场的某点上定义一个矢量，其方向为该点有最大环量面密度的方向，其大小等于这个最大环量面密度的值，这个矢量叫做该点的旋度。定义：标量场中的某点上定义一个矢量，其方向为函数在该点变化率最大的方向，其大小等于这个最大变化率的值，这个矢量叫做函数在该点的梯度。 函数在该点附近沿l方向的增量为4、矢量积分的变换公式5、关于位矢的运算公式6、正交坐标系中运算的表达式（2）圆柱坐标系（3）球坐标系其中