第3章离散信道及其信道容量.ppt

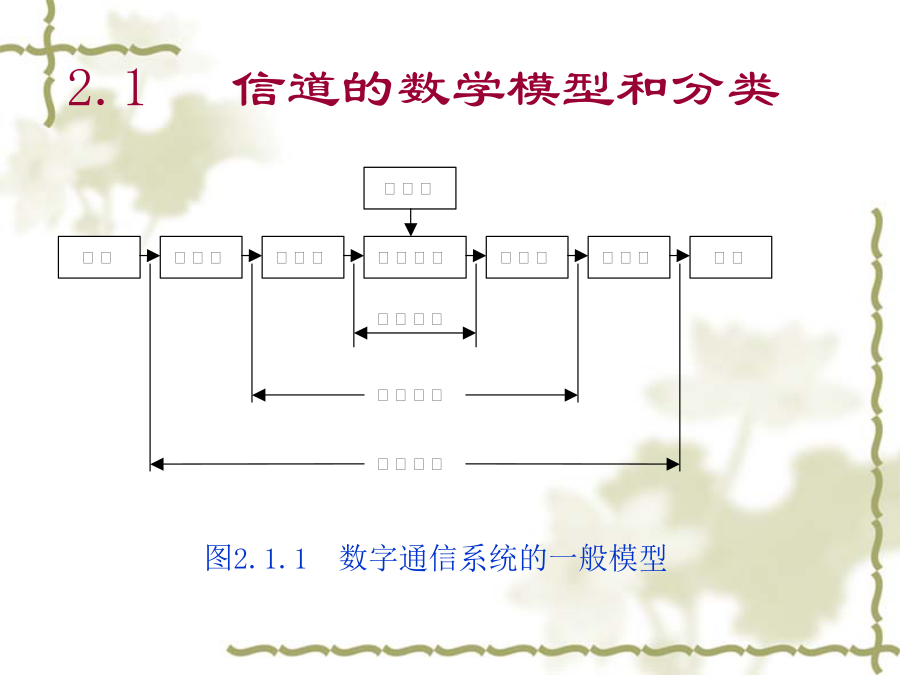
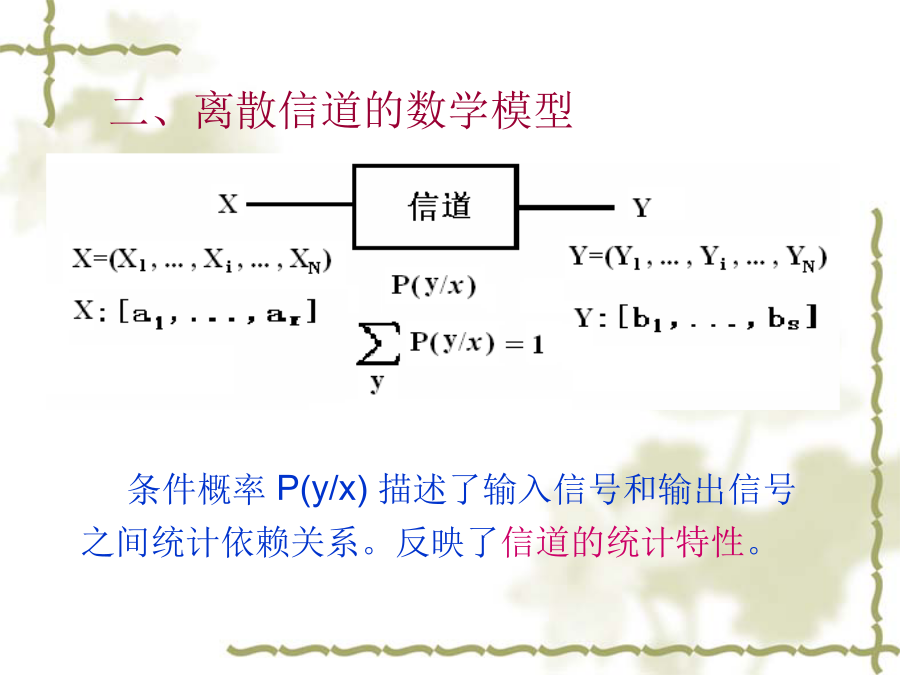
信道的任务是以信号方式传输信息和存储信息。
研究信道中能够传送或存储的最大信息量，即信道容量。2.1信道的数学模型和分类一、信道的分类

根据载荷消息的媒体不同根据信息传输的方式分类中
根据信道的用户多少：两端(单用户)信道
多端(多用户)信道
根据信道输入端和输出端的关联：
无反馈信道
反馈信道
根据信道的参数与时间的关系：
固定参数信道
时变参数信道
根据输入和输出信号的特点：
离散信道
连续信道
半离散或半连续信道
波形信道二、离散信道的数学模型根据信道的统计特性即条件概率P(y/x)的不同，离散信道又可分成三种情况：
无干扰信道
有干扰无记忆信道
有干扰有记忆信道
(1)无干扰(噪声)信道
信道中没有随机性的干扰或者干扰很小，输出信号y与输入信号x之间有确定的、一一对应的关系。即：
y＝f(x)(2)有干扰无记忆信道
信道输入和输出之间的条件概率是一般的概率分布。
如果任一时刻输出符号只统计依赖于对应时刻的输入符号，则这种信道称为无记忆信道。(3)有干扰(噪声)有记忆信道
实际信道往往是既有干扰(噪声)又有记忆的这种类型。
例如在数字信道中，由于信道滤波使频率特性不理想时造成了码字之间的干扰。
在这一类信道中某一瞬间的输出符号不但与对应时刻的输入符号有关，而且还与此以前其他时刻信道的输入符号及输出符号有关，这样的信道称为有记忆信道。三、单符号离散信道信道中有干扰(噪声)存在，可以用传递概率P(bj/ai)来描述干扰影响的大小。
一般简单的单符号离散信道可以用[X,P(y/x),Y]三者加以描述。
其数学模型可以用概率空间[X,P(y/x),Y]描述。当然，也可用下图来描述：[例1]二元对称信道，[BSC，BinarySymmetricalChannel]符号“2”表示接收到了“0”、“1”以外的特殊符号一般离散单符号信道的传递概率可用矩阵形式表示，即研究信道的目的是要讨论信道中平均每个符号所能传送的信息量-----信息传输率R
平均互信息I(X;Y)就是接收到符号Y后平均每个符号获得的关于X的信息量。
所以：
R=I(X;Y)=H(X)–H(X|Y)(比特/符号)一、信道容量的定义

由于平均互信息I(X;Y)是输入随机变量的∩型凸函数，所以对一固定的信道，总存在一种信源，使传输每个符号平均获得的信息量最大。
即存在一个最大的信息传输率------定义为信道容量C即：离散无噪信道有噪无损信道：无噪有损信道所谓对称信道，是指信道矩阵P中每一行都是由同一集合{p1’，p2’，…，ps’}中的诸元素不同排列组成，且每一列也都是由{q1’，q2’，…，qr’}中的诸元素不同排列组成。
具有这种对称信道矩阵的信道称为对称离散信道。
一般s≠r。都不是对称离散信道若输入/输出符号个数相同，都等于r，且信道矩阵为：这一项是固定X＝x时对Y求和，即对信道矩阵的行求和。由于信道的对称性，所以H(Y/X=x)与x无关，为一常数，即在这个信道中，每个符号平均能够传输的最大信息为0.0817比特。
只有当信道的输出符号是等概率分布时才能达到这个最大值。四、离散无记忆N次扩展信道的信道容量一般情况下，消息序列在离散无记忆的N次扩展信道中传输的信息量：
I（X;Y）NC2.3容量—代价函数更一般地，扩展为N阶信道：
输入：X=(x1,x2,x3,……,xn)
输出：Y=(y1,y2,y3,……,yn)

代价：

如果n个输入用联合分布函数为p(X)=p(x1,x2,…,xn)的随机变量X=(X1,X2,…,Xn)来描述，则平均代价定义为：
信道的n阶容量—代价函数Cn(β)为：

该函数的性质:
，Cn(β)只定义在大于βmin的范围内,且是升函数；

所有Cn(β)都是上凸的；
对于任意DMC，Cn(β)=nC1(β)对所有的n和β>=βmin都成立。
信道的容量—代价函数：

对无记忆信道，C(β)=C1(β)。Cmax
如果β足够大,C(β)实际上是一个常数.定义:
Cmax=max{C(β):β>=βmin}
即:Cmax=max{I(X;Y)}

定理2.3如果一个对称DMC有r个输入,s个输出,则输入等概时,DMC达到它的信道容量:
Cmax=logs-H(q0,q1,…,qs-1)
其中：(q0,q1,…,qs-1)是转移概率矩阵的任意一行.