
以解析函数的理论与方法研究电磁学中的一些问题.ppt

天马****23









亲,该文档总共30页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

以解析函数的理论与方法研究电磁学中的一些问题.ppt
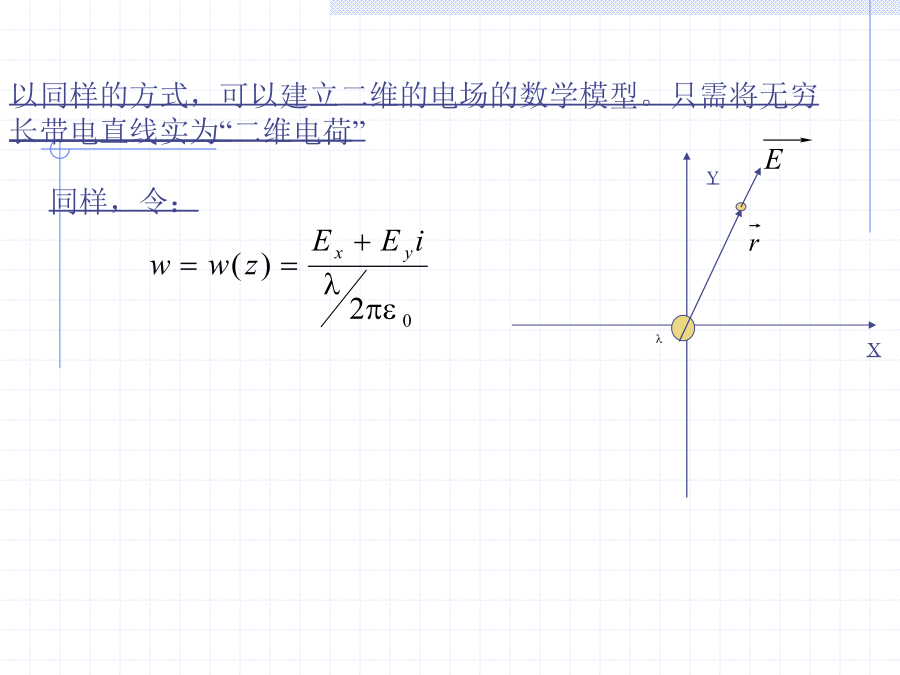
复变函数和电磁学这两门课中一些重要的公式是很相似的,本文试图在一定的程度上发掘其中的联系。主要内容二维场数学模型现把Y-X平面视为复平面,z=x+iy,并令:高斯定理与环路定理取C为一条围绕原点的简单封闭曲线,如果原点处存在无限长的导线(或者带电直线),则由留数定理可得:比较实部虚部即得:上式即是我们熟悉的安培环路定理.而(2)式的意义又何在呢?注意到:显然,稍作推广即可以得到:1.对于磁场中的任意简单封闭曲线C,有由解析的性质得到的一些结论上式的依据是平均值公式3如果平面区域中没有电荷或者没有磁荷,则场

余倾斜理论中的一些问题研究.docx
余倾斜理论中的一些问题研究标题:余倾斜理论研究中的关键问题摘要:余倾斜理论是一种用于分析多元统计数据的方法,已被广泛应用于社会科学研究。本文将探讨余倾斜理论中的一些关键问题,包括理论基础、模型推导、数据解释以及方法应用等方面,旨在提供对余倾斜理论的深入理解。1.引言余倾斜理论是在20世纪70年代提出的一种多元统计方法,最初被应用于心理学研究中。随着时间的推移,余倾斜理论逐渐被应用于社会科学领域,如教育、经济学、管理学等。本文将重点探讨余倾斜理论研究中的关键问题,包括理论基础、模型推导、数据解释以及方法应用

浅谈函数导数在电磁学中的应用.docx
浅谈函数导数在电磁学中的应用函数导数在电磁学中的应用电磁学是物理学的分支之一,研究电荷的相互作用和电磁波的传播等现象,是现代科技发展中不可或缺的一部分。而函数导数在电磁学中的应用更是被广泛应用于各个领域,本文将对其主要应用做一简要的介绍。1.电场强度电场强度是指在某一点上的电场力的大小,通常用E来表示,其大小与电荷密度、电势差等因素有关。在电磁学中,函数导数可以用来计算电场强度的变化率,从而更准确地描述电场的特性。设在某一点上的电场强度E与空间坐标(x,y,z)有关,则其导数可以表示为:∇E=(dE/dx

能带理论中的格林函数方法.docx
能带理论中的格林函数方法标题:格林函数方法在理论物理中的应用摘要:格林函数是理论物理中重要的数学工具之一,广泛应用于量子场论、固体物理、统计物理等领域。本论文将从理论物理的角度出发,探讨格林函数方法的原理、基本性质以及在不同领域中的应用,旨在深入理解格林函数方法在解决物理问题中的重要性和普适性。第一部分:引言引言部分简要介绍格林函数的历史背景和重要性,概述本论文的研究目的和结构,为后续内容做铺垫。第二部分:格林函数的基本原理2.1格林函数的定义和性质介绍格林函数的定义,强调其与物理问题中的关联性。同时介绍

基函数中带形状参数的几何造型理论与方法研究.docx
基函数中带形状参数的几何造型理论与方法研究基函数中带形状参数的几何造型理论与方法研究随着信息技术的飞速发展,计算机在各个领域中得到了广泛的应用。在计算机图形学中,几何造型是一个十分重要的问题,而基函数的使用在几何造型中发挥了非常重要的作用。基函数是一种数学工具,用来描述一个函数在一定区域内的性质。其在求解微分方程、拟合曲线等方面有很多应用。基函数的使用大大增加了几何造型的灵活性和自由度,使得计算机图形学能够更好地模拟真实世界的各种物体和场景。在几何造型中,基函数中带形状参数的方法是一种常用的技术。这种方法
