密度矩阵重整化群-豆柴文库

密度矩阵重整化群.ppt

2024-09-11

10金币

419KB

24页

天马****23

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共24页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

密度矩阵重整化群.ppt

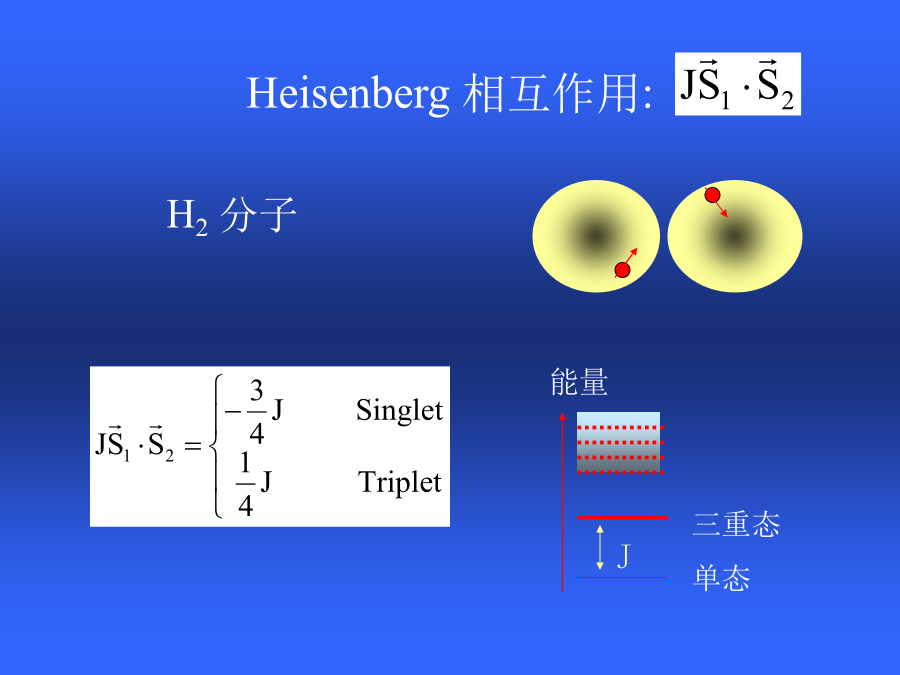
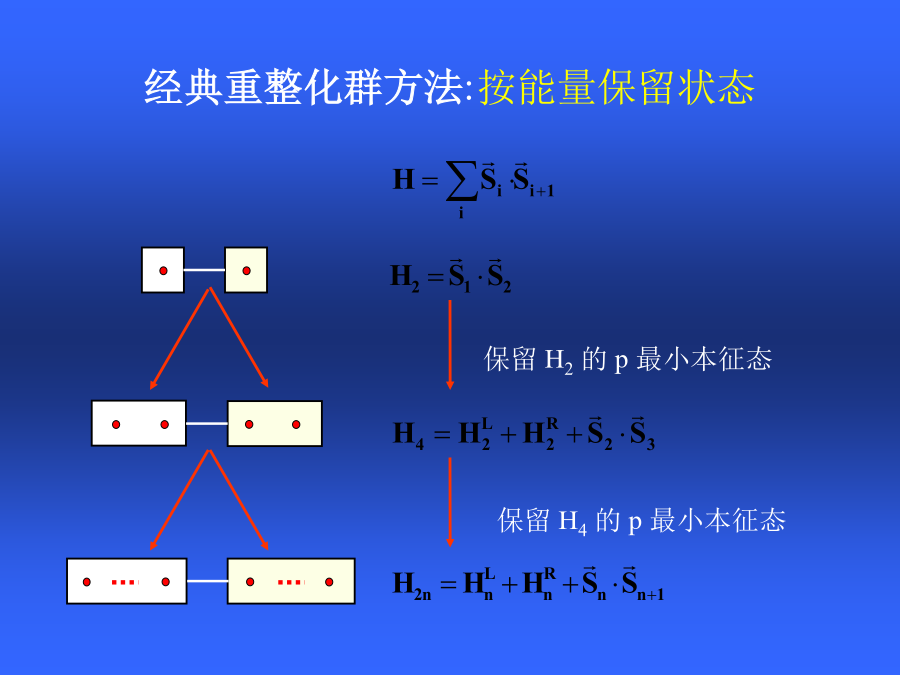
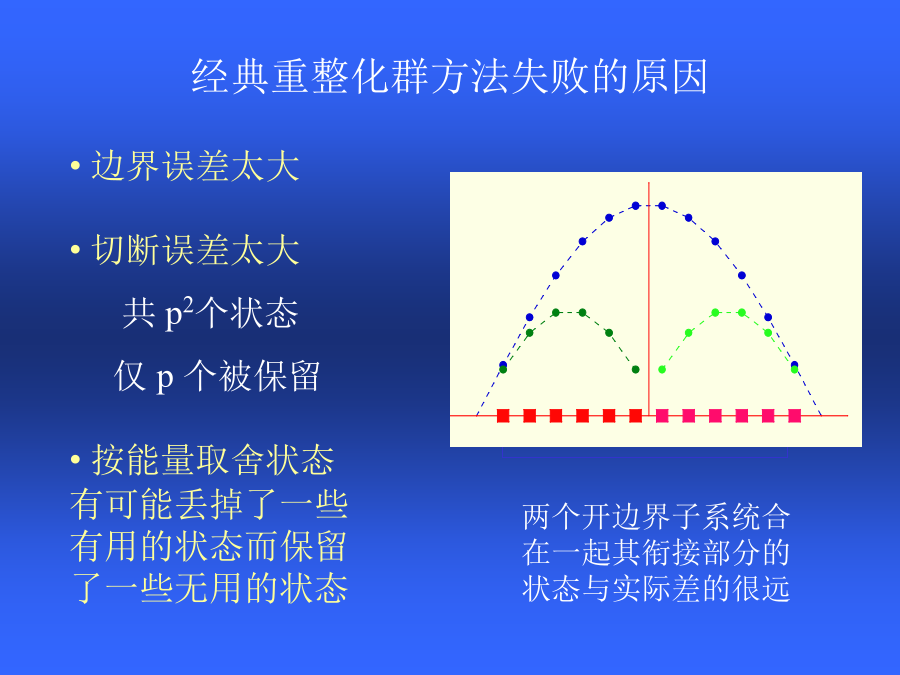
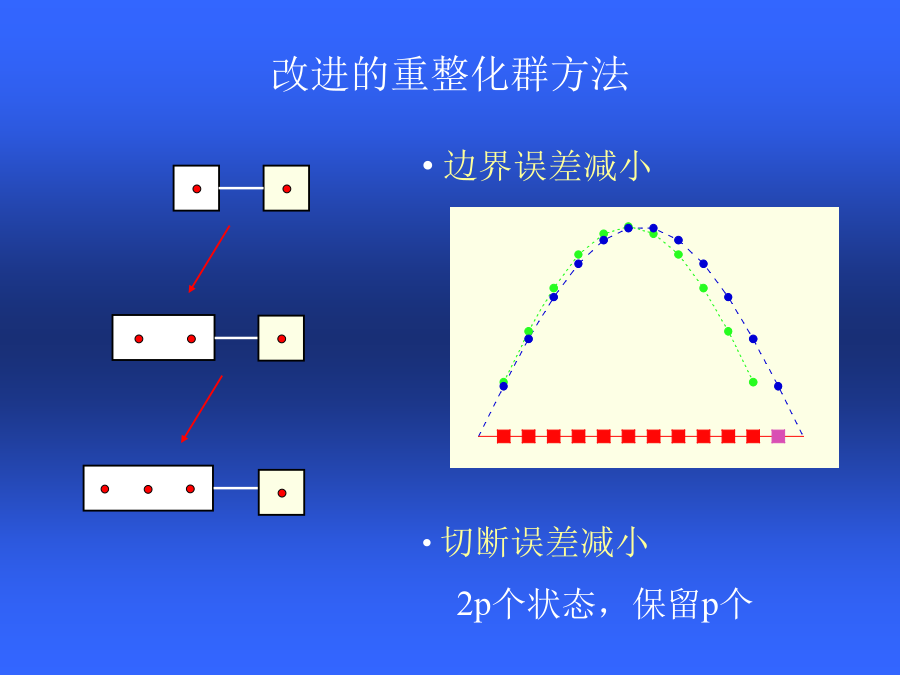
一个多体相互作用系统在某个特定状态(例如基态)下的物理性质困难点：不可微扰S=1/2Heisenberg模型Particleinabox所研究的矩阵的特点重整化群思想经典重整化群方法失败的原因改进的重整化群方法密度矩阵重整化群约化密度矩阵DMRG迭代过程Lanczos方法DMRG与其它方法比较计算量转移矩阵重整化群：有限温度DMRG方法转移矩阵重整化群与DMRG的比较S=1/2Heiserberg模型的磁化率S=1/2Heiserberg模型的关联长度二维密度矩阵重整化群方法Heisenberg模型的基态

2024-09-11

419KB

密度矩阵重整化群及其在凝聚态物理中的应用.ppt

2024-09-11

396KB

密度矩阵重正化群的异构并行优化.docx

密度矩阵重正化群的异构并行优化密度矩阵重正化群（DensityMatrixRenormalizationGroup,DMRG）是一种用于解决强关联量子多体系统的高效方法，被广泛应用于凝聚态物理中的各种问题。随着问题规模的增长，DMRG的计算复杂度会呈指数级增加，因此对DMRG算法的优化至关重要。异构并行（heterogeneousparallelism）则是一种通过充分利用多种硬件资源，如CPU和GPU，来加速计算的方法。本文将介绍DMRG算法及其在密度矩阵重正化群的并行优化方面的应用，并探讨异构并行在D

2024-10-30

10KB

含时密度矩阵重正化群的理论与应用.pptx

含时密度矩阵重正化群的理论与应用目录添加目录项标题含时密度矩阵重正化群的基本理论含时密度矩阵重正化群的定义含时密度矩阵重正化群的数学表达含时密度矩阵重正化群的物理意义含时密度矩阵重正化群的应用领域凝聚态物理高能物理光学材料化学反应动力学含时密度矩阵重正化群的方法与技巧数值计算方法近似技巧收敛性分析误差控制与精度提高含时密度矩阵重正化群的实验验证与结果分析实验验证方法实验结果分析与其他方法的比较应用前景与展望感谢观看

2024-10-03

4.7MB

一维自旋系统热力学性质的转移矩阵重整化群研究的开题报告.docx

一维自旋系统热力学性质的转移矩阵重整化群研究的开题报告一、研究背景与意义在统计物理学中，自旋模型是用于研究金属、磁性体、固体等物质的热力学性质的一种模型。自旋模型在研究材料磁性、热容、磁熵等方面有着重要的应用。自旋模型的研究在催化材料的设计、新材料的探索、无机半导体的制备等领域有着广泛的应用价值。传统的自旋系统研究主要集中在研究两维和三维的自旋系统，而分析一维自旋系统的性质是一个重要而有挑战性的问题。研究一维自旋系统对于了解自旋模型的基本行为和性质具有重要意义。而转移矩阵重整化群是一种重要的分析方法，它可

2024-09-14

11KB