
spss-非线性回归分析.doc

sy****28






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

spss非线性回归分析.docx
课程名称实用统计软件实验项目名称非线性回归分析实验成绩指导老师(签名)日期2011-9-23一.实验目的1.掌握非线性回归的基本原理和算法;2.能够用SPSS软件应用非线性回归模型解决实际问题。二.实验内容与要求1.根据数据金属强度测试.sav利用曲线参数估计法分析金属强度(y)与温度(x)之间的关系。2.实现书上P189中的研究问题。第一步要选中所有的模型,然后根据R-square和拟合曲线标准选择模型!并且要预测到2010年的数据!三.实验步骤1.模型选择(标准:R-square以及拟合曲线的比较)2

spss-非线性回归分析.doc
实验三非线性回归分析(2学时)一、实验重点掌握非线性回归分析的方法。二、实验难点模型的选择及对SPSS软件的输出结果进行分析和整理。三、实验举例例1、对GDP(国内生产总值)的拟合。选取GDP指标为因变量,单位为亿元,拟合GDP关于时间t的趋势曲线。以1981年为基准年,取值为t=1,1998年t=18,1991-1998年的数据如下:年份tGDP年份tGDP14862.41018547.925294.71121617.835934.51226638.1471711334634.458964.414467

基于MATLAB和SPSS的非线性回归分析.docx
基于MATLAB和SPSS的非线性回归分析非线性回归分析是一种广泛运用于数据建模和预测的常见统计方法。其主要用于建立因变量与一个或多个自变量间的函数关系,通过寻找最优的参数拟合数据。在本文中,我们将探讨基于MATLAB和SPSS的非线性回归分析。MATLAB是一种强大的数学软件,其提供了多种用于拟合非线性模型的函数。其中,最常用的函数为curvefittingtoolbox中的“nlinfit”函数。该函数可以自动寻找使得拟合模型与数据拟合度最优的参数,并返回拟合后的结果,以及各个参数的置信度。除此之外,
基于MATLAB和SPSS的非线性回归分析.pdf
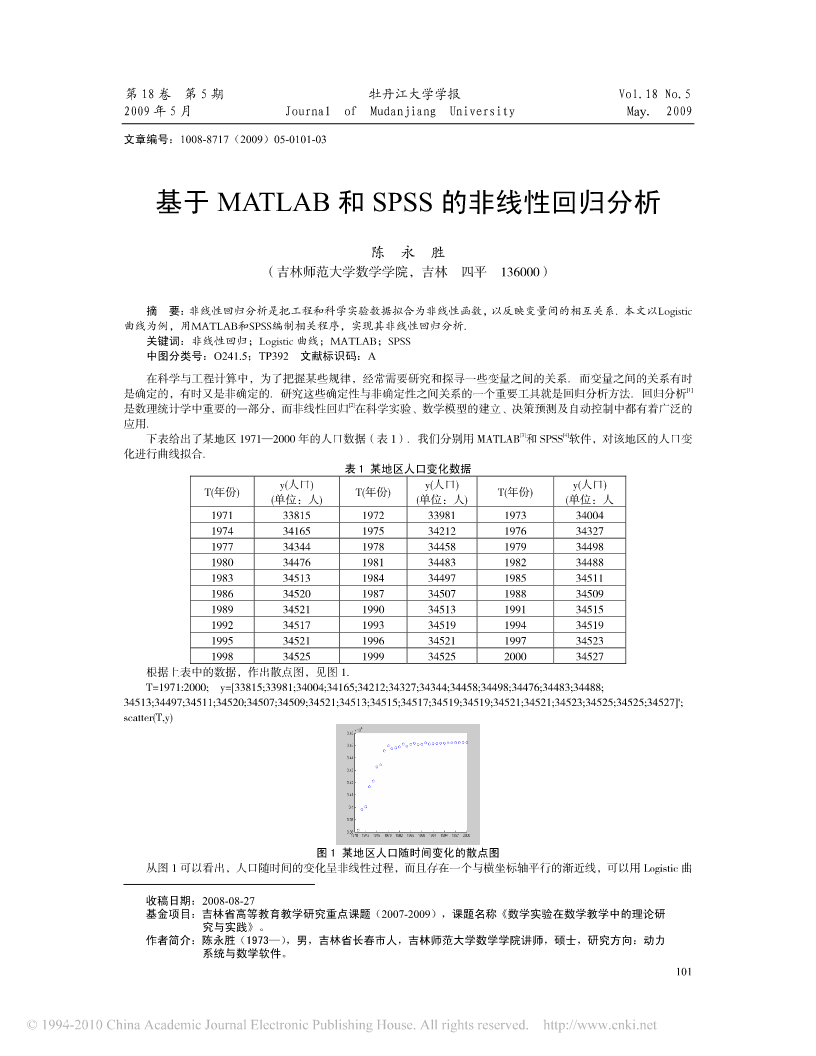
第18卷第5期牡丹江大学学报Vol.18No.52009年5月JournalofMudanjiangUniversityMay.2009文章编号:1008-8717(2009)05-0101-03基于MATLAB和SPSS的非线性回归分析陈永胜(吉林师范大学数学学院,吉林四平136000)摘要:非线性回归分析是把工程和科学实验数据拟合为非线性函数,以反映变量间的相互关系.本文以Logistic曲线为例,用MATLAB和SPSS编制相关程序,实现其非线性回归分析.关键词:非线性回归;Logistic曲线;M

实验六-用SPSS进行非线性回归分析.doc
实验六用SPSS进行非线性回归分析例:通过对比12个同类企业的月产量(万台)与单位成本(元)的资料(如图1),试配合适当的回归模型分析月产量与单位成本之间的关系图1原始数据和散点图分析一、散点图分析和初始模型选择在SPSS数据窗口中输入数据,然后插入散点图(选择Graphs→Scatter命令),由散点图可以看出,该数据配合线性模型、指数模型、对数模型和幂函数模型都比较合适。进一步进行曲线估计:从Statistic下选Regression菜单中的CurveEstimation命令;选因变量单位成本到Dep
