约束优化方法.ppt

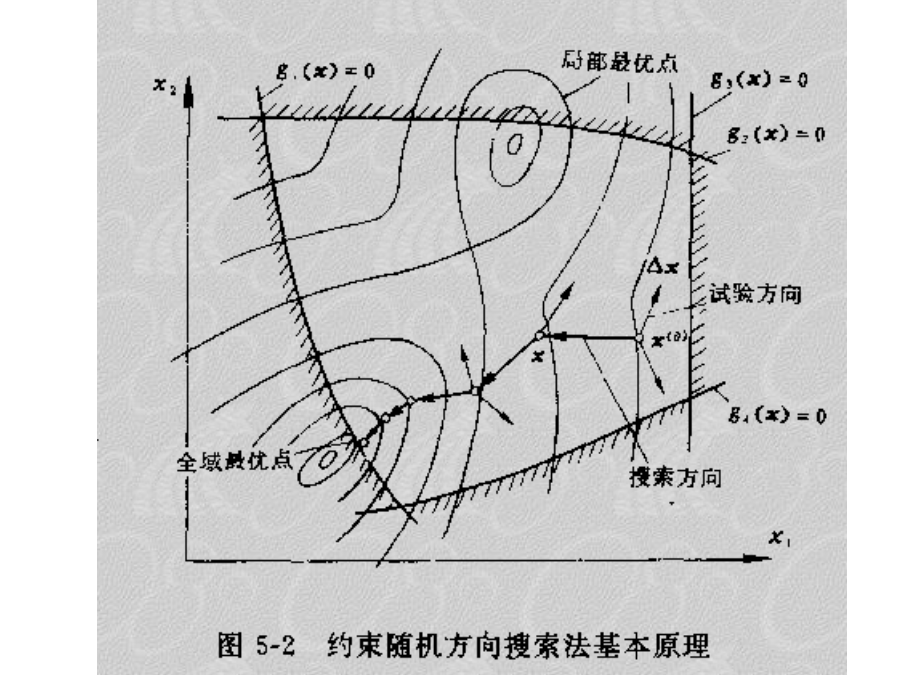
3.2约束优化方法3.2.1约束优化方法概述二、约束优化方法分类(2).间接法3.2.2约束随机方向法采用约束随机方向搜索法的迭代格式为在约束可行域内选取一个初始点x(0)。为了确定本次迭代的搜索方向，以若干个不同方向的向量△x进行试验性的探索，若f(x(0)+△x)＜f(x(0))，则以△x为搜索方向，取适当步长因子，在不破坏约束条件的情况下，前进一步，取得新点x，若f(x)＜f(x(0))，则将起始点移至x点，重复前面的过程。否则需将步长因子缩短，直至取得一个好的可行点。如此周而复始，直至迭代步长已经很小时(即相邻二次迭代点已相距很近)，就结束计算过程，取得约束最优解。显然，约束随机方向搜索法的关键是如何确定二、初始点的选择需要输入对设计变量估计的上限值和下限值，即这样产生的随机点不一定满足所有的约束条件。因此还必须经过可行性条件的检验。若是可行点，即可作为初始点x(0)。若为非可行点，则另取伪随机数再产生一个随机点。直到产生一个可行的随机点为止。采用这种方法来产生可行的初始点，对于中等规模的优化设计问题都比较适用。
三、随机搜索方向的产生取得N个随机单位向量后，可按下式产生N个随机试验点
对于2维问题，其单位向量e(j)的端点分布于单位圆的圆周上。为了尽可能获得较优的搜索方向，应选取适当的步长因子H0。将单位圆缩小或放大，使试验点落在以H0e(j)为半径的圆周上。H0太小，搜索方向的选择将受目标函数局部性质的影响，若H0太大，同样数量的试验点分布在很大圆周上，降低了密度，取得较优的搜索方向的机会也就减少了，影响了收敛速度。对于三维问题，其随机单位向量e(j)的端点位于以单位长为半径的球面上。对于n维问题，则位于超球面上。在这种情况下，其单位随机向量e(j)的分量ei(j)按下式计算：综上所述，在约束随机方向搜索法中，产生随机搜索方向s时应满足的条件是
四、搜索步长的确定
步长因子的确定有两种方法：5．2．2算法的步骤
s．3从初始点x(0)出发，沿可行搜索方向s先以α＝1．3H0的步长移动．若新点是可行点，且目标函数值下降，则继续以α＝1．3α加大步长前进。否则．以α＝0．7α的步长移动。直到目标函数值不再下降同时又不违背约束条件时为止，即完成了一次迭代，将搜索终点x，作为下次搜索的初始点x(0)。
随机方向搜索法的特点