
支持向量机.ppt

sy****28







亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

支持向量机.ppt
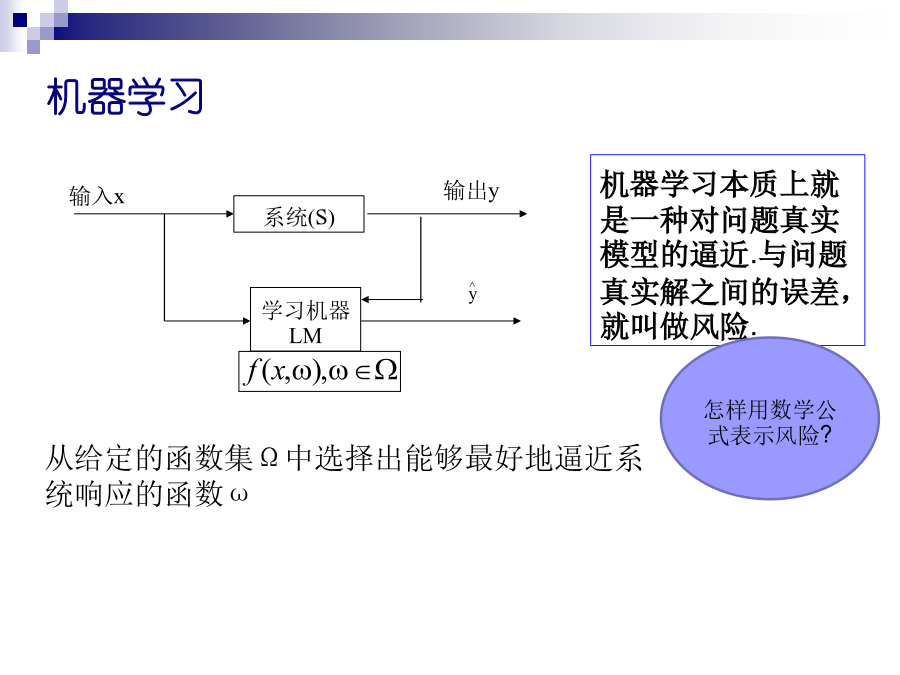
9.3支持向量机支持向量机,一种线性和非线性数据有前途的新划分类方法。巧妙利用向量内积的回旋,通过将非线性核函数将问题变为高维特征空间与低维输入空间的相互转换,解决了数据挖掘中的维数灾难。由于计算问题最终转化为凸二次规划问题,因此挖掘算法是无解或有全局最优解。支持向量机定义概述1.线性可分情形线性可分情形分类面与边界距离(margin)的数学表示:一、线性可分的支持向量(分类)机线性可分的支持向量(分类)机线性可分的支持向量(分类)机线性可分的支持向量(分类)机线性可分的支持向量(分类)机几何意义:超平面

支持向量机.ppt
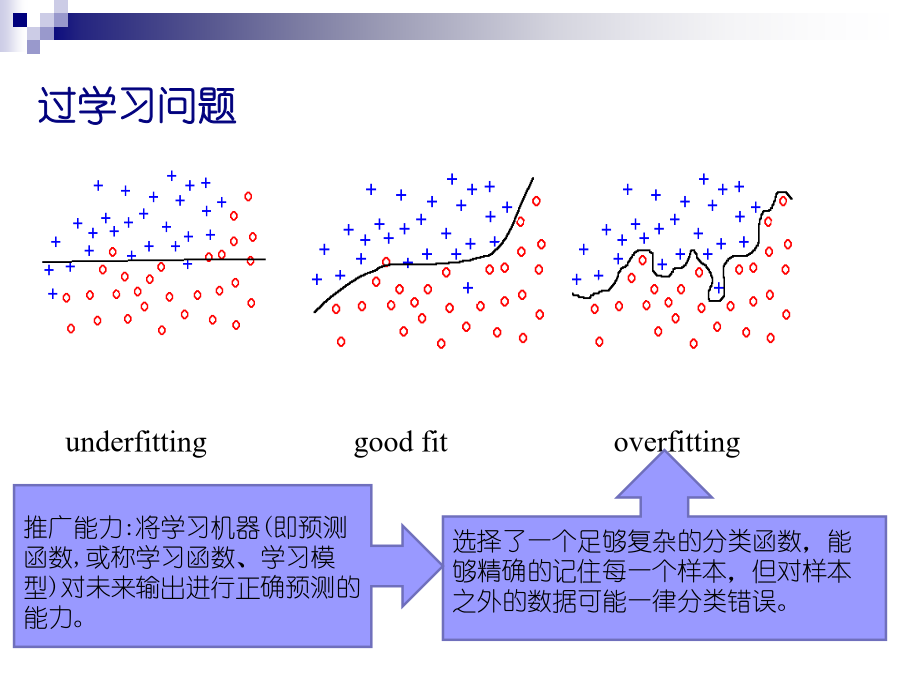
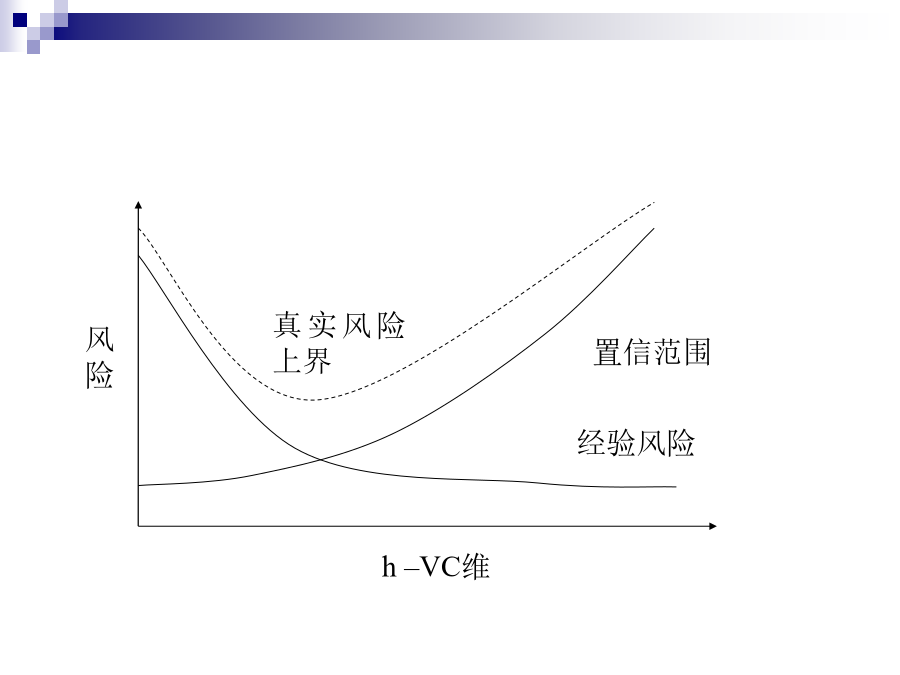
支持向量机(SVM)1.支持向量机简介2.相关概念3.支持向量机原理3.1线性可分3.2线性不可分支持向量机简介支持向量机(SupportVectorMachine)是Vapnik等于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到其他机器学习问题中。支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以期获得最好

支持向量机.doc
第四章支持向量机(SVM——SupportVectorMachine)§4-1.线性分类问题的支持向量机分类问题与机器学习设有两类模式和,是从模式和中抽样得到的训练集,其中、。若属于类,则对应有;若属于类,则对应有;。寻求上的一个实函数,对于任给的未知模式,有或者(4-1)式中为符号函数,称为决策(分类)函数。前两章学过的前向神经元网络和径向基网络,都可以用来解决此类问题。这一章,我们称解决上述问题的方法为“分类机”。当为线性函数时,称为线性分类机;当为非线性函数时,称为非线性分类机。图4-1.样本分布表

支持向量机.doc
支持向量机(SVM)简明学习教程一、最优分类超平面给定训练数据,其中,。若,称为第一类的,;若,称为第二类的,。若存在向量和常数,使得(1),则该训练集可被超平面分开。(一)、平分最近点法求两个凸包集中的最近点,做的垂直平分面x,即为所求。,则,。求,所以,只需求出最小的。算法:1)求解;2)求最优超平面。(二)、最大间隔法附加条件,加上(1)式。记,。使(2)可以说明在(2)下可以得到一个最优超平面,且该超平面是唯一的。如何快速生成一个最优超平面???考虑等价问题:求权向量和,使,且最小。这种写法已经包

《支持向量机》.ppt
支持向量机支持向量机方法是在近年来提出的一种新方法。支持向量机在设计时,需要用到条件极值问题的求解,因此需用拉格朗日乘子理论,但对多数人来说,以前学到的或常用的是约束条件为等式表示的方式,但在此要用到以不等式作为必须满足的条件,此时只要了解拉格朗日理论的有关结论就行。线性可分条件下的支持向量机最优分界面线性可分条件下的支持向量机最优分界面线性可分条件下的支持向量机最优分界面线性可分条件下的支持向量机最优分界面BestLinearSeparator?FindClosestPointsinConvexPlan
