应用MATLAB建模实例---吊门过程仿真.ppt

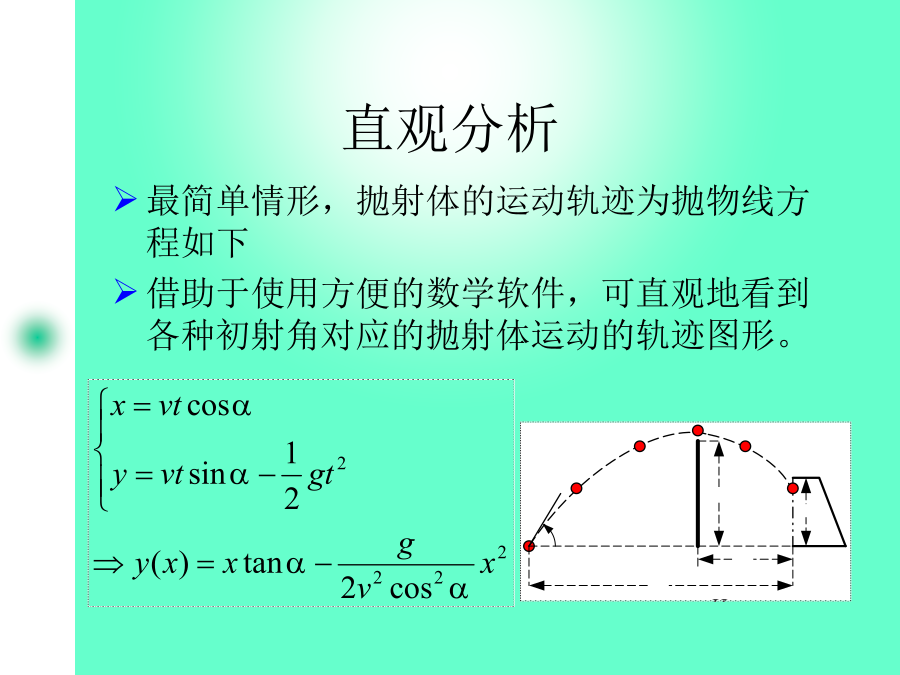
应用MATLAB建模实例——数学也是一门技术数学是一门技术数学及其应用的特征
是一种智能形态的技术
在数学软件的平台上，又表现为一般的物化形态数学建模技术
指数学及其应用于解决实际问题的整个过程
多样性、合理性、具体问题具体分析
艺术性足球比赛中的吊门问题问题分析直观分析最简情形——程序1-1程序1-1之抛射体轨迹函数初步结果初步结果分析——问题的再分析小结：最简情形之假设有空气阻力的情形之一——仅x方向考虑空气阻力问题的解问题的解空气阻力的情形之一——程序2-1-1空气阻力的情形之一——程序2-1-2空气阻力的情形之一的结果及分析改进（一）程序2-1-2修改如下空气阻力的情形之一的结果及分析改进（二）有空气阻力的情形之二——x、y方向均考虑空气阻力y(t)满足如下的常微分方程初值问题有空气阻力的情形之二——程序2-2-1有空气阻力的情形之二——程序2-2-2xt0=v*cos(alpha)*(1-exp(-k*t0))/k;%第一次落地前X向最大飞行距离
vxt0=v*cos(alpha)*exp(-k*t0);%第一次落地X向飞行速度
vyt0=(v*sin(alpha)+g/k)*exp(-k*t0)-g/k;%第一次落地Y向飞行速度
vt0=sqrt(vxt0^2+vyt0^2);%第一次落地飞行速度大小
alpha1=atan(abs(vyt0/vxt0));%计算反弹角度
fori=1:n
ift(i)>t0%判断是落地后进门
tt=t(i)-t0;%计算落地后进门的后半段轨迹
x(i)=xt0+vt0*cos(alpha1)*(1-exp(-k*tt))/k;
y(i)=(vt0*sin(alpha1)+g/k)*(1-exp(-k*tt))/k-g*tt/k;
end
end

%私有函数
functiony=paoshetiy(t,alpha,v,k,g)
y=(v*sin(alpha)+g/k)*(1-exp(-k*t))/k-g*t/k;

functiondy=dpaoshetiy(t,alpha,v,k,g)
dy=(v*sin(alpha)+g/k)*exp(-k*t)-g/k;空气阻力情形之二的结果分析及改进守门员可以移动的情形问题分析守门员可以移动的情形之程序3-1-1fori=1:n;
…………………….%接上部分，分析绘制球飞行轨迹和守门员运动轨迹
i1=floor(Th/0.1)+1;%计算球过球门线时刻的采样点序号
i2=floor(TH/0.1)+1;%计算球过守门员移动的当前位置的采样点序号
ify(i1)>=h|y(i2)<=H|l(i1)==a;%判定是否吊门成功
success(i)=0;
else
success(i)=1;
end
title(['足球比赛中的吊门','初射角=',num2str(alpha(i),6),...
‘球运行时间=',num2str(TH),'成功=',num2str(success(i))]),pause
end
%绘制各射角吊球成功曲线
figure(2)
plot(alpha,success);守门员可以移动的情形之结果谈谈数学建模竞赛及培训有关竞赛及培训的几个方面
“双向”翻译的能力；
想象力、联想力、洞察力和创造能力；
自学能力和使用文献资料的能力；
计算机及相关软件应用能力；
论文写作及表达能力；
组织合作能力。结语谢谢！