
第三章-文法和语言ppt课件.pptx

知识****SA









亲,该文档总共73页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
第三章-文法和语言ppt课件.pptx
知识结构3.1文法的直观概念程序设计语言的描述:语法:程序的结构或形式语义:语言所代表的含义语用:语言的实际应用例如,对于赋值语句x:=a+b*c的非形式描述是:语法:赋值语句=变量+:=+表达式语义:先求右部,然后把结果给左部变量语用:赋值语句可用来计算和保存表达式的值形式化方法:用一整套带有严格规定的符号体系来描述问题的理论和方法形式语言:一种不考虑含义的符号语言程序设计语言的语义分成:静态语义:是一系列限定规则,并确定哪些合乎语法的程序是合适的动态语义(运行语义、执行语义):表明程序要做什么,要计算

二文法和语言PPT课件.ppt
第二章文法和语言2.1语言和文法的直观概念2.2符号和符号串2.3文法和语言的形式定义2.4文法的类型2.5上下文无关文法及其语法树2.6句型的分析2.1语言和文法的直观概念语义(semantics)分类:静态语义:一系列限定规则,确定哪些合乎语法的程序是合适的动态语义:表明程序要做什么描述工具:指称语义,操作语义等作用:检查类型匹配,变量作用域等文法的直观概念例:“我是大学生”是汉语的一个句子汉语句子的构成规则表示如下:〈句子〉∷=〈主语〉〈谓语〉〈主语〉∷=〈代词〉|〈名词〉〈代词〉∷=我|你|他〈名

第三章 文法和语言.ppt
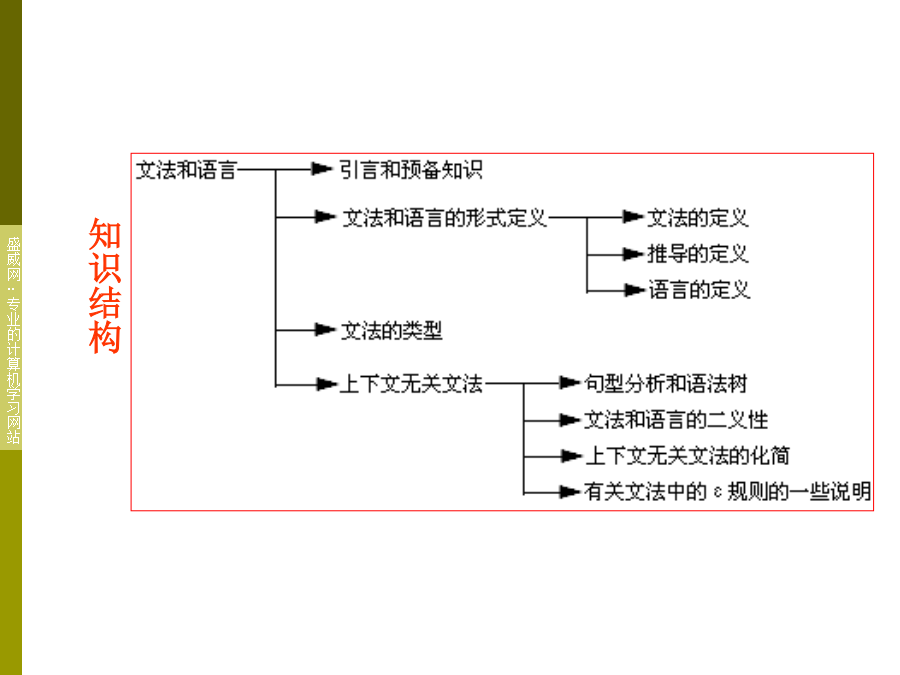
2024/8/21课前思考学习目标学习指南难重点知识结构引言和预备知识语法任何语言程序都可以看成是一定字符集(字母表)上的字符串语法使得这串字符形成一个形式上正确的程序语法=词法规则+语法规则例如:0.5*x1+c0.5、x1、c、*、+是语言的单词符号0.5*x1+c是语言的语法单位词法单词符号语言中具有独立意义的最基本结构词法规则词法规则规定了字母表中哪些字符串是单词符号单词符号一般包括:常数、标识符、基本字、算符、界限符等我们用正规式和有限自动机理论来描述词法结构和进行词法分析语法单词符号语法单位表

编译原理第三章文法和语言.ppt
第三章文法和语言课前思考学习目标学习指南难重点知识结构引言和预备知识语法任何语言程序都可以看成是一定字符集(字母表)上的字符串语法使得这串字符形成一个形式上正确的程序语法=词法规则+语法规则例如:0.5*x1+c0.5、x1、c、*、+是语言的单词符号0.5*x1+c是语言的语法单位词法单词符号语言中具有独立意义的最基本结构词法规则词法规则规定了字母表中哪些字符串是单词符号单词符号一般包括:常数、标识符、基本字、算符、界限符等我们用正规式和有限自动机理论来描述词法结构和进行词法分析语法单词符号语法单位表达

编译原理 第三章 文法和语言.ppt
2024/8/20课前思考学习目标学习指南难重点知识结构引言和预备知识语法任何语言程序都可以看成是一定字符集(字母表)上的字符串语法使得这串字符形成一个形式上正确的程序语法=词法规则+语法规则例如:0.5*x1+c0.5、x1、c、*、+是语言的单词符号0.5*x1+c是语言的语法单位词法单词符号语言中具有独立意义的最基本结构词法规则词法规则规定了字母表中哪些字符串是单词符号单词符号一般包括:常数、标识符、基本字、算符、界限符等我们用正规式和有限自动机理论来描述词法结构和进行词法分析语法单词符号语法单位表
