
内压薄壁圆筒与封头的强度设计.ppt

yy****24









亲,该文档总共55页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

内压薄壁圆筒与封头的强度设计.ppt
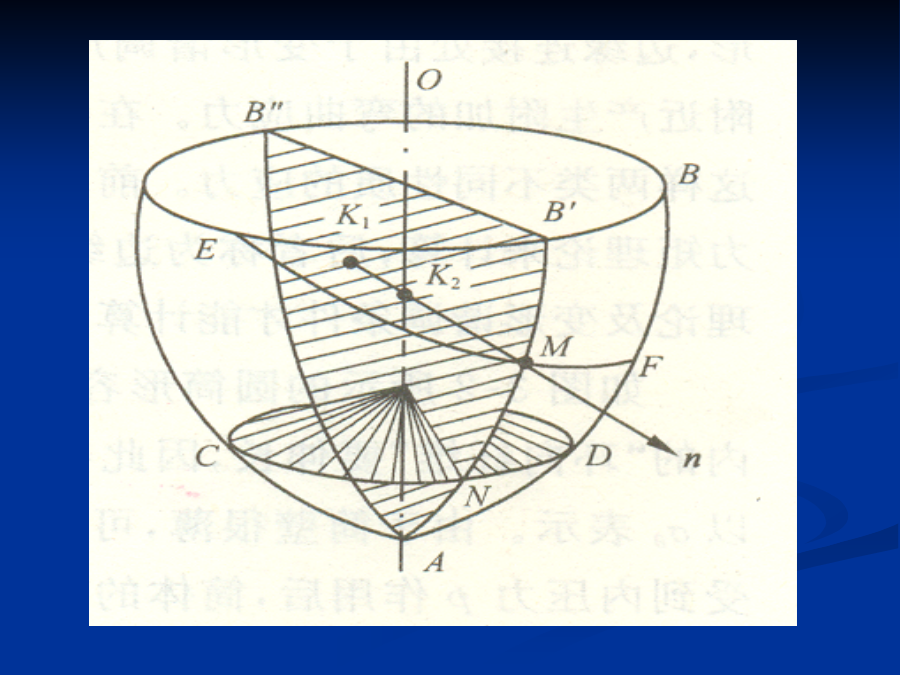
第三章内压薄壁圆筒与封头的强度设计第三章内压薄壁圆筒与封头的强度设计第三章内压薄壁圆筒与封头的强度设计第三章内压薄壁圆筒与封头的强度设计回转壳体:是指壳体中间面是由直线或平面曲线绕其同一平面的轴线旋转一周而形成的壳体。例如与回转轴平行的直线绕轴旋转一周形成圆柱壳;半圆形曲线绕直径旋转一周形成球壳。回转壳体:是指壳体中间面是由直线或平面曲线绕其同一平面的轴线旋转一周而形成的壳体。例如与回转轴平行的直线绕轴旋转一周形成圆柱壳;半圆形曲线绕直径旋转一周形成球壳。中间面:具有一定厚度的旋转壳体,平分其厚度的面称为

内压薄壁圆筒与封头的强度设计.ppt
内压薄壁圆筒与封头的强度设计旧压力容器厚度进行强度校核的意义判定在下一个检验周期内或在剩余寿命期间内,容器是否还能在原设计条件下安全使用的条件当容器已被判定不能在原设计条件下使用时,应通过强度计算,提出容器监控使用当容器针对某一使用条件需要判废时,应提出判废依据根据薄膜理论进行应力分析,确定薄膜应力状态下的主应力根据弹性失效的设计准则,应用强度理论确定应力的强度判据对于封头,考虑到薄膜应力的变化和边缘应力的影响,按壳体中的应力状况在公式中引进应力增强系数根据应力强度判据,考虑腐蚀等实际因素导出具体的计算公

内压薄壁圆筒与封头的强度设计ppt课件.ppt
第四章内压薄壁圆筒与封头的强度设计第四章内压薄壁圆筒与封头的强度设计第四章内压薄壁圆筒与封头的强度设计4.1强度设计的基本知识4.1强度设计的基本知识4.1强度设计的基本知识4.1强度设计的基本知识4.1强度设计的基本知识4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计4.2内压薄壁圆壳体与球壳的强度设计

第九章-内压薄壁圆筒与封头的强度设计.ppt
NanjingUniversityofTechnology第九章内压薄壁圆筒与封头的强度设计9.1.1关于弹性失效的设计准则容器上一处的最大应力达到材料在设计温度下的屈服点,该容器即告破坏。(中低压薄壁容器)强度安全条件:9.1.2强度理论及其相应的强度条件第三强度理论的强度条件为:9.2内压薄壁圆筒壳与球壳的强度设计9.2.1强度计算公式依据第三强度理论,强度公式为:内压圆筒强度计算公式:在公式(9-2)基础上,考虑到钢板的负偏差C(钢板在轧制时产生了偏差)——名义壁厚公式:式中δe——有效壁厚,δe=

第九章-内压薄壁圆筒与封头的强度设计.ppt
NanjingUniversityofTechnology第九章内压薄壁圆筒与封头的强度设计9.1.1关于弹性失效的设计准则容器上一处的最大应力达到材料在设计温度下的屈服点,该容器即告破坏。(中低压薄壁容器)强度安全条件:9.1.2强度理论及其相应的强度条件第三强度理论的强度条件为:9.2内压薄壁圆筒壳与球壳的强度设计9.2.1强度计算公式依据第三强度理论,强度公式为:内压圆筒强度计算公式:在公式(9-2)基础上,考虑到钢板的负偏差C(钢板在轧制时产生了偏差)——名义壁厚公式:式中δe——有效壁厚,δe=
