
塑性内力重分布PPT.ppt

天马****23







亲,该文档总共26页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

塑性内力重分布PPT.ppt
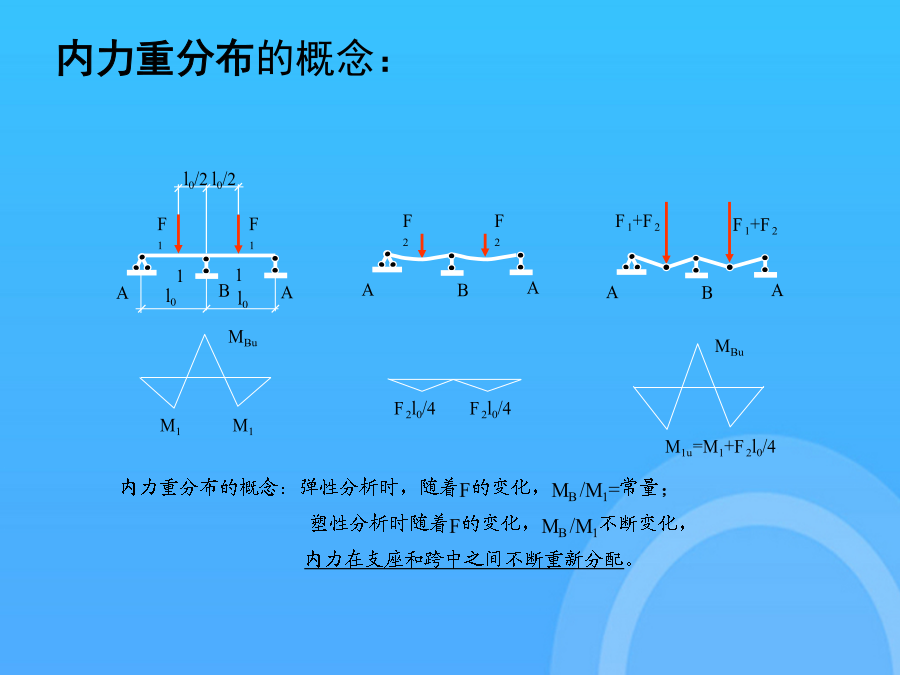
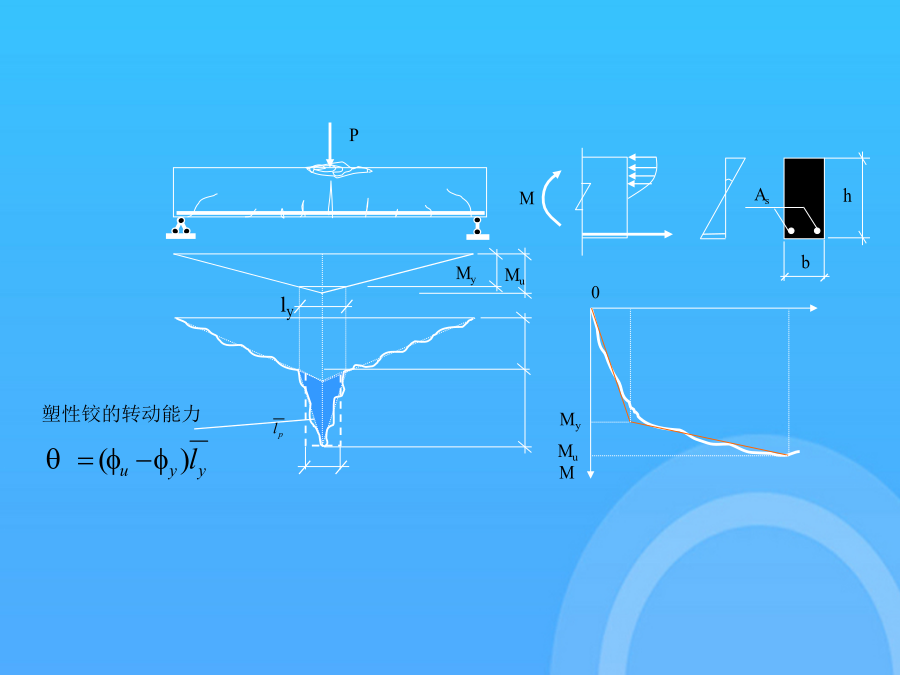
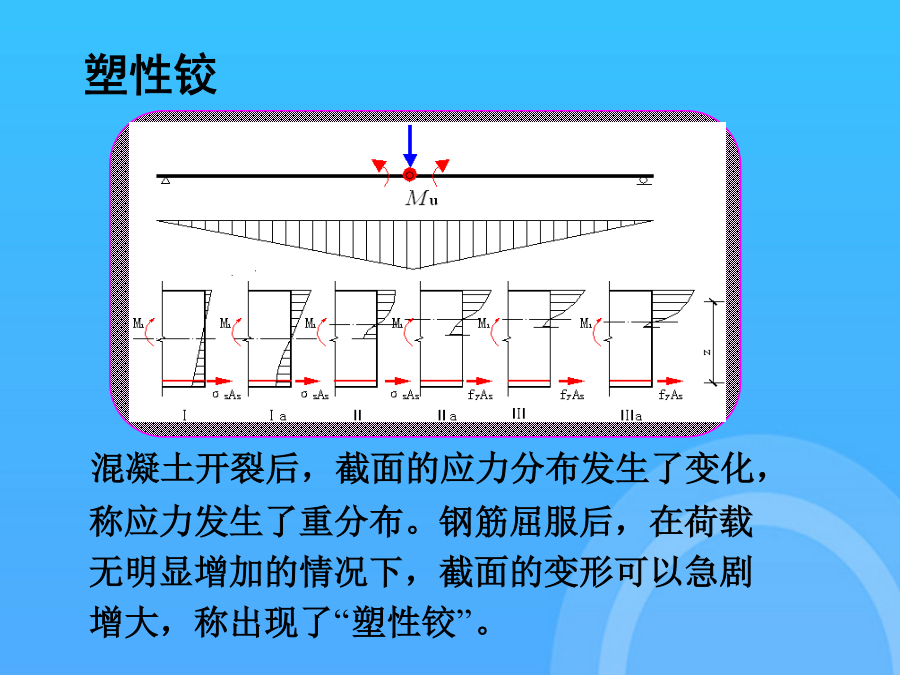
塑性内力重分布超静定结构塑性内力重分布的概念1.应力重分布与内力重分布2.钢筋混凝土受弯构件的塑性铰3.钢筋混凝土超静定结构的内力重分布4.影响内力重分布的因素1.应力重分布与内力重分布应力重分布---截面高度上应力分布不再是直线(线弹性)。(静定与超静定都存在)内力重分布---超静定结构各截面内力关系不再遵循线弹性关系。(原因:超静定结构弹性阶段各截面内力关系取决于弹性刚度,在开裂阶段刚度下降,计算简图发生变化。)内力重分布的概念:由于内力重分布,超静定钢筋混凝土结构的实际承载能力往往比按弹性方法分析的

塑性内力重分布ppt课件.ppt
1超静定结构塑性内力重分布的概念1.应力重分布与内力重分布2.钢筋混凝土受弯构件的塑性铰3.钢筋混凝土超静定结构的内力重分布4.影响内力重分布的因素1.应力重分布与内力重分布应力重分布---截面高度上应力分布不再是直线(线弹性)。(静定与超静定都存在)内力重分布---超静定结构各截面内力关系不再遵循线弹性关系。(原因:超静定结构弹性阶段各截面内力关系取决于弹性刚度,在开裂阶段刚度下降,计算简图发生变化。)内力重分布的概念:由于内力重分布,超静定钢筋混凝土结构的实际承载能力往往比按弹性方法分析的高,故按考虑

塑性内力重分布.pptx
塑性内力(nèilì)重分布1.应力重分布(fēnbù)与内力重分布(fēnbù)应力重分布---截面高度上应力分布不再是直线(zhíxiàn)(线弹性)。(静定与超静定都存在)内力重分布---超静定结构各截面内力关系不再遵循线弹性关系。(原因:超静定结构弹性阶段各截面内力关系取决于弹性刚度,在开裂阶段刚度下降,计算简图发生变化。)l0由于内力重分布,超静定钢筋混凝土结构的实际承载能力往往比按弹性方法分析的高,故按考虑内力重分布方法设计,可进一步发挥结构的承载力储备,节约材料,方便施工;同时研究和掌握内力

塑性内力重分布.ppt
11.2.4超静定结构塑性内力重分布的概念1.应力重分布与内力重分布2.钢筋混凝土受弯构件的塑性铰3.钢筋混凝土超静定结构的内力重分布4.影响内力重分布的因素1.应力重分布与内力重分布应力重分布---截面高度上应力分布不再是直线(线弹性)。(静定与超静定都存在)内力重分布---超静定结构各截面内力关系不再遵循线弹性关系。(原因:超静定结构弹性阶段各截面内力关系取决于弹性刚度,在开裂阶段刚度下降,计算简图发生变化。)l0由于内力重分布,超静定钢筋混凝土结构的实际承载能力往往比按弹性方法分析的高,故按考虑内力

塑性内力重分布教案.pptx
会计学超静定结构塑性内力重分布的概念1.应力重分布与内力重分布2.钢筋混凝土受弯构件的塑性铰3.钢筋混凝土超静定结构的内力重分布4.影响内力重分布的因素1.应力重分布与内力重分布应力重分布---截面高度上应力分布不再是直线(线弹性)。(静定与超静定都存在)内力重分布---超静定结构各截面内力关系不再遵循线弹性关系。(原因:超静定结构弹性阶段各截面内力关系取决于弹性刚度,在开裂阶段刚度下降,计算简图发生变化。)内力重分布的概念:由于内力重分布,超静定钢筋混凝土结构的实际承载能力往往比按弹性方法分析的高,故按
