第二章--流体的热力学性质.ppt

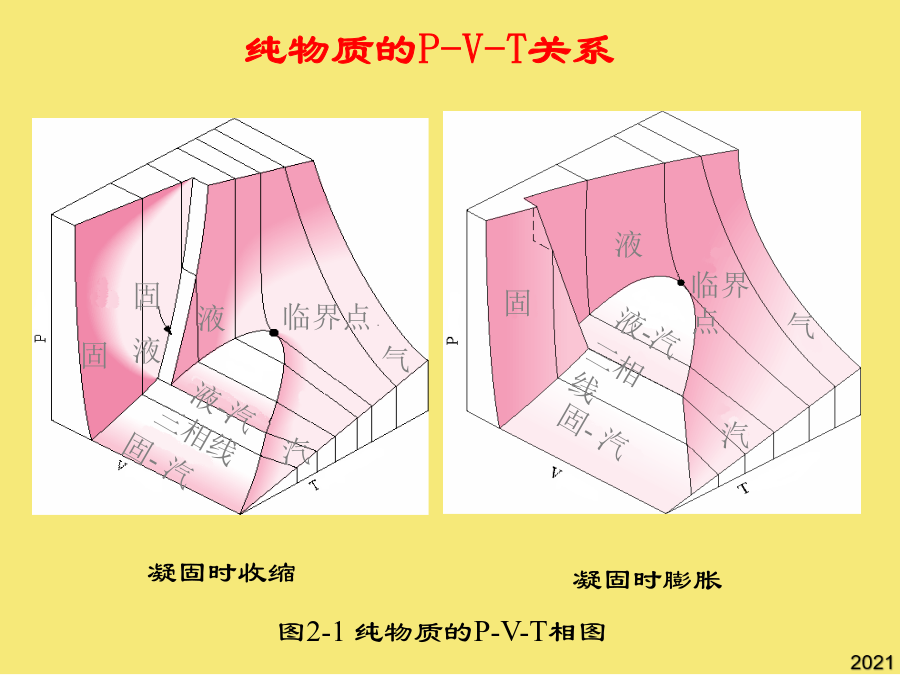
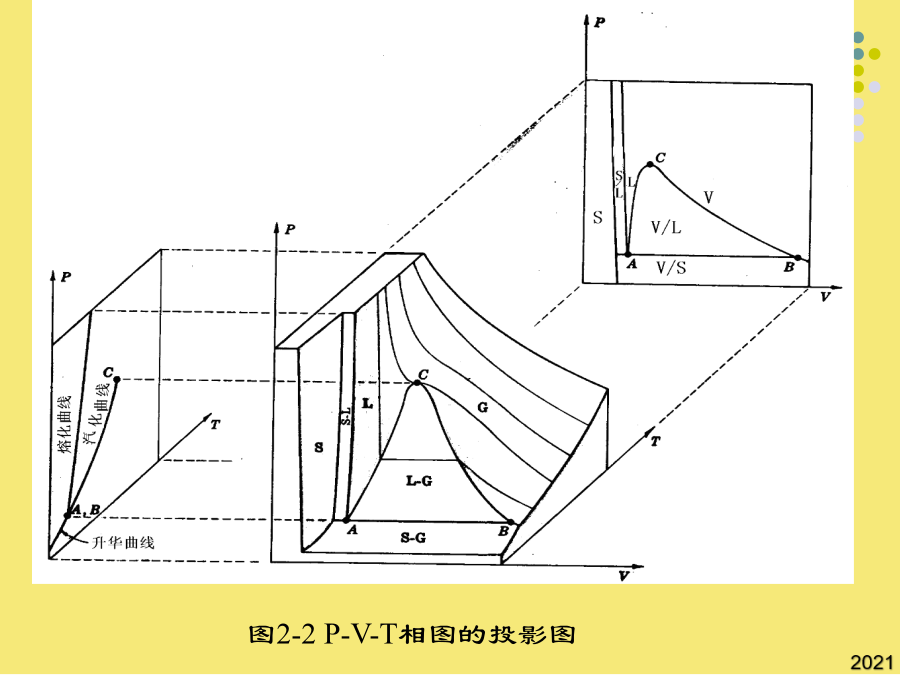
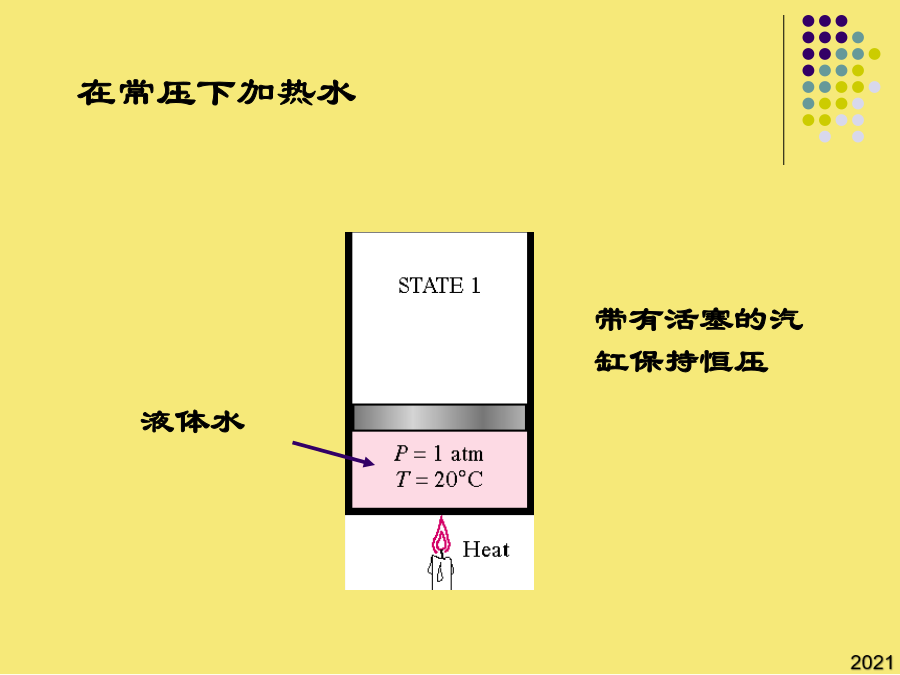
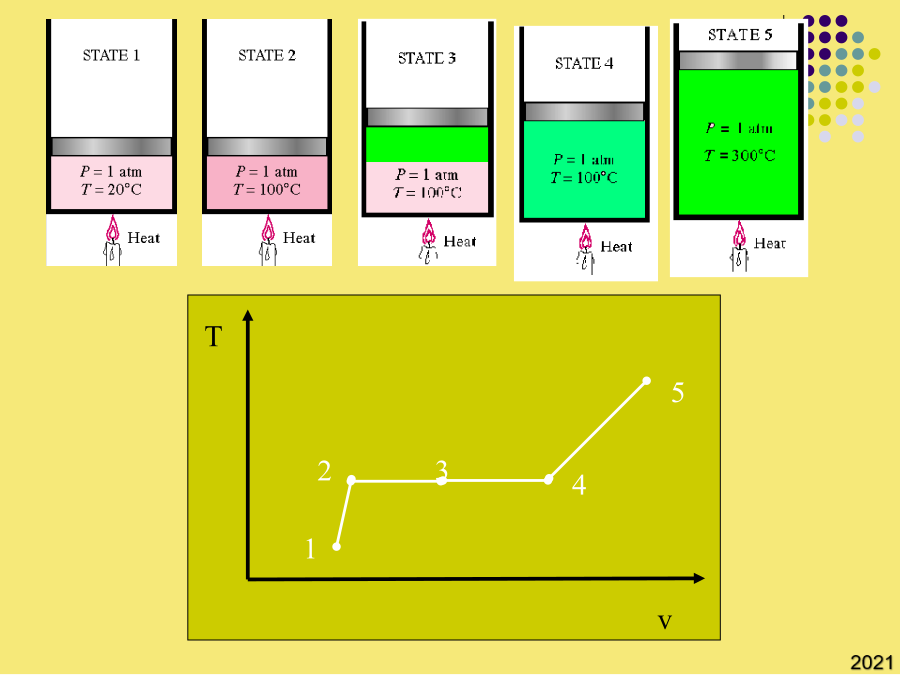
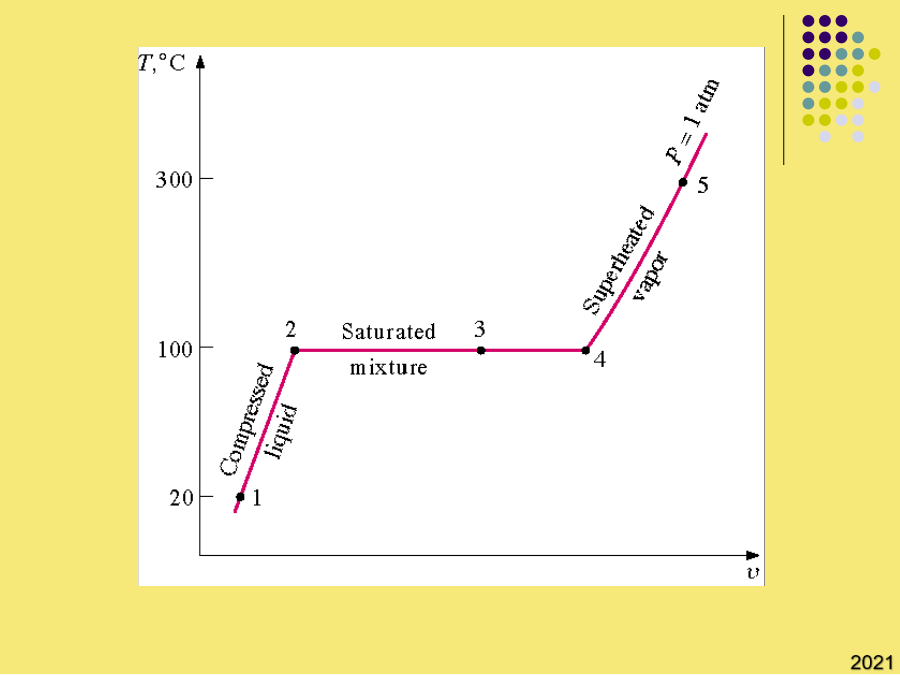
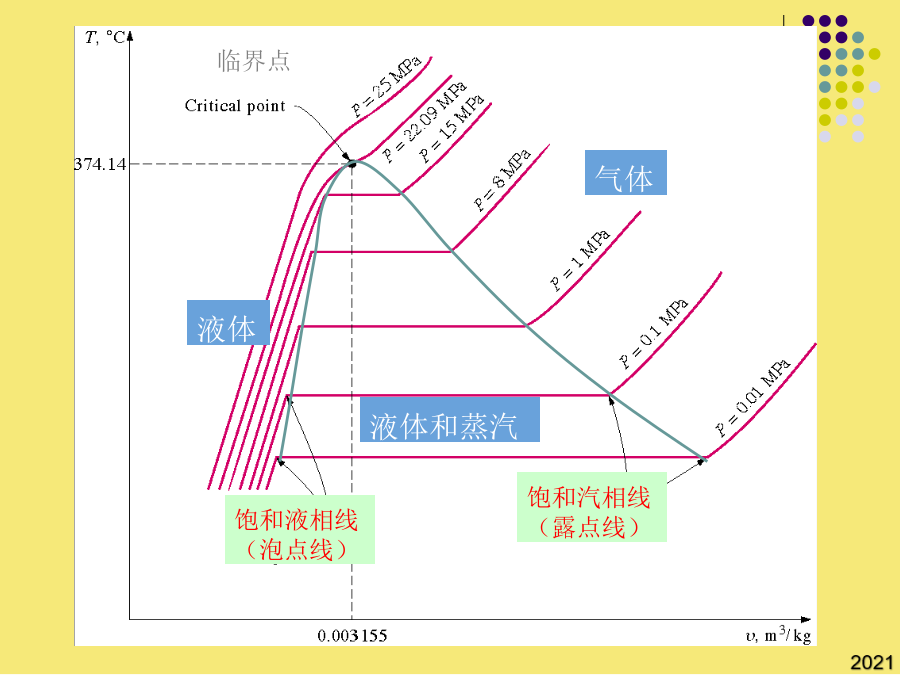
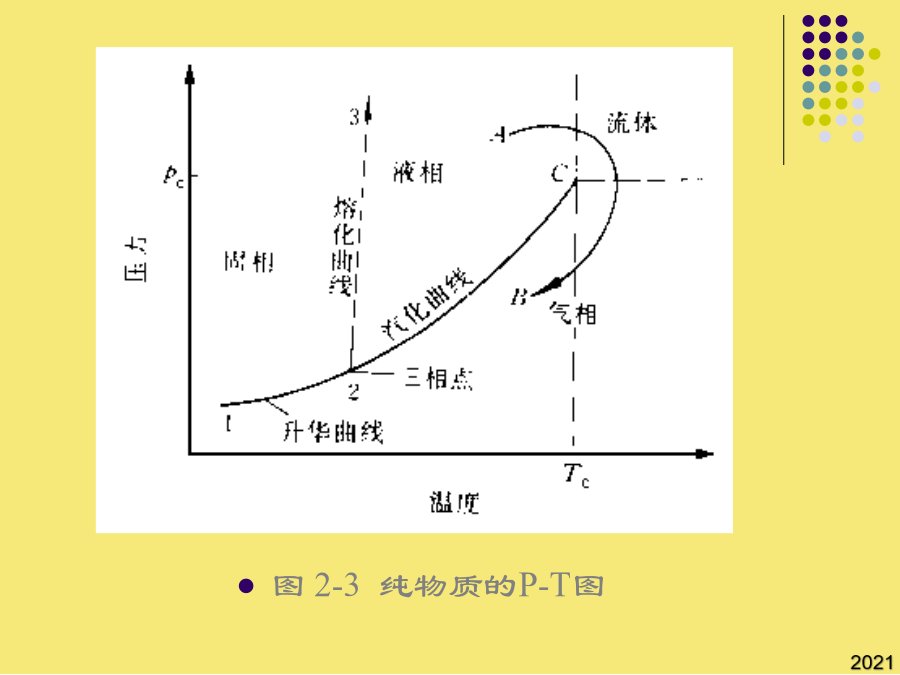
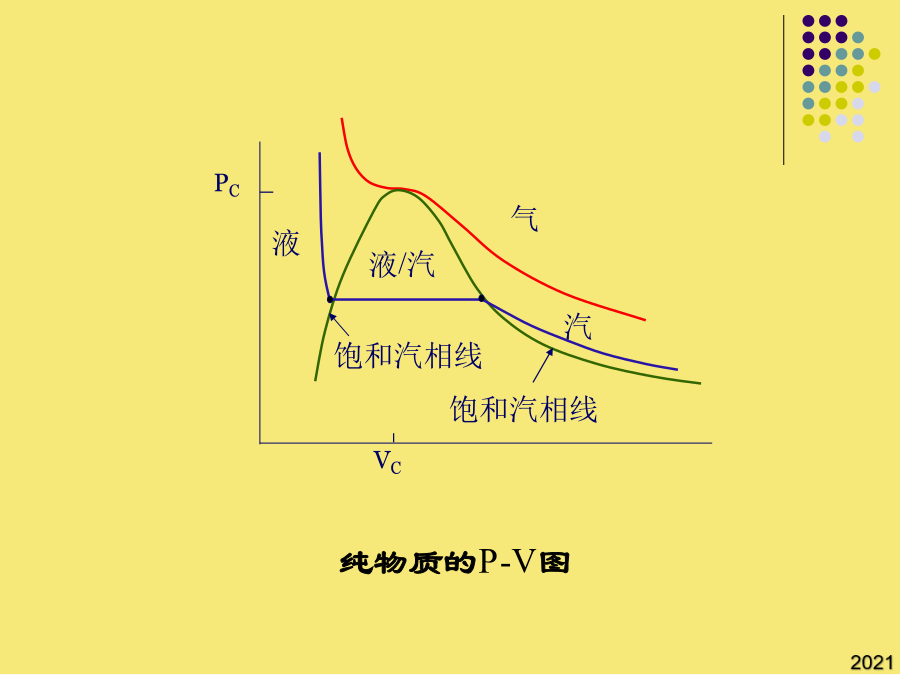
第二章流体的热力学性质2流体的P-V-T关系沿用了SRK方程(Tr,)的形式；
(b)用普遍化压缩因子关联；
1955年，pitzer提出了以偏心因子ω作为第三参数的关系式：
②非球形分子的直线都位于球形分子的直线下面，
Zc，更接近于实际情况，虽较真实情况仍有差别，但PR方程计算液相体积的准确度较SRK确有了明显的改善；
当T>Tc时，立方型状态方程有一个实根，它是气体容积。
球形分子(Ar、Kr、Xe等)ω=0；
(b)用普遍化压缩因子关联；
纯物质的P-V-T关系
如第二Virial系数反映了两分子间的相互作用，
Pitzer提出的三参数普遍化关系式有两种，一种是普维法，另一种是普压法。
丁烯饱和蒸汽
(1)由统计力学进行理论计算
Virial方程的几种形式
Pitzer提出的三参数普遍化关系式有两种，一种是普维法，另一种是普压法。
当T<Tc时，高压下立方型状态方程有一个实根，它是液体容积。图2-2P-V-T相图的投影图在常压下加热水T液体和蒸汽图2-3纯物质的P-T图纯物质的P-V图在临界点C：2.2状态方程理想气体方程理想气体方程的应用
在较低压力和较高温度下可用理想气体方程进行计算。
为真实气体状态方程计算提供初始值。
判断真实气体状态方程的极限情况的正确程度，当或者时，任何的状态方程都还原为理想气体方程。Virial方程微观上Virial系数反映了分子间的相互作用，
如第二Virial系数反映了两分子间的相互作用，
第三Virial系数反映了三分子间的相互作用等等。
宏观上，Virial系数仅是温度的函数。Virial系数的获取
(1)由统计力学进行理论计算
目前应用很少立方型状态方程立方型状态方程的根及其求解方法RK方程立方型状态方程的求根方法：
（1）三次方程求根公式；
（2）迭代法。
简单迭代法求立方型状态方程的根(以RK方程为例说明，其它立方型状态方程求解根方法类似。）(1)蒸汽的摩尔体积(2)液体的摩尔体积SRK方程与RK方程相比，SRK方程大大提高了表达纯物质汽液平衡的能力，使之能用于混合物的汽液平衡计算，故在工业上获得了广泛的应用。Peng-Robinson（PR）方程特点：
Zc，更接近于实际情况，虽较真实情况仍有差别，但PR方程计算液相体积的准确度较SRK确有了明显的改善；
能同时适用于汽、液两相；
计算常数需要Tc,Pc和；
沿用了SRK方程(Tr,)的形式；
在工业中得到广泛应用。多常数状态方程2.3对应态原理的应用2.3.1普遍化状态方程R-K方程普遍化S-R-K方程普遍化例题2-3
分别用R-K方程和S-R-K方程的普遍化计算360K、1.541MPa下异丁烷蒸气的压缩因子，已知由实验数据求出的Z实=0.7173。两参数对比态原理认为在相同的对比温度和
对比压力下，任何气体或液体的对比体积(或
压缩因子)是相同的。
Vr=f1(Tr，Pr)
由于
2.3.3以ω为第三参数的对比态原理Pitzer对大量的物质进行了试验，并发现：
①球形分子（非极性）氩、氪、氙的斜率相同，且在Tr时：偏心因子的物理意义为：其值的大小，是反映物质分子形状与物质极性大小的量度。球形分子(Ar、Kr、Xe等)ω=0；非球形分子ω>0。
根据以上结论，Pitzer提出了两个非常有用的普遍化关系式。一种是以压缩因子的多项式表示的普遍化关系式(简称普压法)，一种是以两项维里方程表示的普遍化第二维里系数关系式(简称为普维法)。三参数对应态原理的表达式：
以压缩因子的多项式表示的普遍化关系式(普压法)Pitzer提出的三参数普遍化关系式有两种，一种是普维法，另一种是普压法。运用这两种方法，要注意它们的应用范围，根据实际条件，选择其中一种方法进行计算。
应用范围：以图中的曲线为界，当Tr，Pr的对应点落在曲线上方时，用普维法；落在下方时用普压法；当求P时，Pr未知，用Vr判据，Vr>=2，用普维法直接计算，而Vr<2时，用普压法迭代求取。例：计算1kmol乙烷在382K、21.5MPa时的体积。解：查表得：2.3.4普遍化Virial方程例2-4试用下列三种方法计算510K、2.5MPa下正丁烷的摩尔体积。已知实验值为1.4807m3·kmol-1。(a)用理想气体方程；(b)用普遍化压缩因子关联；(c)用普遍化维里系数关联。2.4真实气体混合物2.4.1混合规则与虚拟临界参数法虚拟对比参数：普劳斯尼茨(Prausnitz-Gunn)改进规则在此基础上，可以按纯组分气体pVT性质的计算方法进行气体混合物计算。具体计算过程如下：混合物的维里方程为2.5液体容积性质2.6纯流体的热力学性质适用于只有体积功存在的均相封闭系统，另外热力性质间有如下定义式：熵和焓的计算式例2-4试用下列三种方法计算510K、2.
三参数对