图像处理中的傅里叶变换.ppt

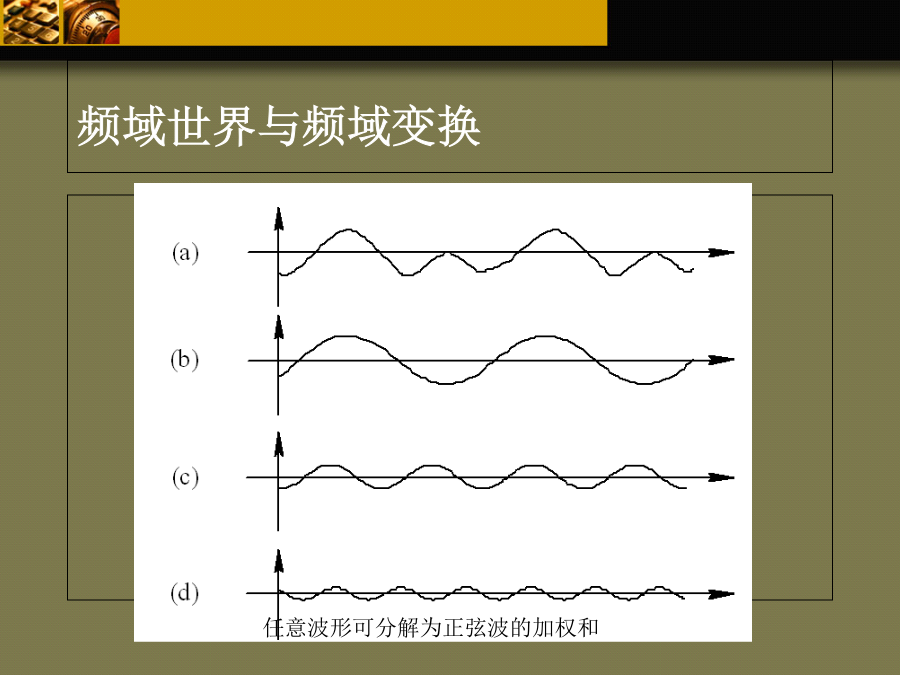
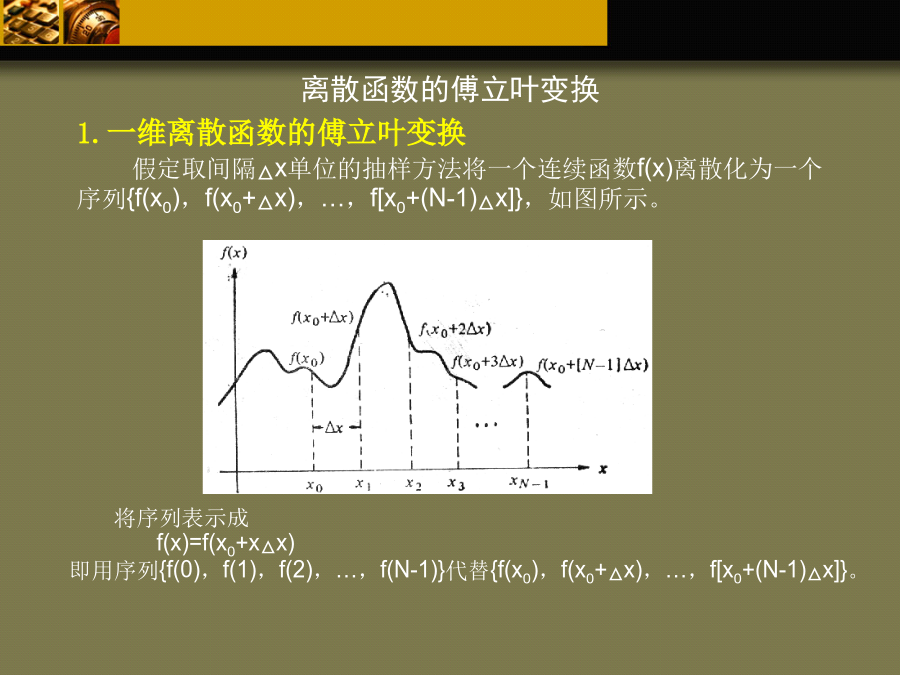
图像变换频域世界与频域变换傅立叶变换
连续函数的傅立叶变换
1.一维连续函数的傅立叶变换
令f(x)为实变量x的连续函数，f(x)的傅立叶变换用F(u)表示，则定义式为

若已知F(u)，则傅立叶反变换为

这里f(x)是实函数，它的傅立叶变换F(u)通常是复函数。F(u)的实部、虚部、振幅、能量和相位分别表示如下：

2.二维连续函数的傅立叶变换
傅立叶变换很容易推广到二维的情况。如果f(x，y)是连续和可积的，且F(u，v)是可积的，则二维傅立叶变换对为离散函数的傅立叶变换
1.一维离散函数的傅立叶变换
假定取间隔△x单位的抽样方法将一个连续函数f(x)离散化为一个序列{f(x0)，f(x0+△x)，…，f[x0+(N-1)△x]}，如图所示。
被抽样函数的离散傅立叶变换定义式为

F(u)=

式中u=0，1，2，…，N﹣1。反变换为

f(x)=

式中x=0，1，2，…，N-1。
例如：对一维信号f(x)=[1010]进行傅立叶变换。
由

得u=0时，

u=1时,u=2时,

u=3时,

在N=4时，傅立叶变换以矩阵形式表示为

F(u)==Af(x)2.二维离散函数的傅立叶变换
在二维离散的情况下，傅立叶变换对表示为
F(u，v)=

式中u=0，1，2，…，M-1；v=0，1，2，…，N-1。
f(x，y)=

式中x=0，1，2，…，M-1；y=0，1，2，…，N-1。

一维和二维离散函数的傅立叶谱、相位和能量谱也分别由前面式子给出，唯一的差别在于独立变量是离散的。
一般来说，对一幅图像进行傅立叶变换运算量很大，不直接利用以上公式计算。现在都采用傅立叶变换快速算法，这样可大大减少计算量。为提高傅立叶变换算法的速度，从软件角度来讲，要不断改进算法；另一种途径为硬件化，它不但体积小且速度快。原图二维离散傅立叶变换的性质再将F(x,v)沿每一列进行一次一维傅立叶变换，就可得二维傅立叶变换F(u,v)，即显然，改为先沿列后沿行分离为两个一维变换，其结果是一样的。即若f(x,y)←→F(u,v)，则

4)周期性和共轭对称性5）旋转不变性傅立叶变换的旋转性8）微分性质6）分配性和比例性7）平均值9）卷积定理设