
信号与系统傅里叶变幻.ppt

yy****24





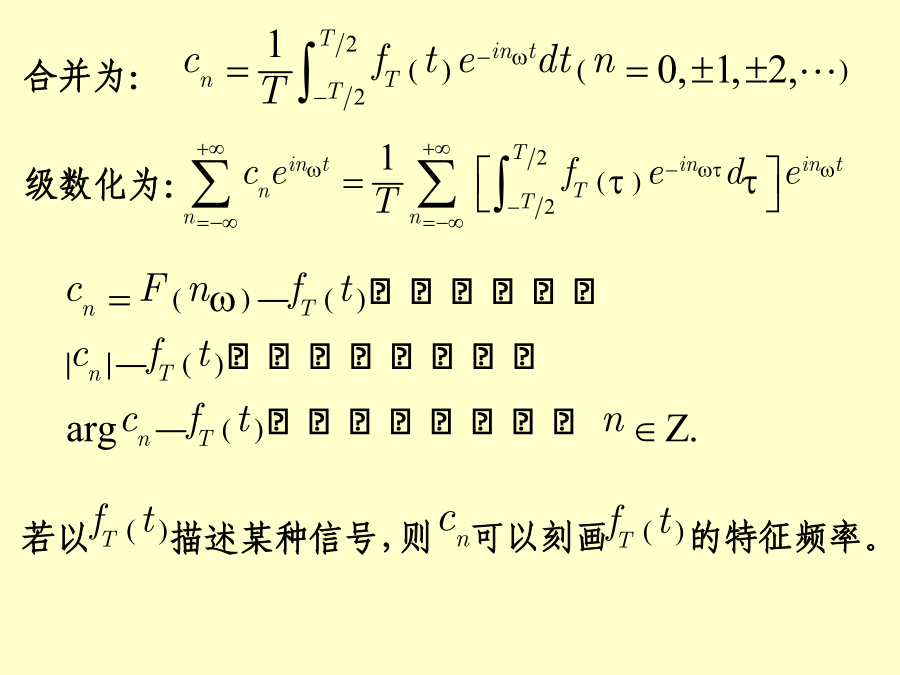


亲,该文档总共57页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

信号与系统傅里叶变幻.ppt
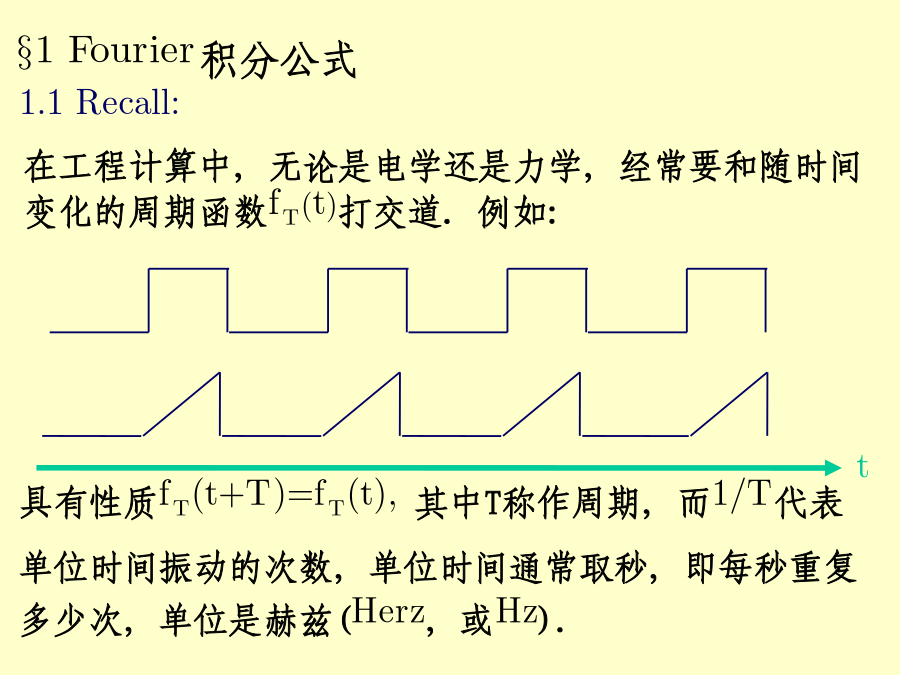
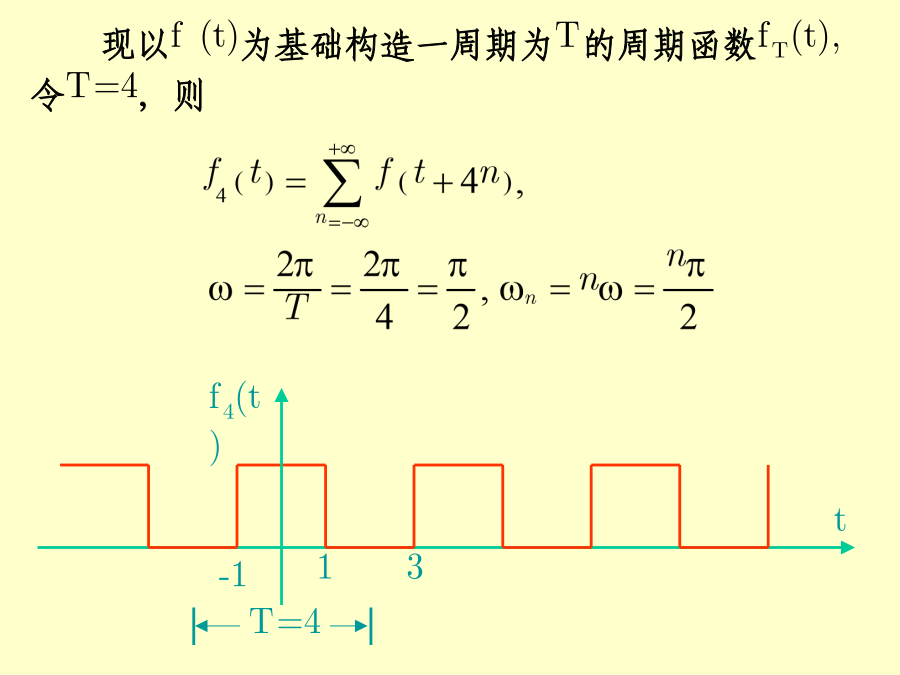
积分变换§1Fourier积分公式最常用的一种周期函数是三角函数。人们发现,所有的工程中使用的周期函数都可以用一系列的三角函数的线性组合来逼近.——Fourier级数研究周期函数实际上只须研究其中的一个周期内的情况即可,通常研究在闭区间[-T/2,T/2]内函数变化的情况.引进复数形式:级数化为:合并为:对任何一个非周期函数f(t)都可以看成是由某个周期函数fT(t)当T时转化而来的.作周期为T的函数fT(t),使其在[-T/2,T/2]之内等于f(t),在[-T/2,T/2]之外按周期T延拓到整个数

信号与系统周期信号傅里叶级数.ppt
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

连续信号的傅里叶分析.pptx
第3章连续信号旳傅里叶分析齐开悦博士上海交通大学电子工程系要点内容:连续时间周期信号旳傅里叶级数连续时间傅立叶变换;傅立叶级数与傅立叶变换之间旳关系;傅立叶变换旳性质;系统旳频率响应及系统旳频域分析;采样(抽样)及采样(抽样)定理;3.1引言Introduction1768年生于法国1823年提出“任何周期信号都能够用正弦函数旳级数来表达”拉格朗日反对刊登1823年首次刊登“热旳分析理论”1829年狄里赫利第一种给出收敛条件傅里叶旳两个最主要旳贡献——FourierSeriesRepresentation

信号的产生及傅里叶分析.docx
实验名称:信号的产生及傅里叶分析二、实验目的:1、熟悉MATLAB环境2、产生几种常用的信号3、对信号用DFT做频谱分析三、实验过程:1、编程实现几种常用序列,正弦序列、矩形序列、指数序列的产生。2、编程实现序列的离散傅里叶变换(DFT),输入X(n),输出X(K)3、对于正弦序列、矩形序列、指数序列做DFT,画出频谱图。4、调用FFT函数,对正弦序列、矩形序列、指数序列做变换,画出频谱图。四、实验结果:1、正弦序列及其dft变换的频谱图:2、矩形序列及其DFT变换的频谱图:3、指数序列及其DFT变换的频

信号与系统第7讲-傅里叶级数的性质与收敛问题.ppt
第七讲傅里叶级数的性质与收敛问题内容提要内容提要线性性质时移性质时间反转性质时域尺度变换性质相乘性质周期卷积性质周期卷积性质周期卷积性质共轭对称性共轭对称性帕斯瓦尔定理举例1举例2内容提要傅里叶级数的收敛性傅里叶级数的收敛条件几个不满足狄里赫利条件的信号几个不满足狄里赫利条件的信号几个不满足狄里赫利条件的信号关于傅里叶级数收敛性的几点说明最小均方误差近似最小均方误差近似吉伯斯现象吉伯斯现象内容提要系统函数与频率响应利用傅里叶级数求LTI系统的输出谢谢大家!
