灰色动态模型及其在人口预测中的应用.pdf

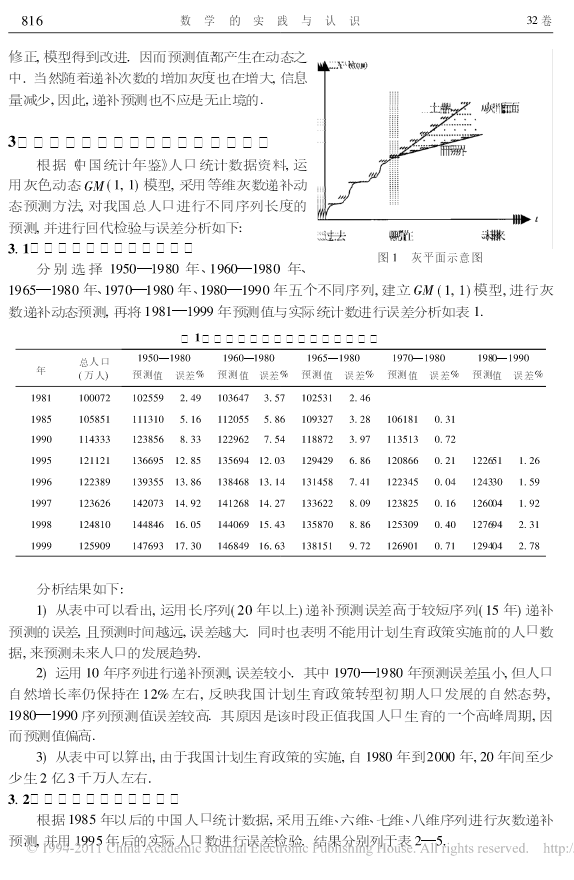
第32卷第5期数学的实践与认识Vol.32No.5
2002年9月MATHEMATICSINPRACTICEANDTHEORYSep.,2002

灰色动态模型及其在人口预测中的应用

郝永红1,王学萌2

(1.山西大学环境与资源学院,太原030006)
(2.山西省农业科学院农业资源综合考察所,太原030006)

摘要:一个国家人口的数量直接影响着其经济、社会的发展和资源的利用,中国是世界上人口的第一大
国,人口问题一直是制约中国发展的第一因素.本文应用灰色系统等维灰数递补动态预测模型,对中国未来
50年的人口数量进行了动态预测,通过检验表明,该模型合理、方法简便可行、结果符合实际,为中国经济和
社会发展的决策和研究提供了科学依据.
关键词:等维灰数递补动态预测;人口预测;可持续发展

1前言
一个国家人口的数量直接影响着其经济、社会的发展和资源的利用.中国是世界上人
口的第一大国,人口问题一直是制约中国发展的第一因素,因此,在21世纪到来之际,预测
中国未来50年人口数量及其增长率,有着重要的现实意义.
本文根据灰色系统等维灰数递补动态预测模型对未来50年中国的人口数量进行了动
态预测.通过实证分析,对模型进行了检验,预测误差小,应用效果比较符合实际.

2灰色预测原理、模型和方法
2.1灰色预测概念
灰色预测的特点是单数列预测.在形式上,只运用预测对象自身的时间序列建立模型,
与其相关联的因素没有参与运算和建模.这是否说,那些因素对预测对象没有影响和作用
呢?模型是否不够全面或完善呢?并不是,灰色系统的“灰”,正体现在这里.任何一个客观系
统,究竟含有多少因素,是难以说清楚的.如人口系统,影响其增长的因素既有社会经济的,
也有自然环境的,还有科学技术方面的,这些众多的因素,不是用几个指标所能表达清楚的.
而且,这些因素之间的结构关系难以准确描述,它们对人口增长的作用更是无法精确计算.
多数因素都在动态变化之中,其运行机制和变化规律难以完全明白.这反映了人口系统具
有明显的灰色性,他是一个既含有许多已知信息,又存在许多未知或未确知信息的灰色系
统.灰色系统理论把这样受众多因素影响,而又无法确定其复杂关系的量,称为灰色量.对
灰色量进行预测,不必拼凑数据不准,关系不清、变化不明的参数,而是从自身的时间序列中
寻找有用信息建立模型,发现和认识内在规律,并进行预测.但不是说,像人口这样的灰色
量不受任何因素的影响,而是说,他们时间序列数据的动态变化,正是那些主要的、次要的,
直接的、间接的,已知的、未知的,明显的、隐含的众多因素相互联系、相互制约协同作用的结

收稿日期:2002-03-01
基金项目:山西省青年科技研究基金项目;太原市科技启明星计划项目(20021028)
814数学的实践与认识32卷

果.实际上它们的影响,已或多或少地反映在起伏波动的数据里.如每年的总人口数,既有
育龄妇女当年生育的因素,也受育龄妇女没有生育的影响,既有老人自然死亡的因素,也有
疾病、事故、自然灾害等的影响,既有国家计划生育政策的积极作用,也受传统思想的影响
等.正是这些既明白又不完全清楚的众多因素共同作用的结果,才获得现实的一个灰色量
——总人口数.
灰色预测的另一特点是不追求大样本量.灰色系统分析有个重要原则就是现实信息优
先的原则,即在处理历史信息和现实信息的关系时,重视现实信息.这是由于在信息不完全
系统中,表征或反映它的状态特征和行为的主要是现实信息,直接影响系统未来发展趋势、
起着主导作用的也是现实信息;同时在历史信息中,能反映客观事物发展规律的那部分信
息,都会以这样或那样的方式被现实信息所载有.这一点对于社会、经济等本征性灰色系统
更为明显.显然,我们不能用改革开放前的社会经济信息来描述和表征改革开放后的社会
经济状态,更不能将它作为主要依据来预测未来社会经济的发展趋势.所以,灰色预测不追
求大量历史数据,也不荷求它的典型分布.而是对已掌握的部分信息进行合理的技术处理,
通过建立模型,在更高的层次上,对系统动态过程进行科学的描述.
2.2灰色预测模型的动态特征
灰色单数列预测,与数理统计学中的时间序列预测,有本质的不同.时间序列预测是利
用时间序列的几何特征和统计规律进行预测.是一种历史的和静态的研究.而灰色数列预
测是一种现实的和动态的分析与预测.这是由于灰色动态模型不是利用时间序数据直接建
模,而是将序列数据作一次累加生成后,再建立微分方程.下面通过对灰色动态模型GM
(1,1)进行分析与讨论,来说明这个特征.
GM(1,1)模型为一阶微分方程:
(1)
dx(t)(1)
+ax(t)=u(1)
dt
方程中的X(1)(t)为原始数据序列X(0)(t)的依次累加值,即系统的逐年累计总量;而方
程左边第一项为系统的逐