应力状态的概念学习教案.ppt

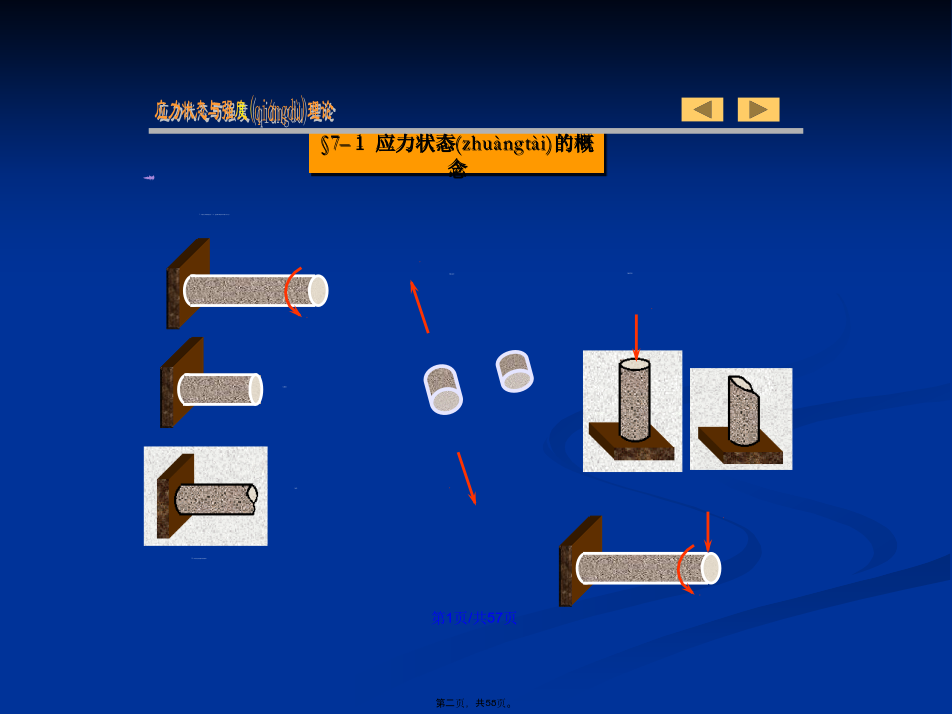
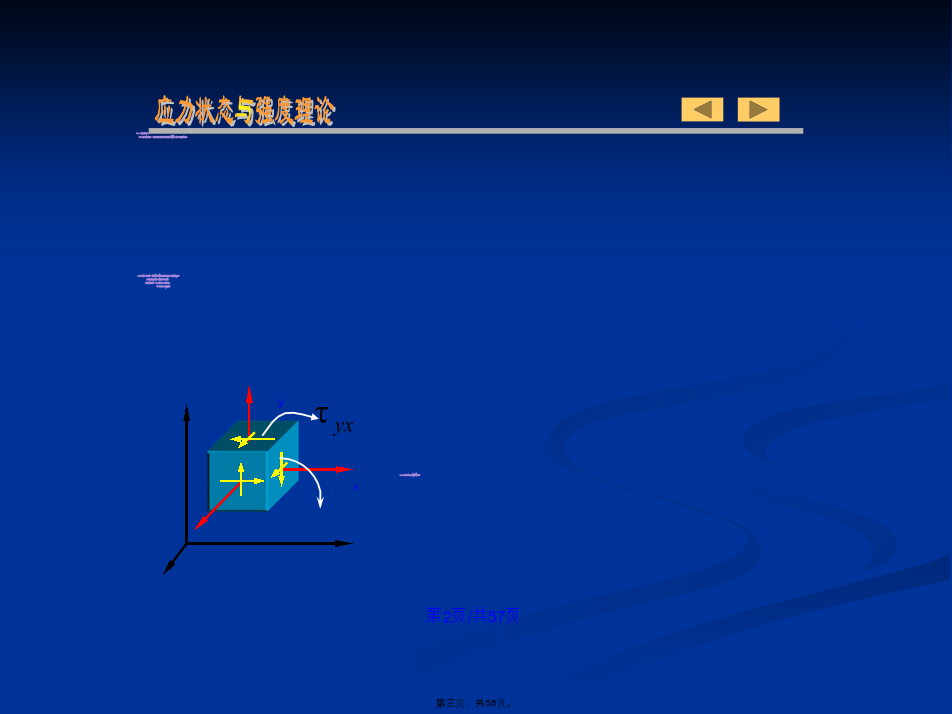
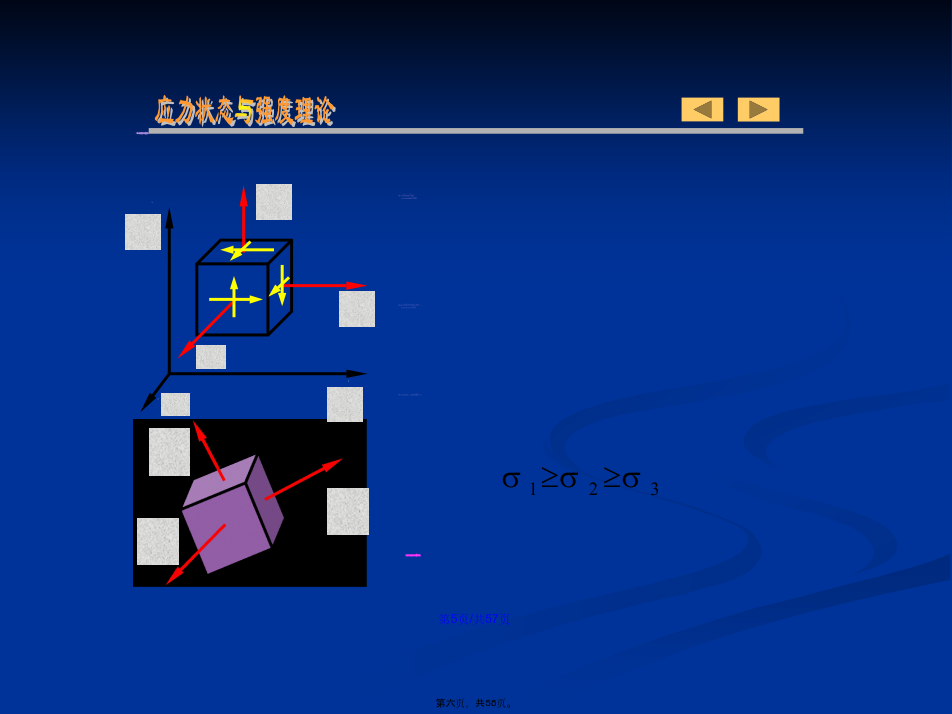
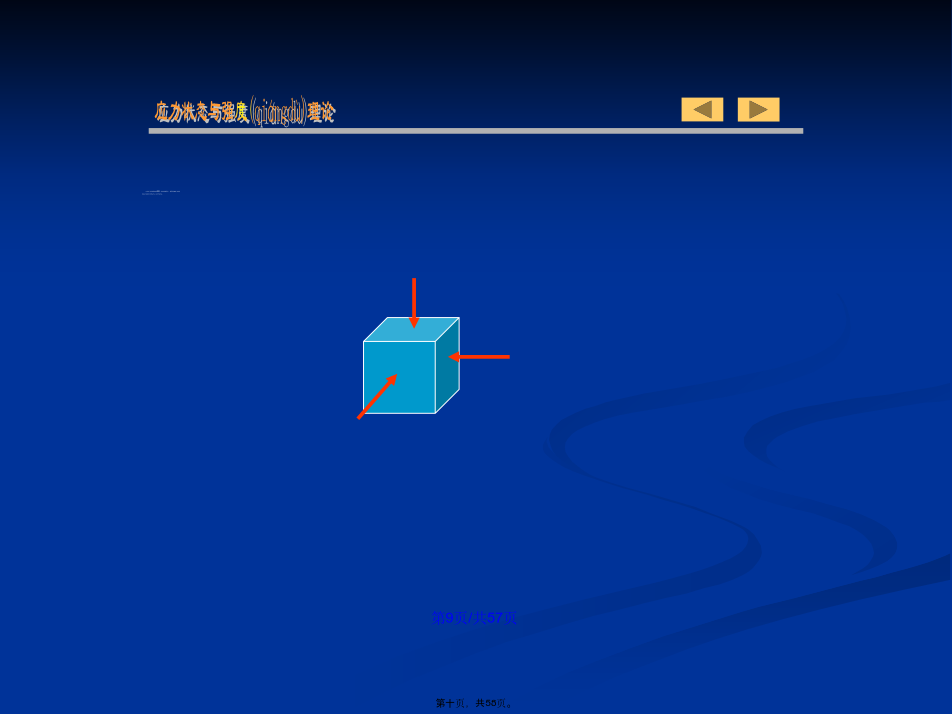
会计学§7–１应力状态(zhuàngtài)的概念应力状态与强度(qiángdù)理论七、主平面、主应力：单向应力状态（UnidirectionalStateofStress）：
一个(yīɡè)主应力不为零的应力状态。§7–2二向和三向应力(yìnglì)状态的实例y三向应力状态的实例(shílì)：在滚珠轴承中，轴承外圈在与滚珠
接触点处的应力状态为三向应力状态，§7–3二向应力状态(zhuàngtài)分析——解析法正应力以拉应力为正，压应力为负；
剪应力对单元体内任意点的矩为顺时针转向(zhuǎnxiàng)时为正，反之为负；
由轴逆时针转过角为正，反之为负。考虑切应力互等和三角(sānjiǎo)变换，得：应力状态(zhuàngtài)与强度理论二、主应力、主平面二、主应力、主平面例2、求图示单元体的主应力及主平面(píngmiàn)，在单元体上画出主
平面(píngmiàn)和主应力。应力状态与强度(qiángdù)理论铸铁圆轴扭转破坏(pòhuài)现象分析四、两个(liǎnɡɡè)互相垂直截面上应力的关系§7–4平面(píngmiàn)应力状态分析——图解法上式中皆为已知量，故此方程是以和
为变量的圆周方程，这一圆称为应力(yìnglì)圆（或莫尔圆），由
德国工程师OttoMohr提出。
由公式可见，在—直角坐标系中，应力(yìnglì)圆具有
以下特征：
（1）圆心坐标为—圆心必在坐标轴上
（2）半径为
（3）应力圆圆周上任一点的纵、横坐标，分别代表
单元体中某一相应(xiāngyīng)斜截面上的和，因此应力圆圆
周上所有各点的坐标就表达了一点的应力状态。建立应力坐标系，如下(rúxià)图所示，
（注意选好比例尺）sx四、在应力(yìnglì)圆上标出极值应力(yìnglì)解法2—解析法：分析(fēnxī)——建立坐标系如图课堂练习：
1、画出单向拉伸(lāshēn)、单向压缩应力状态的应力圆。2、画出纯剪切应力状态(zhuàngtài)的应力圆。2、三向应力(yìnglì)状态分析§7–6广义(guǎngyì)胡克定律三、复杂应力状态下的应力---应变(yìngbiàn)关系主应力---主应变(yìngbiàn)关系五、体积应变(yìngbiàn)与应力分量间的关系例5已知一受力构件(gòujiàn)自由表面上某一点处在表面内的主应变分别为：1=24010-6，3=–16010-6，弹性模量E=210GPa，泊松比为=0.3，试求该点处的主应力及另一主应变。§7－7复杂应力(yìnglì)状态下的应变能密度应力状态(zhuàngtài)与强度理论应力(yìnglì)状态与强度理论例6证明三个弹性常数(chángshù)间的关系。一、引子(yǐnzi)：二、强度理论：是关于(guānyú)“构件发生强度失效（failurebylost
strength）起因”的假说。三、四个常用(chánꞬyònꞬ)强度理论2、最大伸长线应变（第二强度）理论(lǐlùn)：
认为构件的断裂是由最大拉应力引起的。当最大伸长线应变达到材料单向拉伸试验下的极限应变时，构件就断了。3、最大切应力（第三强度）理论：
认为构件的屈服(qūfú)是由最大切应力引起的。当最大切应力达到单向拉伸试验的极限切应力时，构件就屈服(qūfú)了。4、畸变能密度理论（第四强度）理论：
认为构件的屈服(qūfú)是由畸变能密度引起的。当畸变能密度达到单向拉伸试验屈服(qūfú)时的畸变能密度时，构件就屈服(qūfú)了。应力状态与强度(qiángdù)理论四、强度理论(lǐlùn)的应用（二）强度理论的选用原则(yuánzé)：依破坏形式而定。解：危险点A的应力(yìnglì)状态如图：例2薄壁圆筒受最大内压时,测得x=1.8810-4,y=7.3710-4,已知钢的E=210GPa，[]=170MPa,泊松比=0.3，试用(shìyòng)第三强度理论校核其强度。本章(běnzhānꞬ)结束内容(nèiróng)总结