
spss多元线性回归.docx

王子****青蛙








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
spss多元线性回归.pdf
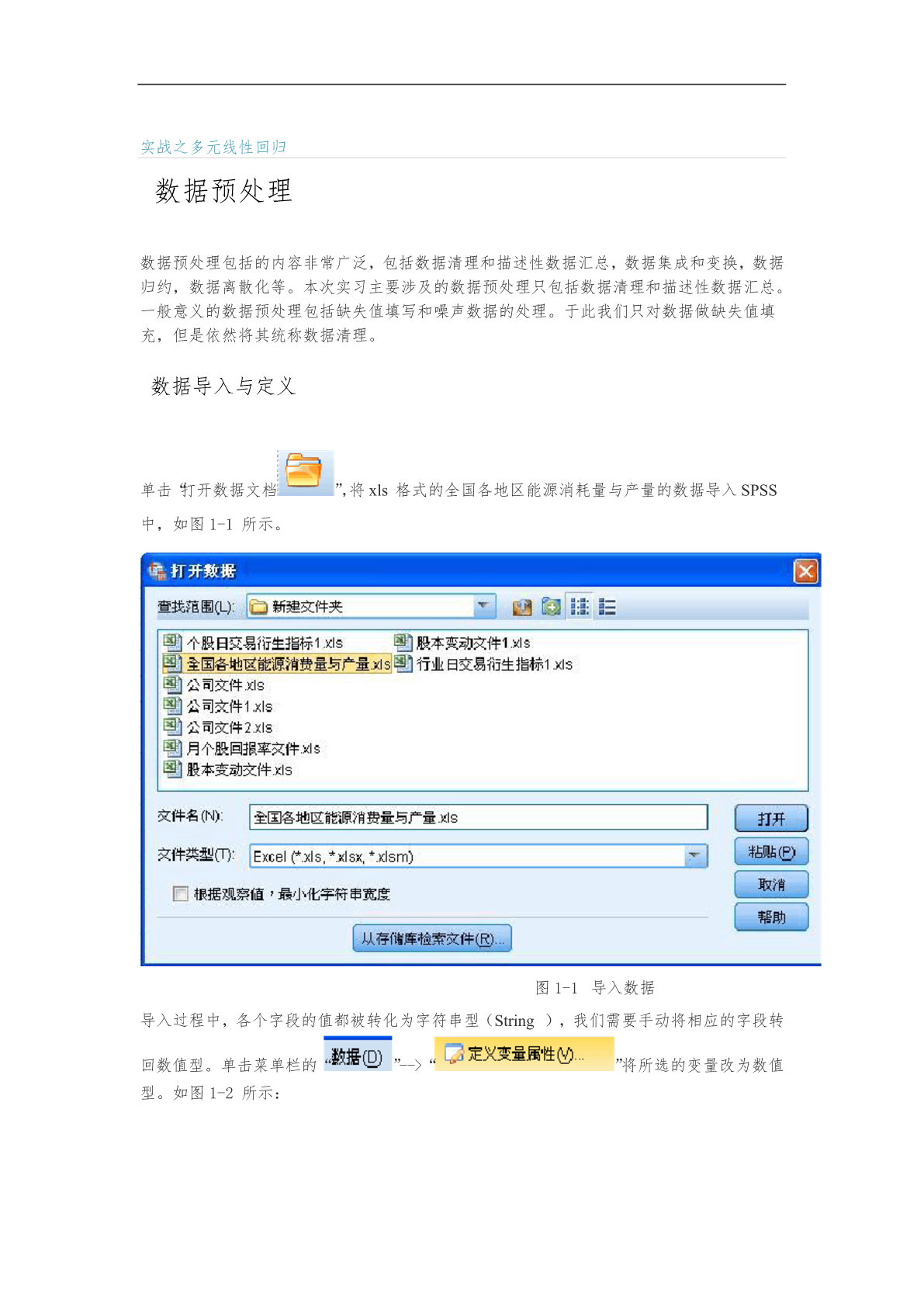
实战之多元线性回归数据预处理数据预处理包括的内容非常广泛,包括数据清理和描述性数据汇总,数据集成和变换,数据归约,数据离散化等。本次实习主要涉及的数据预处理只包括数据清理和描述性数据汇总。一般意义的数据预处理包括缺失值填写和噪声数据的处理。于此我们只对数据做缺失值填充,但是依然将其统称数据清理。数据导入与定义单击“打开数据文档”,将xls格式的全国各地区能源消耗量与产量的数据导入SPSS中,如图1-1所示。图1-1导入数据导入过程中,各个字段的值都被转化为字符串型(String),我们需要手动将相应的字段

spss多元线性回归.docx
1.1数据预处理数据预处理包括的内容非常广泛,包括数据清理和描述性数据汇总,数据集成和变换,数据归约,数据离散化等。本次实习主要涉及的数据预处理只包括数据清理和描述性数据汇总。一般意义的数据预处理包括缺失值填写和噪声数据的处理。于此我们只对数据做缺失值填充,但是依然将其统称数据清理。1.1.1数据导入与定义单击“打开数据文档”,将xls格式的全国各地区能源消耗量与产量的数据导入SPSS中,如图1-1所示。图1-1导入数据导入过程中,各个字段的值都被转化为字符串型(String),我们需要手动将相应的字段转

SPSS多元线性回归.pdf
SPSS多元线性回归分析实例操作步骤-spss做多元线性回归.pdf
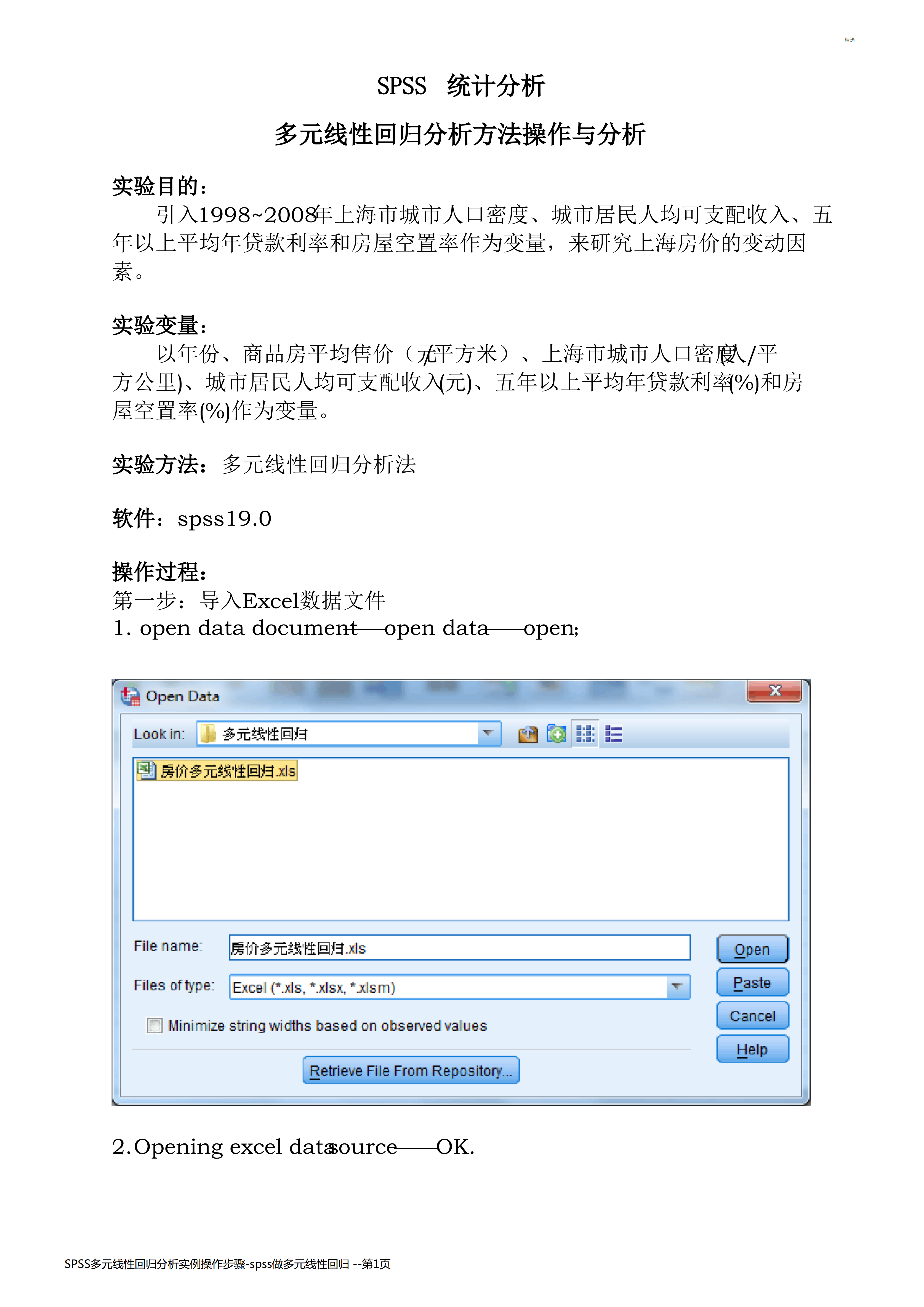
SPSS多元线性回归分析实例操作步骤-spss做多元线性回归--精选SPSS统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Exc
SPSS多元线性回归分析实例操作步骤-spss做多元线性回归.pdf
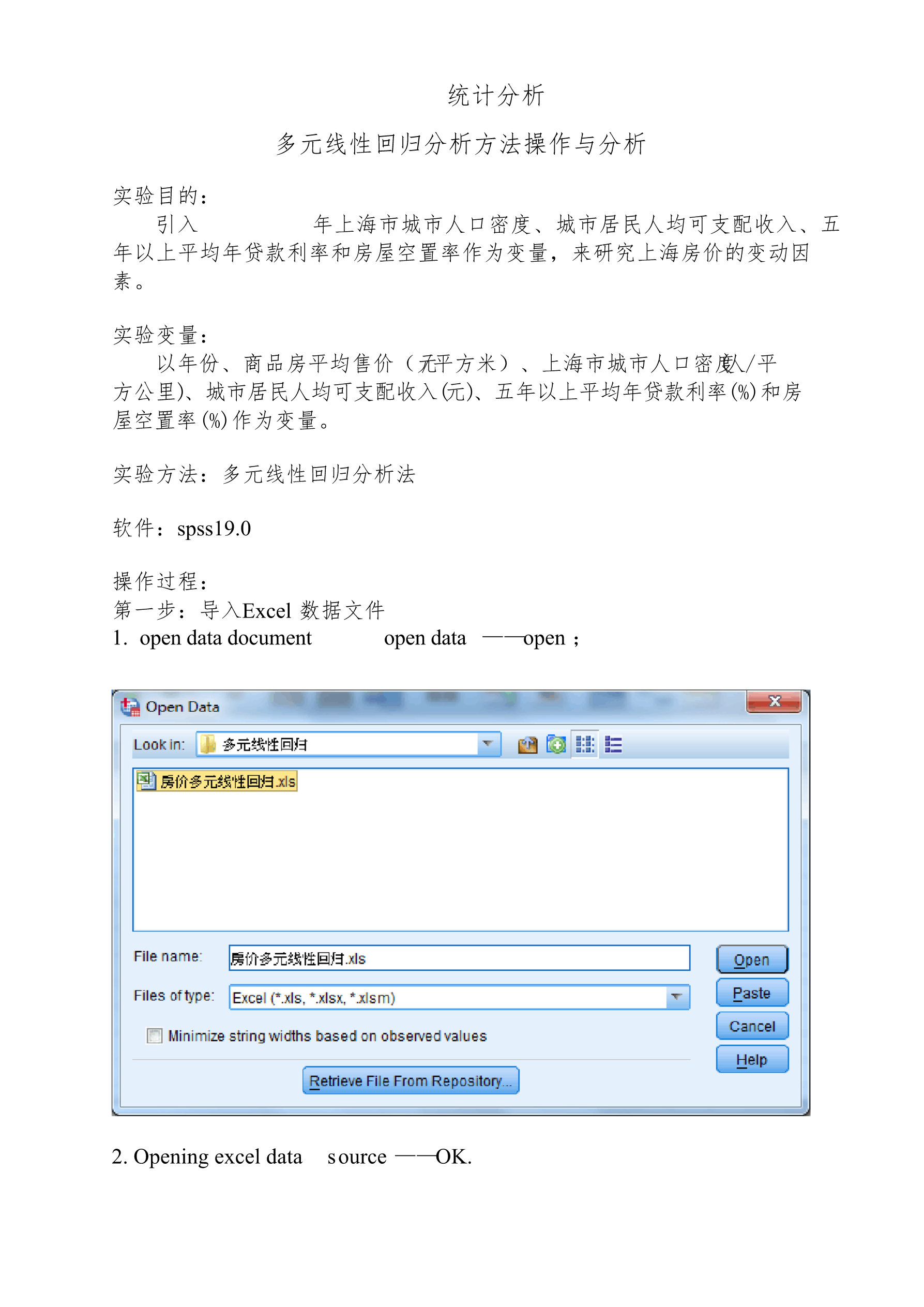
统计分析多元线性回归分析方法操作与分析实验目的:引入年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.opendatadocumentopendata——open;2.Openin
