
选考部分备选练习.doc

as****16










亲,该文档总共14页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

选考部分备选练习.doc
选考部分备选练习本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(2010·湖南六校)如图,在平行四边形ABCD中,E为CD上一点,DEEC=23,连结AE,BE,BD,且AE,BD交于点F,则S△DEFS△EBFS△ABF=()A.41025B.4925C.235D.2525[答案]A[解析]由题意可知,三角

浙江选考物理部分.docx
2018年4月浙江省普通高校招生选考科目考试选择题I(本题共13小题,每小题3分,共39分.每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.通过理想斜面实验得出“力不是维持物体运动的原因”的科学家是()A.亚里士多德B.伽利略C.笛卡尔D.牛顿2.某驾驶员使用定速巡航,在高速公路上以时速110公里行驶了200公里。其中“时速110公里”、“行驶200公里”分别是指()A.速度、位移B.速度、路程C.速率、位移D.速率、路程3.用国际单位制的基本单位表示能量的单位,下列正确的
备选方案比选.pptx
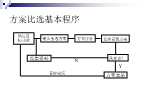
方案比选基本程序互斥型——互斥方案指若干个方案最多只能选一个,选择其中的一个方案将意味着自动放弃其它方案。独立型——独立方案是指方案的采纳与否只受自身条件的限制,与其它方案的取舍无关。混合型——混合方案是指在一组方案中,既有互斥型方案,又有独立型方案。一、互斥方案的比选现有X、Y两个互斥方案,寿命相同,现金流量及指标计算结果如表所示,试评价选择方案(i0=12%)。差额净现值法、差额内部收益率法:增量分析法(incrementalanalysis)通过计算增量净现金流量评价增量投资经济效果。步骤:(1)将

选考部分 选考3 中外历史人物评说.ppt
谢谢

选考部分 选考3 中外历史人物评说.doc
[真题演练]1.(2019·高考全国卷Ⅰ)阅读材料回答问题。材料公元前544年吴国公子季札出使鲁、郑、卫、晋等中原诸国。季札对于各国贵族视为“文明”象征的乐舞与歌诗皆能一一点评得其精髓;对于各国政治现状他也能作出准确的研判。各国原本视江南为蛮荒之地为“文身断发”的“夷人”聚居之处季札的到来让他们眼界一开。季札出使途经徐国知道徐国国君对他的佩剑十分喜爱只因要出访他国未能相赠。季札返回途中至徐徐君已死他解下佩剑挂在徐君墓前的树上。随从认为这样做没有意义季札说我当初知道徐君喜爱我这把剑“始吾心已许
