
素材-全国-2019_六年级数学下册 一 比例 1《比例的意义与基本性质》练一练一教材分析 浙教版.doc

春岚****23



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

素材-全国-2019_六年级数学下册 一 比例 1《比例的意义与基本性质》练一练一教材分析 浙教版.doc
2《练一练一》教材分析巩固学生对比例意义与性质的认知,帮助他们从“比例”的角度去分析和解决问题。第1题,(1)分别写出第一次和第二次参加人数与租用旅游车数量的比,即320:8(40:1)与960:24(40:1),然后判断这两个比能否组成比例。判断时,可以根据比例的意义,看比值是否相等;也可以先假设两个比能组成比例,设320:8=960:24,然后看内项积是否等于外项积,320×24=960×8,因此假设成立,这两个比能组成比例。用同样方法完成第(2)题。根据班级情况,可以追问:这里的比值

六年级数学下册 一 比例 1《比例的意义与基本性质》练一练一教材分析 浙教版 素材.doc
《练一练一》教材分析巩固学生对比例意义与性质的认知,帮助他们从“比例”的角度去分析和解决问题。第1题,(1)分别写出第一次和第二次参加人数与租用旅游车数量的比,即320:8(40:1)与960:24(40:1),然后判断这两个比能否组成比例。判断时,可以根据比例的意义,看比值是否相等;也可以先假设两个比能组成比例,设320:8=960:24,然后看内项积是否等于外项积,320×24=960×8,因此假设成立,这两个比能组成比例。用同样方法完成第(2)题。根据班级情况,可以追问:这里的比值表示什么意思?直观

六年级数学下册 一 比例 1《比例的意义与基本性质》练一练一教材分析 浙教版.doc
3《练一练一》教材分析巩固学生对比例意义与性质的认知,帮助他们从“比例”的角度去分析和解决问题。第1题,(1)分别写出第一次和第二次参加人数与租用旅游车数量的比,即320:8(40:1)与960:24(40:1),然后判断这两个比能否组成比例。判断时,可以根据比例的意义,看比值是否相等;也可以先假设两个比能组成比例,设320:8=960:24,然后看内项积是否等于外项积,320×24=960×8,因此假设成立,这两个比能组成比例。用同样方法完成第(2)题。根据班级情况,可以追问:这里的比值表示什么意思?直

素材-全国-2019_六年级数学下册 一 比例 1《比例的意义与基本性质》教材分析 浙教版.doc
3《比例的意义与性质》教材分析比例的意义是建立在“比”和“比相等”概念的基础上的。看与问教材首先提供了两组数据,即森林的面积与供氧量、物体的高度与影长,要求学生写出相应的比,并求出比值,然后把比值相等的两个比用等号连接,告诉学生这个等式就是“比例”。需要时可以进一步追问学生:什么是比例?它与比有什么联系与区别?强调比例是表示两个比之间相等关系的一个式子。做与说第一环节,请学生再写几个比例式,并加以判别,强化比例的意义。然后介绍比例的内项和外项,以及比例的书写格式和规范读法。第
素材-全国-2019_六年级数学下册 一 比例 1《比例的意义与基本性质》比例(主题图)教材分析 浙教版.doc
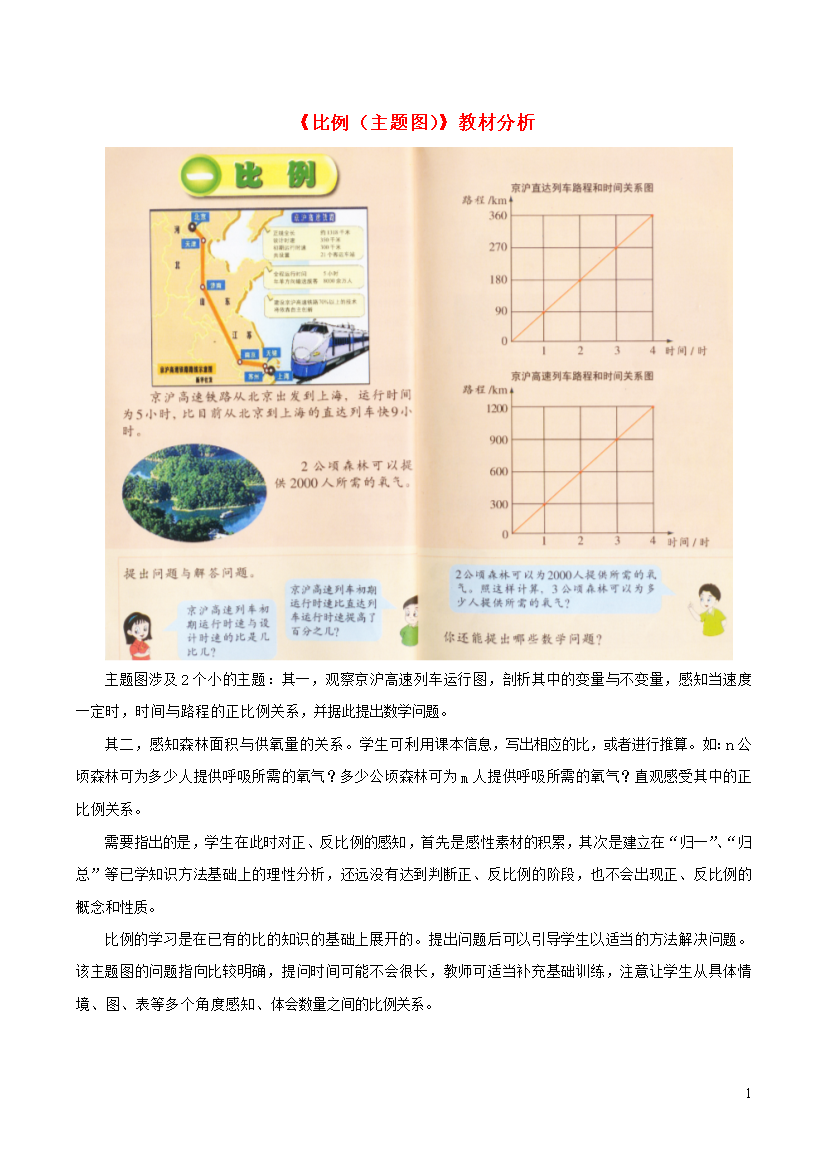
1《比例(主题图)》教材分析主题图涉及2个小的主题:其一,观察京沪高速列车运行图,剖析其中的变量与不变量,感知当速度一定时,时间与路程的正比例关系,并据此提出数学问题。其二,感知森林面积与供氧量的关系。学生可利用课本信息,写出相应的比,或者进行推算。如:n公顷森林可为多少人提供呼吸所需的氧气?多少公顷森林可为m人提供呼吸所需的氧气?直观感受其中的正比例关系。需要指出的是,学生在此时对正、反比例的感知,首先是感性素材的积累,其次是建立在“归一”、“归总”等已学知识方法基础上的理性分析,还
