半参数回归模型中参数随机加权估计的大样本性质_吴耀华.pdf

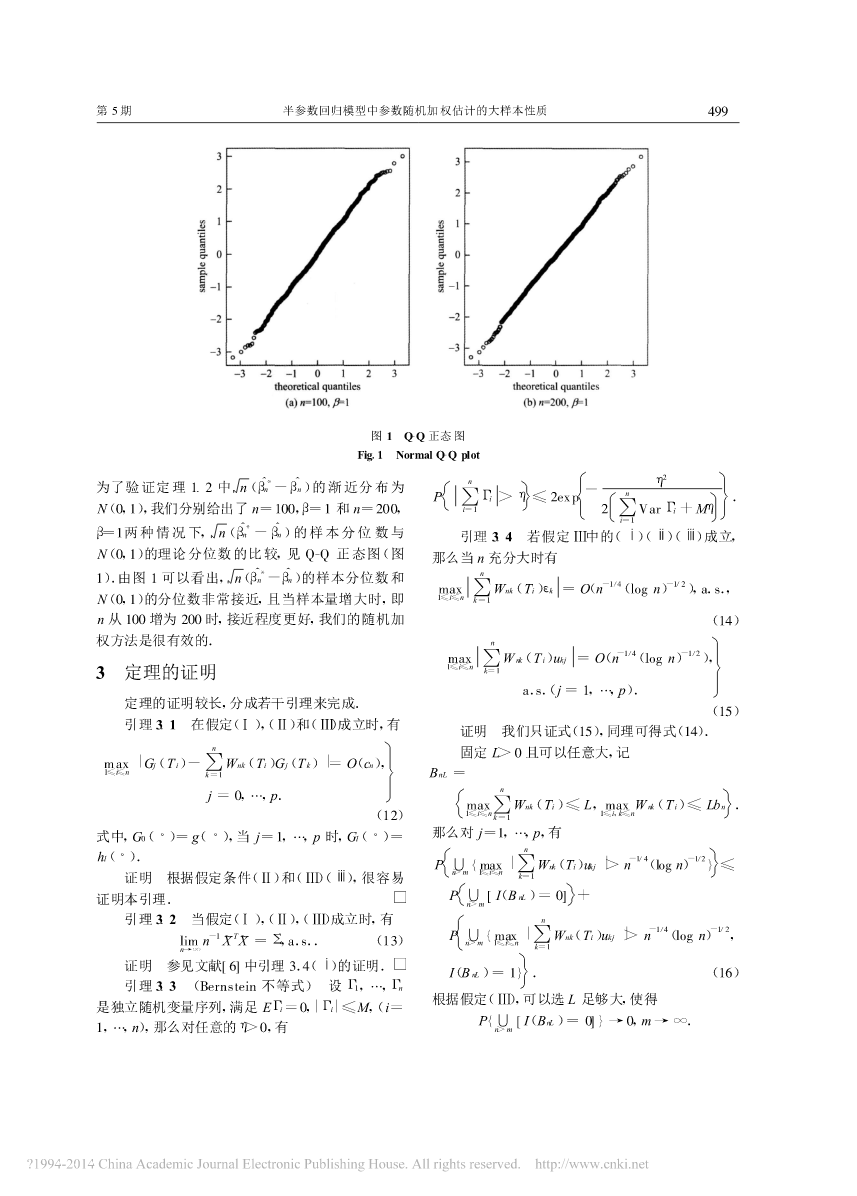
第38卷第5期Vol.38,No.5
2008年5月JOURNALOFUNIVERSITYOFSCIENCEANDTECHNOLOGYOFCHINAMay2008

文章编号:0253-2778(2008)05-0496-09

半参数回归模型中参数随机加权估计的大样本性质

吴耀华,刘常胜,王占锋

(中国科学技术大学统计与金融系,安徽合肥230026)

摘要:主要考虑了同方差型的半参数线性回归模型中参数的随机加权最小二乘估计(RWLSE).讨
论了用随机加权Bootstrap方法来逼近LSE的分布,证明这种逼近是以概率1渐近有效的.
关键词:半参数回归模型;渐近正态性;随机加权最小二乘估计
中图分类号:O212.7文献标识码:A
AMSSubjectClassification(2000):Primary62J12;Secondary62F40

Largesamplepropertiesofrandomweightedestimatorsforparametric
componentinsemi-parametricregressionmodels

WUYao-hua,LIUChang-sheng,WANGZhan-feng

(DepartmentofStatisticsandFinance,UniversityofScienceandTechnologyofChina,Hefei230026,China)

Abstract:Therandomlyweightedleastsquareestimator(RWLSE)fortheparametriccomponentinsemi-
parametricregressionmodelswasmainlydiscussed.Therandomlyweightedbootstrapmethodwasusedto
approximatethedistributionoftheleastsquareestimators(LSE),anditwasdemonstratedthatthe
approximationisasymptoticlyvalidwithprobabilityone.
Keywords:semi-parametricregressionmodels;asymptoticnormalityproperties;randomlyweightedleast
squareestimator

的研究成果,文献[8]对此进行了一个总结.例如在
0引言
随机设计点下有
L
考虑如下半参数回归模型:2-1
n(βn-β)N(0,σ΢).
T
Yi=Xiβ+g(Ti)+εi,i=1,…,n.(1)222
式中,σ=Eε1,΢=Cov(X1-E(X1T1)),当σ和΢
T
式中,Xi=(Xi1,…,Xip);(Xi,Ti)是i.i.d.的随机未知时,虽然可以用样本来估计σ2和΢,但当样本
T
设计点;β=(β1,…,βp)是未知的p维参数向量;量较小时估计值不是很精确,若用此估计值来做β
22
ε1,…,εn是i.i.d.随机误差;Eε1=0,Eε1=σ,且的假设检验或构造β的置信区间,效率比较低.从应

(Xi,Ti)与εi独立.用的角度看,研究n(βn-β)的分布逼近问题尤为
关于上述模型的研究,自文献[1]在研究气候条重要.
件对电力需求影响的关系这一实际问题时提出上述文献[2]详细论述了在固定设计点下对于异方
模型以来,半参数回归模型的研究越来越受到很大差半参数回归模型广义最小二乘估计(GLSE)的分
的重视.单就参数部分的估计与渐近性质就有大量布逼近问题,并证明了上述逼近是依概率渐近有效

收稿日期:2006-11-21;修回日期:2007-04-03
基金项目:国家自然科学基金(10471136)和中国科学院知识创新重要方向项目(KJCX3-SYW-S02)资助.
作者简介:吴耀华(通讯作者),男,1963年生,博士/教授.研究方向:大样本理论,线性模型,非参数统计.E-mail:[e-mail]
第5期半参数回归模型中参数随机加权估计的大样本性质497

的.本文将对同方差随机设计点模型,构造未知参数j=1,…,p,本文需要如下假定:
4
＊假定(Ⅰ)supE(‖X1‖T=t)<∞和΢=
β的随机加权最小二乘估计(RWLSE)βn,并证明了0≤t≤1

＊Cov{X1-E(X1T1)}是一个正定阵,随机误差εi与
用n(βn-βn)的分布逼近n(βn-β)的分布是以概
ii独立
率1渐近有效的,该结果可以用于构造β的大样本(X,T).
假定(Ⅱ)g(·)和hj(·)都是一阶Lipschitz
置信区间和进行假设检验.
连续函数
下面我们考虑由