关于灰色模型的累加生成效果.pdf

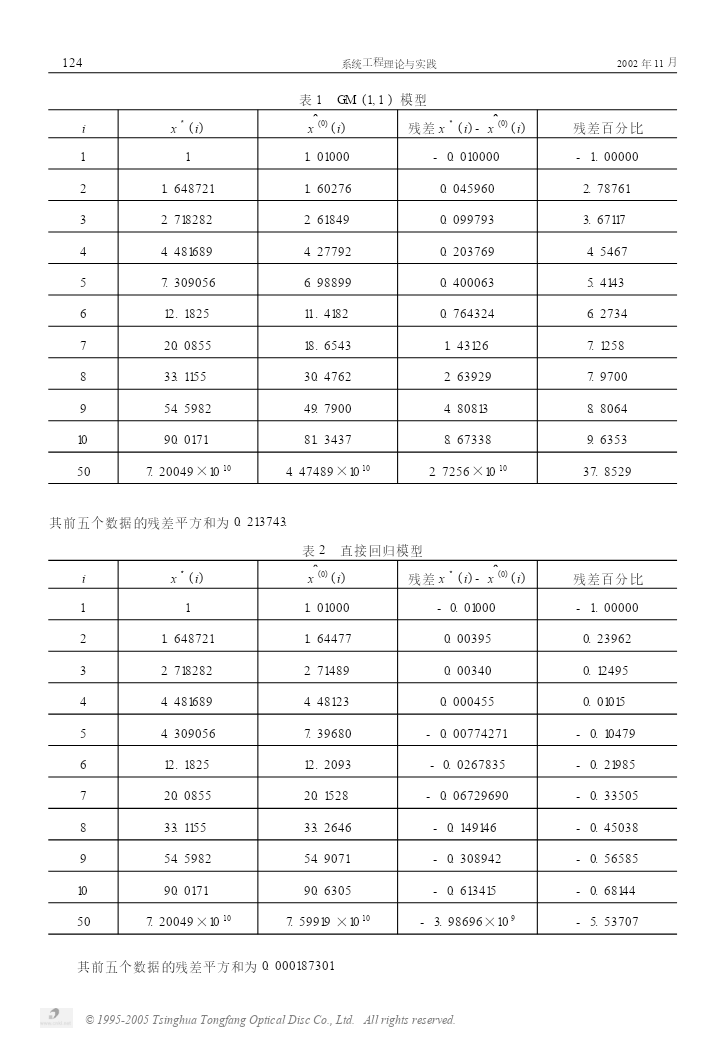
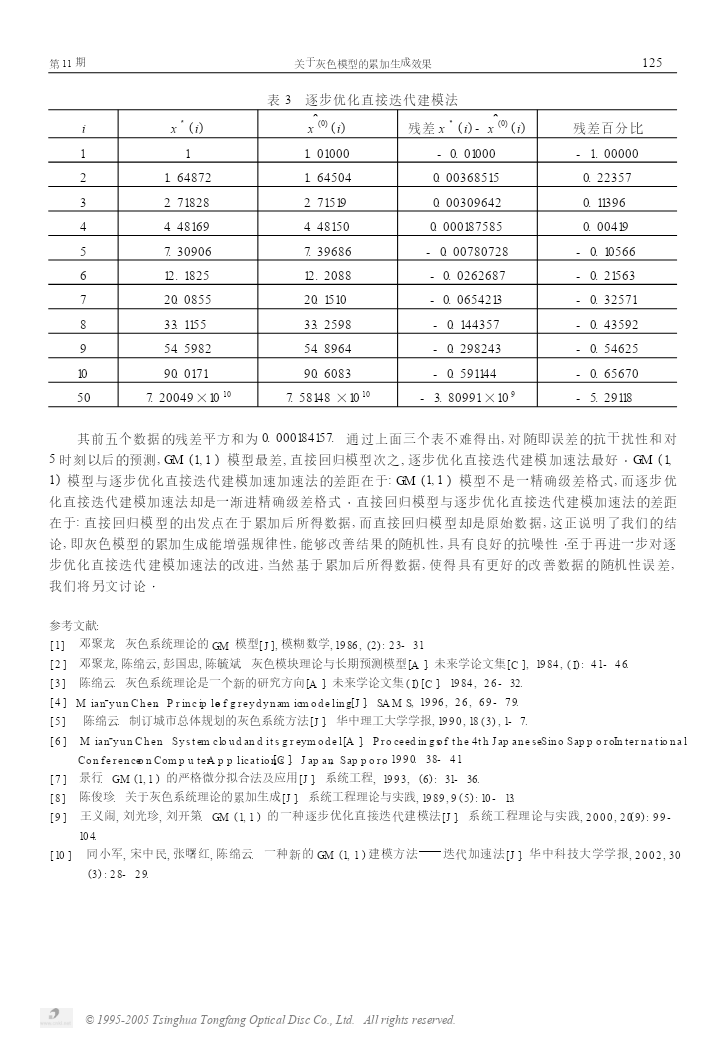
2002年11月系统工程理论与实践第11期

文章编号:100026788(2002)1120121205

关于灰色模型的累加生成效果

同小军1,2,陈绵云1,周龙3
(1.华中科技大学控制系,湖北武汉430074;2.石油大学应用数学系,山东东营257062;3.武汉工业学院电气系,湖北
武汉430021)

摘要:基于GM(1,1)灰色模型的理论背景,以级差格式探讨了GM(1,1)模型精度,研究结果表明,灰
色模型的累加生成能“增强”规律性,可改善结果的随机性,具有良好的抗噪性L
关键词:累加生成;灰色模型;级差格式;贫信息
中图分类号:O159文献标识码:A

OnAGOEffectoftheGreyModel

TONGXiao2jun1,2,CHENMian2yun1,ZHOULong3
(1.DepartmentofControlScienceandEngineering,HuazhongUniversityofScienceandTechnology,Wuhan430074,
China;2.DepartmentofMathematics,UniversityofPetroleum,Dongying257062,China;3.ElectricalandInformation
EngineeringDepartment,WuhanPolytechnicUniversity,Wuhan430021,China)

Abstract:InthefoundationofbackgroundoftheoryofthegreymodelGM(1,1),byuseofthegrade
differenceformat,discussmodelaccuracyofthegreymodelGM(1,1).TheresultofstudyisthatAc2
cumulatedGeneratingOperation(AGO)ofthegreymodelcan"strengthen"thelaw,canreformran2
domicityofnumbers,soithasniceanti2interferece.
Keywords:thegreymodel;thegradedifferenceformat;poorinformation

1引言
灰色系统理论自1982年问世以来,研究工作取得了很大的进展,已成功地应用于很多领域L灰色系统
理论的模型GM(1,1)[1]是最早应用也是迄今最为广泛应用的灰色模型,于1983年问世L1983年12月1
-5日,中国未来研究会主办的全国预测理论与技术方法学术讨论会在厦门市举行,会上发表的“灰色模
块理论与长期预测模型”[2]和“灰色系统理论是一个新的研究方向”[3]两篇论文,标志着GM(1,1)模型、灰
色量概念等从此诞生,翻开了一种独特的系统建模篇章的第一页L
GM(1,1)模型是在给定时序的生成层次(类加生成)上用灰色微分拟合方法建立的一阶单变量常系
数微分方程,适于描述一个环境相对不变的广义能量系统,因而是适用于预测的灰色模型,是灰色预测的
一种基本模型LGM(1,1)预测效果,许多情况下良好,有时甚佳,但预测实践表明,有时出现很大偏差,甚
至完全失效L究其原因,GM(1,1)存在着指数型发散误差源,响应函数指数系数越大,误差越大[4]L1990年
问世的按灰色动态建立的SCGM(1,n)模型[5-7],即系统云灰色模型,已克服了这类问题,并扩展了灰色
预测的应用范围L不少灰色系统研究者为提高GM(1,1)模型本身精度,对GM(1,1)本身作了大量有价值
的改进工作[7-10],取得了可喜进展L不同观点是也有的L灰色系统属于“贫”信息系统L描述灰色系统的
dx
GM(1,1)模型的背景方程是一阶单变量常系数微分方程ax=u,其中a,u是未知的常数Z如何将其化
dt
为一级差格式,并且由该级差格式得到的解a,u与真值误差较小?我们不妨回顾一下微分方程与差分方

收稿日期:2001201208
资助项目:国家自然科学基金(79970025,69874018);国防科技预研基金(OOJ15.3.JWO528)
作者简介:同小军(1967-),男,陕西富平人,副教授,博士生,主要从事偏微方程,模糊与灰色系统的理论与应用研究

©1995-2005TsinghuaTongfangOpticalDiscCo.,Ltd.Allrightsreserved.
221系统工程理论与实践2002年11月

程的关系Z每一个微分方程可对应多个差分方程,不同的差分方程其截断误差一般是不同的,但只要步长
h→0,应该有差分方程的解收敛于微分方程的解Z从而,类似地,对于灰微分方程所对应的级差格式也可
以不